Assumptions Of Linear Regression Analysis

Heb je je ooit afgevraagd hoe data scientists voorspellingen doen? Eén van de meest gebruikte tools in hun arsenaal is lineaire regressie. Het is een krachtige techniek, maar ze werkt alleen goed als bepaalde aannames kloppen. Wat gebeurt er als die aannames niet opgaan? Dat is wat we vandaag gaan ontrafelen.
Wat is Lineaire Regressie en Waarom Aannames Belangrijk Zijn
Lineaire regressie is in de kern een poging om een rechte lijn te vinden die de relatie tussen een onafhankelijke variabele (de voorspeller) en een afhankelijke variabele (de uitkomst) het beste beschrijft. Stel je voor dat je de relatie tussen het aantal uren studeren en het cijfer op een tentamen wilt onderzoeken. Lineaire regressie kan je helpen om die relatie te kwantificeren.
Maar hier komt de crux: deze techniek is gebaseerd op een aantal cruciale aannames. Als deze aannames worden geschonden, kunnen de resultaten misleidend of zelfs volledig fout zijn. Zie het als het bouwen van een huis: je hebt een stevige fundering nodig. De aannames van lineaire regressie zijn de fundering.
De Aannames Onder de Loep
1. Lineariteit: De Relatie Moet Lineair Zijn
Dit is misschien wel de meest voor de hand liggende aanname: de relatie tussen de onafhankelijke en afhankelijke variabele moet lineair zijn. Dit betekent dat een rechte lijn een goede benadering is van de data.
Hoe weet je of je data lineair is? Een scatterplot is je beste vriend. Maak een grafiek van je onafhankelijke variabele tegenover je afhankelijke variabele. Zie je een duidelijke kromme in de data? Dan is lineariteit waarschijnlijk geschonden. Je kunt dan overwegen om de variabelen te transformeren (bijvoorbeeld door de logaritme te nemen) of om een ander model te gebruiken (bijvoorbeeld een polynomiale regressie).
2. Onafhankelijkheid van Residuen: Geen Patronen in de Fouten
Dit betekent dat de fouten (het verschil tussen de werkelijke waarde en de voorspelde waarde) niet gecorreleerd mogen zijn met elkaar. Met andere woorden, de fout van één observatie mag geen invloed hebben op de fout van een andere observatie.
Waarom is dit belangrijk? Als de fouten gecorreleerd zijn, betekent dit dat er informatie in de fouten zit die het model niet heeft opgepikt. Dit kan leiden tot verkeerde schattingen van de parameters en onbetrouwbare voorspellingen.
Hoe kun je de onafhankelijkheid van residuen testen? Je kunt de Durbin-Watson test gebruiken. Een waarde rond de 2 duidt op onafhankelijkheid. Daarnaast kun je ook een plot van de residuen tegenover de voorspelde waarden maken. Zie je patronen (bijvoorbeeld een trechtervorm)? Dan is er waarschijnlijk sprake van autocorrelatie.
3. Homoscedasticiteit: Constante Variantie van de Fouten
Homoscedasticiteit is een moeilijk woord, maar het betekent simpelweg dat de variantie van de fouten constant moet zijn over alle niveaus van de onafhankelijke variabele. Anders gezegd, de spreiding van de fouten rond de regressielijn moet gelijk zijn voor alle waarden van de onafhankelijke variabele.
Wat gebeurt er als je heteroscedasticiteit hebt? Je standaardfouten worden verkeerd geschat, wat kan leiden tot onbetrouwbare significantietests en onnauwkeurige betrouwbaarheidsintervallen. Je model geeft dus minder precieze resultaten.
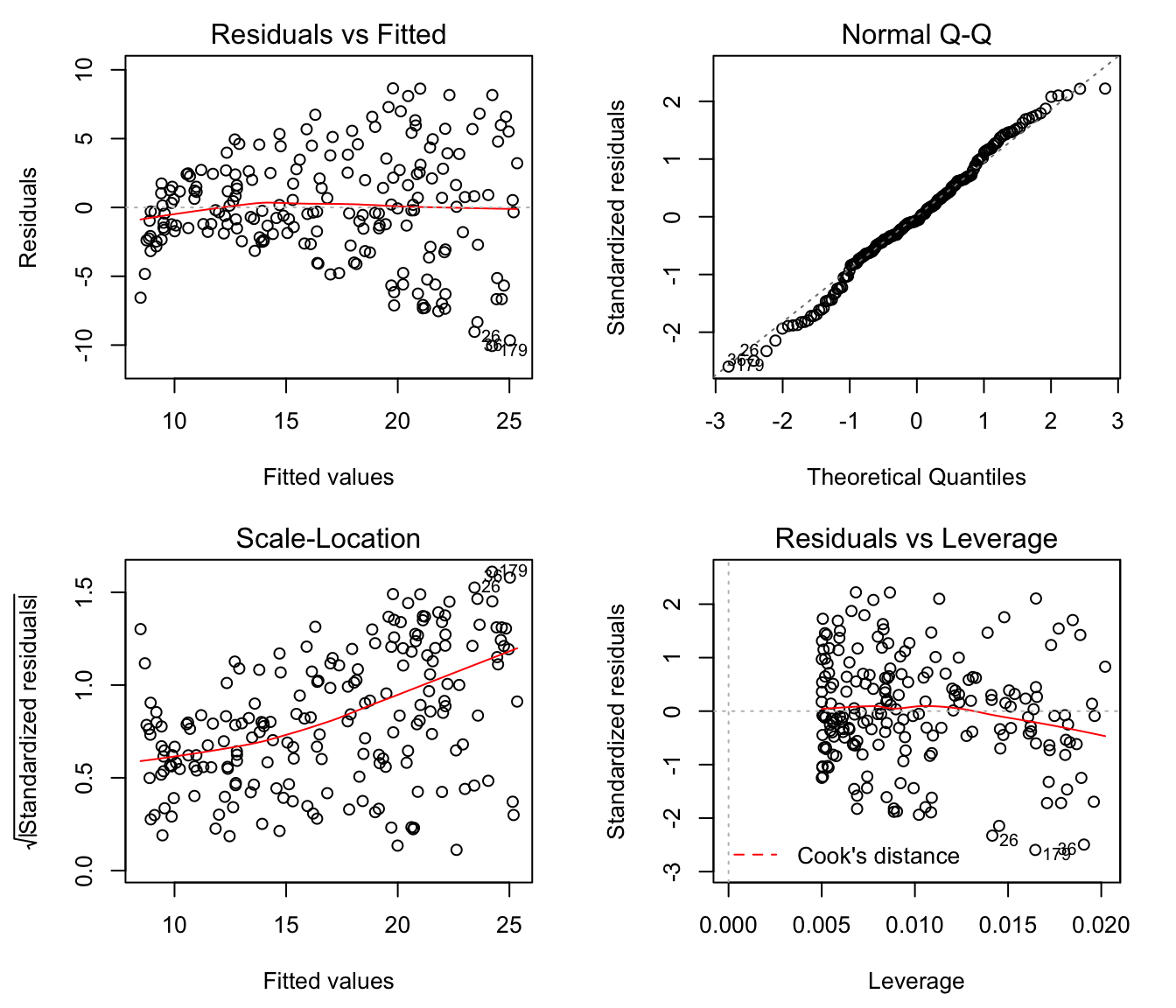
Hoe kun je heteroscedasticiteit opsporen? Net als bij de onafhankelijkheid van residuen is een plot van de residuen tegenover de voorspelde waarden erg handig. Als je een trechtervorm ziet (de spreiding van de fouten neemt toe of af naarmate de voorspelde waarde toeneemt), dan is er sprake van heteroscedasticiteit. Je kunt ook de Breusch-Pagan test of de White test gebruiken.
4. Normaliteit van Residuen: Fouten Moeten Normaal Verdeeld Zijn
De residuen (de fouten) moeten ongeveer normaal verdeeld zijn. Dit betekent dat de frequentieverdeling van de fouten een klokvormige curve moet benaderen.
Waarom is normaliteit belangrijk? Veel statistische tests (zoals de t-test en de F-test) die gebruikt worden om de significantie van de regressiecoëfficiënten te beoordelen, zijn gebaseerd op de aanname van normaliteit. Als de residuen niet normaal verdeeld zijn, kunnen deze tests ongeldig zijn.
Hoe kun je de normaliteit van residuen testen? Je kunt een histogram van de residuen maken en kijken of het een klokvormige curve benadert. Een formelere test is de Shapiro-Wilk test of de Kolmogorov-Smirnov test. Een Q-Q plot (Quantile-Quantile plot) is ook een krachtige tool. Als de residuen normaal verdeeld zijn, zullen de punten op de Q-Q plot dicht bij een rechte lijn liggen.
5. Geen Multicollineariteit: Onafhankelijke Variabelen Mogen Niet Sterk Gecorreleerd Zijn
Als je meerdere onafhankelijke variabelen hebt, mogen deze niet te sterk gecorreleerd zijn met elkaar. Dit wordt multicollineariteit genoemd.
Waarom is multicollineariteit een probleem? Het maakt het moeilijk om de individuele effecten van de onafhankelijke variabelen op de afhankelijke variabele te onderscheiden. De regressiecoëfficiënten worden onstabiel en moeilijk te interpreteren. Je kunt bijvoorbeeld een coëfficiënt vinden die significant is, maar het omgekeerde teken heeft van wat je zou verwachten.
Hoe kun je multicollineariteit opsporen? Je kunt de correlatie tussen de onafhankelijke variabelen berekenen. Een correlatiecoëfficiënt van dicht bij 1 of -1 duidt op een sterke correlatie. Een andere indicator is de Variance Inflation Factor (VIF). Een VIF van boven de 5 of 10 wordt vaak als indicatie gezien van multicollineariteit.
Wat Te Doen Als Aannames Geschonden Worden
Dus, je hebt ontdekt dat één of meerdere aannames van lineaire regressie niet opgaan voor jouw data. Geen paniek! Er zijn verschillende manieren om hiermee om te gaan:
- Transformeer je data: Soms kan het transformeren van de variabelen (bijvoorbeeld door de logaritme te nemen, de wortel te trekken of een machtsverheffing toe te passen) helpen om de aannames van lineariteit, homoscedasticiteit en normaliteit te vervullen.
- Gebruik een ander model: Als lineaire regressie niet geschikt is voor jouw data, kun je overwegen om een ander model te gebruiken, zoals polynomiale regressie, logistische regressie (als je afhankelijke variabele binair is) of niet-parametrische regressie.
- Gebruik robuuste regressie: Robuuste regressie is minder gevoelig voor uitschieters en schendingen van de aannames van normaliteit en homoscedasticiteit.
- Gebruik gewogen kleinste kwadraten (Weighted Least Squares): Als je heteroscedasticiteit hebt, kun je gewogen kleinste kwadraten gebruiken om de waarnemingen met een grotere variantie minder gewicht te geven.
- Verwijder uitschieters: Uitschieters kunnen een grote invloed hebben op de resultaten van lineaire regressie. Het is belangrijk om uitschieters te identificeren en te onderzoeken. Soms is het gerechtvaardigd om ze te verwijderen, maar dit moet altijd zorgvuldig overwogen worden.
Conclusie
Lineaire regressie is een krachtige tool, maar het is essentieel om de aannames te begrijpen en te controleren of ze opgaan voor jouw data. Als de aannames worden geschonden, zijn er verschillende manieren om hiermee om te gaan. Door kritisch naar je data te kijken en de juiste technieken te gebruiken, kun je ervoor zorgen dat je de juiste conclusies trekt en betrouwbare voorspellingen maakt. Onthoud: kennis is macht, vooral in de wereld van data analyse!

Bekijk ook deze gerelateerde berichten:
- Wat Ligt Er Aan De Andere Kant Van De Wereld
- Bol.com Winkel In De Buurt
- Primaire Secundaire En Tertiaire Preventie
- 8 Dagen Gestopt Met Roken
- Versvoet 2 Lettergrepen Een Onbeklemtoonde Gevolgd Door Een Beklemtoonde
- De Striphelden Suske En Wiske Waren Niet Altijd Samen
- Vlindernaald Doorspoelen Met Nacl Vilans
- Zat Afgestompt Met Een Boek In Laag Water 5 Letters
- Boek De Brief Voor De Koning
- Wanneer Kan Je Zorgtoeslag Aanvragen
