Multiple Regression Analysis Interpretation Spss

Herken je dat gevoel? Je hebt een hoop data verzameld, bent aan de slag gegaan met SPSS, en bent er nu achter dat je een heleboel getallen hebt die je eigenlijk niet goed kunt interpreteren. Je bent niet de enige! Multiple regressieanalyse is een krachtige tool, maar de interpretatie van de resultaten kan best lastig zijn. Laten we samen eens kijken hoe je de output van SPSS kunt ontcijferen en er daadwerkelijk *bruikbare* informatie uit kunt halen.

Wat is Multiple Regressieanalyse en Waarom Zou Je Het Gebruiken?

Multiple regressieanalyse is een statistische techniek die je helpt te begrijpen hoe meerdere onafhankelijke variabelen (ook wel predictoren genoemd) een afhankelijke variabele (de variabele die je wilt voorspellen of verklaren) beïnvloeden. Denk bijvoorbeeld aan: Hoe beïnvloeden leeftijd, opleidingsniveau en aantal jaren werkervaring iemands salaris?

Het is in feite een uitbreiding van simpele lineaire regressie (waarbij je slechts één predictor hebt), maar dan veel *krachtiger* omdat het rekening houdt met de complexe interacties tussen verschillende factoren. Gebruik multiple regressieanalyse als je:

• Wilt weten welke factoren de belangrijkste voorspellers zijn van een bepaalde uitkomst.
• Wilt voorspellen hoe de afhankelijke variabele verandert als je de waarden van de onafhankelijke variabelen verandert.
• Wilt controleren voor de effecten van confounders (variabelen die het verband tussen de predictoren en de afhankelijke variabele kunnen verstoren).

SPSS Output: Een Overzicht van de Belangrijkste Tabellen

SPSS geeft je een hoop output, maar niet alles is even belangrijk. Hier zijn de tabellen waar je je op moet focussen:

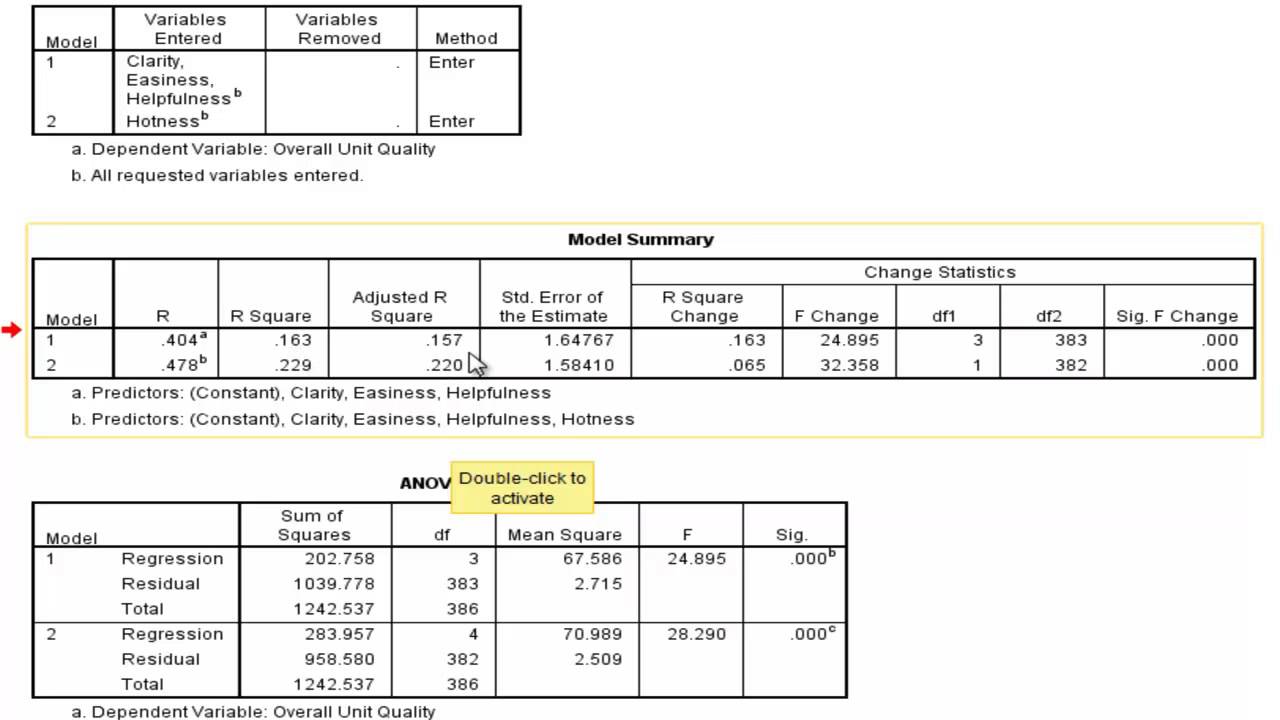
1. Model Summary

Deze tabel geeft je inzicht in hoe goed je model in zijn geheel presteert. Let vooral op:

• R: De multiple correlatiecoëfficiënt. Dit geeft aan hoe sterk de correlatie is tussen de voorspelde waarden en de geobserveerde waarden van de afhankelijke variabele. Een waarde dichtbij 1 geeft een sterke correlatie aan.
• R Square: De determinatiecoëfficiënt. Dit geeft aan *hoeveel* van de variantie in de afhankelijke variabele verklaard wordt door je model. Bijvoorbeeld, een R Square van 0.60 betekent dat 60% van de variatie in je afhankelijke variabele verklaard wordt door de onafhankelijke variabelen in je model.
• Adjusted R Square: Een aangepaste versie van R Square die rekening houdt met het aantal predictoren in je model. Gebruik deze waarde om de verklaringskracht van je model te beoordelen, vooral als je veel predictoren hebt. Het is een *meer accurate* maatstaf dan R Square, omdat het penaliseert voor het toevoegen van irrelevante predictoren.
• Std. Error of the Estimate: Een maat voor de gemiddelde grootte van de voorspellingsfouten. Hoe kleiner deze waarde, hoe nauwkeuriger je voorspellingen zijn.

Tip: Een hoge R Square is fijn, maar het is belangrijk om te onthouden dat correlatie geen causaliteit bewijst! Er kunnen andere factoren in het spel zijn die je niet hebt meegenomen in je model.

2. ANOVA (Analysis of Variance)

Deze tabel test de *overall* significantie van je model. Met andere woorden: verklaart je model significant meer variantie in de afhankelijke variabele dan je zou verwachten op basis van toeval?

• F-statistiek: Een teststatistiek die de variantie verklaard door je model vergelijkt met de variantie die niet verklaard wordt.
• Sig. (Significantie): De p-waarde die hoort bij de F-statistiek. Als deze waarde kleiner is dan je significantieniveau (meestal 0.05), dan is je model significant en verklaart het significant meer variantie dan je zou verwachten op basis van toeval.

Belangrijk: Als de ANOVA tabel niet significant is, dan is je *hele* model niet significant en kun je stoppen met interpreteren. De individuele predictoren zijn dan ook niet significant.

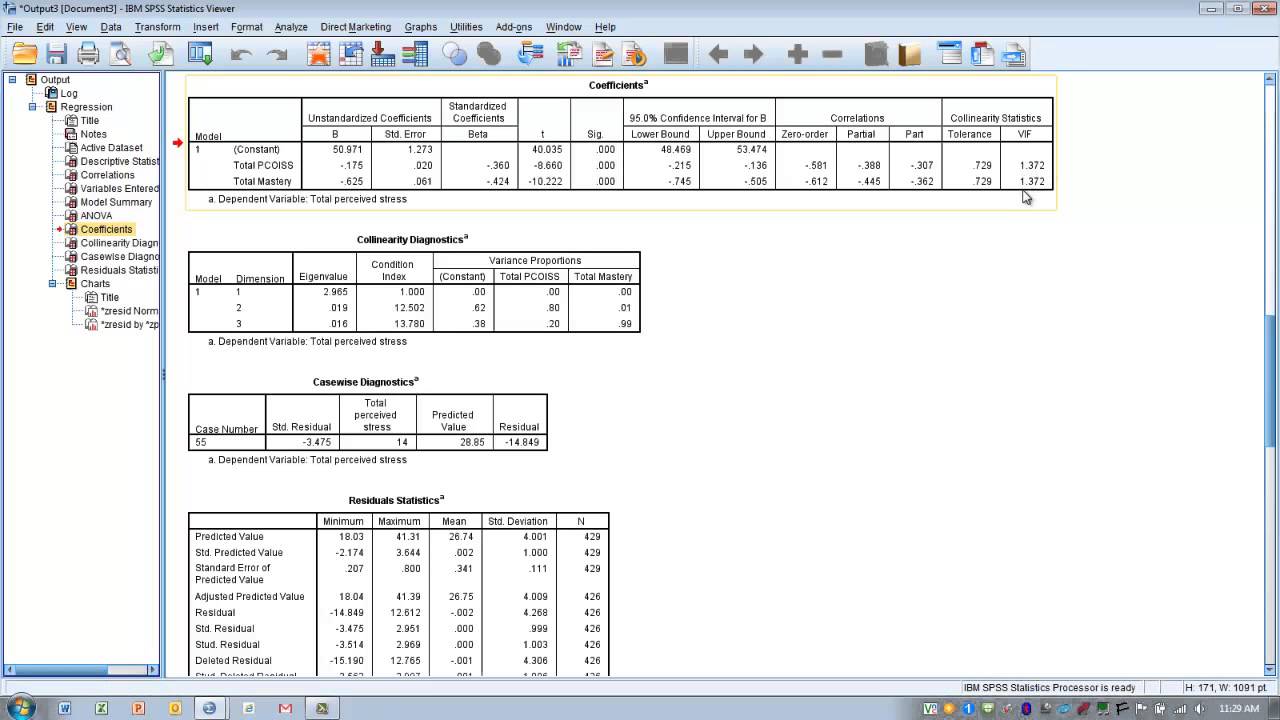
3. Coefficients

Dit is de belangrijkste tabel voor het interpreteren van de effecten van de individuele predictoren. Hier vind je:

• B (Unstandardized Coefficients): Dit zijn de regressiecoëfficiënten. Ze geven aan hoeveel de afhankelijke variabele verandert voor elke éénheid verandering in de predictor, *terwijl alle andere predictoren constant worden gehouden*.
  • Een positieve B betekent dat de afhankelijke variabele toeneemt als de predictor toeneemt.
  • Een negatieve B betekent dat de afhankelijke variabele afneemt als de predictor toeneemt.
  • Voorbeeld: Als de B voor "aantal jaren werkervaring" 2000 is, betekent dit dat, *gegeven dezelfde leeftijd en opleidingsniveau*, iemand met één jaar meer werkervaring gemiddeld €2000 meer verdient.
• Std. Error: De standaardfout van de regressiecoëfficiënt. Dit geeft aan hoe nauwkeurig de schatting van de B is.
• Beta (Standardized Coefficients): Dit zijn de gestandaardiseerde regressiecoëfficiënten. Ze geven aan hoe belangrijk de predictor is in verhouding tot de andere predictoren. Ze zijn handig om de *relatieve* belangrijkheid van de predictoren te vergelijken.
  • Je kunt de Beta’s direct vergelijken, omdat ze allemaal op dezelfde schaal staan. Hoe groter de absolute waarde van de Beta, hoe belangrijker de predictor.
• t: Een teststatistiek die test of de B significant afwijkt van nul.
• Sig. (Significantie): De p-waarde die hoort bij de t-statistiek. Als deze waarde kleiner is dan je significantieniveau (meestal 0.05), dan is de predictor significant en heeft het een significant effect op de afhankelijke variabele.

Let op: Je moet de B’s interpreteren in de context van de *andere* predictoren in je model. Het effect van een predictor kan veranderen als je andere predictoren toevoegt of verwijdert.

Collinearity Diagnostics

Het is belangrijk om de aanwezigheid van multicollineariteit te controleren. Multicollineariteit treedt op wanneer predictoren sterk gecorreleerd zijn met elkaar. Dit kan de schatting van de regressiecoëfficiënten vertekenen en de interpretatie bemoeilijken.

• Tolerance: Een waarde dichtbij 1 (maximaal) geeft aan dat er weinig collineariteit is. Waarden kleiner dan 0.2 duiden op een potentieel probleem.
• VIF (Variance Inflation Factor): Een waarde dichtbij 1 geeft aan dat er weinig collineariteit is. Waarden groter dan 5 of 10 duiden op een potentieel probleem.

Wat te doen bij multicollineariteit? Je kunt de sterk gecorreleerde predictoren verwijderen of ze combineren tot een nieuwe variabele.

Een Praktisch Voorbeeld

Stel, je wilt onderzoeken welke factoren de klanttevredenheid beïnvloeden. Je hebt de volgende predictoren:

• Wachttijd (in minuten): Hoe lang de klant moest wachten.
• Servicekwaliteit (schaal van 1 tot 5): Beoordeling van de service.
• Prijs (in euro’s): De prijs van het product of de dienst.

Na het uitvoeren van de multiple regressieanalyse in SPSS, vind je de volgende resultaten in de Coefficients tabel:

• Wachttijd: B = -0.2, Sig. = 0.01
• Servicekwaliteit: B = 0.8, Sig. = 0.001
• Prijs: B = -0.01, Sig. = 0.5

Interpretatie:

• Wachttijd: Elke minuut langer wachten leidt tot een *significante* afname van 0.2 punten in de klanttevredenheid, *gegeven dezelfde servicekwaliteit en prijs*.
• Servicekwaliteit: Elke punt hogere score op servicekwaliteit leidt tot een *significante* toename van 0.8 punten in de klanttevredenheid, *gegeven dezelfde wachttijd en prijs*.
• Prijs: De prijs heeft *geen significant* effect op de klanttevredenheid.

Actie: Op basis van deze resultaten kun je focussen op het verbeteren van de servicekwaliteit en het verkorten van de wachttijd om de klanttevredenheid te verhogen. De prijs lijkt minder belangrijk in dit geval.

Tot Slot: Blijf Oefenen en Experimenteren!

De interpretatie van multiple regressieanalyse is een vaardigheid die je ontwikkelt door te oefenen en te experimenteren. Probeer verschillende modellen uit, speel met de variabelen, en lees de output zorgvuldig. Hoe meer je oefent, hoe beter je wordt! En onthoud: als je er echt niet uitkomt, zoek dan hulp bij een statisticus of een ervaren SPSS gebruiker.

Veel succes!