Driehoek Berekenen Met 1 Zijde En 1 Hoek

Heb je je ooit afgevraagd hoe je een driehoek kunt berekenen als je slechts één zijde en één hoek kent? Je bent niet de enige! Veel leerlingen en professionals worstelen hiermee. Het lijkt misschien ingewikkeld, maar met de juiste kennis en tools is het absoluut te doen. Laten we samen diepduiken in de wereld van de trigonometrie en ontdekken hoe je deze uitdaging kunt overwinnen.

Waarom is dit belangrijk?

Het berekenen van driehoeken met beperkte informatie is niet alleen een theoretische oefening. Het komt in talloze praktische situaties voor, bijvoorbeeld in de architectuur, de landmeetkunde, de navigatie en zelfs in de videospelontwikkeling. Stel je voor dat je een toren wilt bouwen en je moet de lengte van een schaduw berekenen op basis van de hoogte van de toren en de hoek van de zon. Of je bent een landmeter die de oppervlakte van een onregelmatig stuk land moet bepalen. Kennis van trigonometrie is essentieel!

Volgens een onderzoek van de National Council of Teachers of Mathematics (NCTM) in de Verenigde Staten, is het toepassen van wiskundige concepten in realistische situaties cruciaal voor het ontwikkelen van een dieper begrip van wiskunde. Het berekenen van driehoeken is daar een perfect voorbeeld van.

De basisprincipes: Wat je moet weten

Voordat we aan de slag gaan met de methoden, is het belangrijk om de basisprincipes van trigonometrie te begrijpen:

Hoeken: Hoeken worden gemeten in graden (°) of radialen (rad). Een rechte hoek is 90° (π/2 rad).
Zijden: De zijden van een driehoek worden vaak aangeduid met kleine letters (a, b, c).
Sinus, Cosinus en Tangens (sin, cos, tan): Dit zijn trigonometrische functies die de verhouding tussen de zijden en hoeken van een rechthoekige driehoek beschrijven.
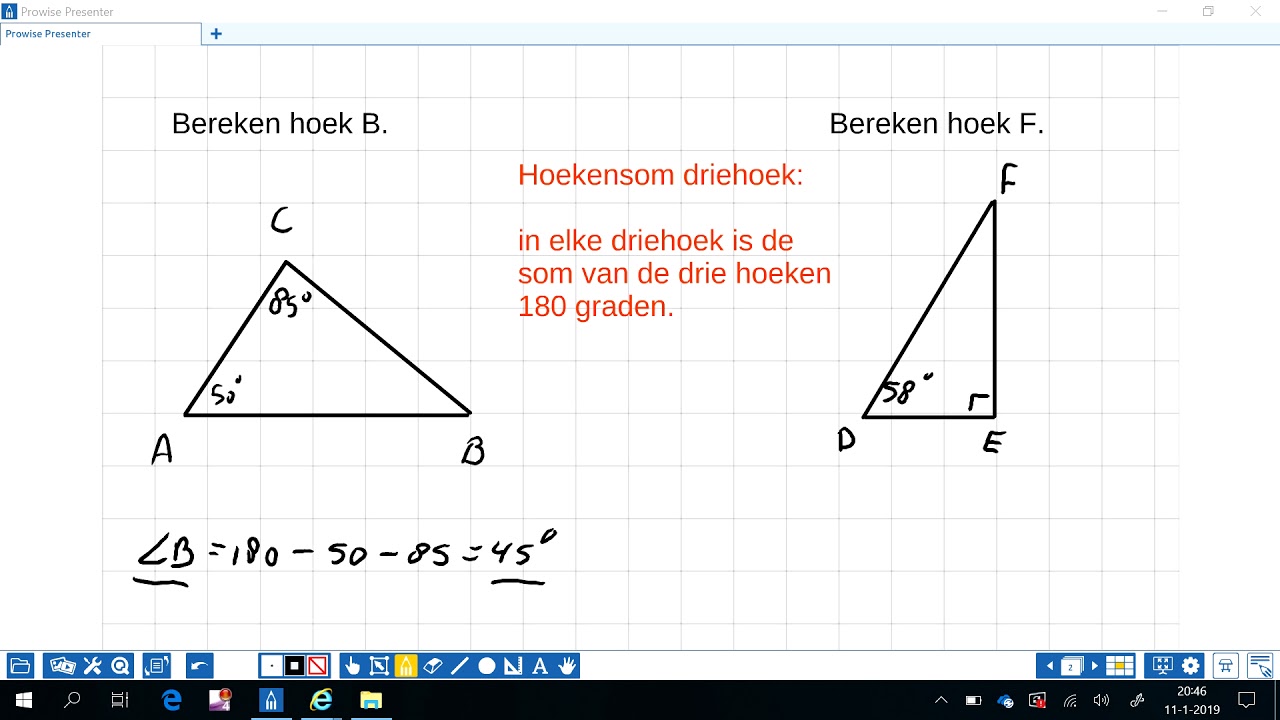
De som van de hoeken in een driehoek: De som van de hoeken in elke driehoek is altijd 180°.

Laten we focussen op een *rechthoekige* driehoek in eerste instantie. We hebben dan:

sin(hoek) = Overstaande zijde / Schuine zijde
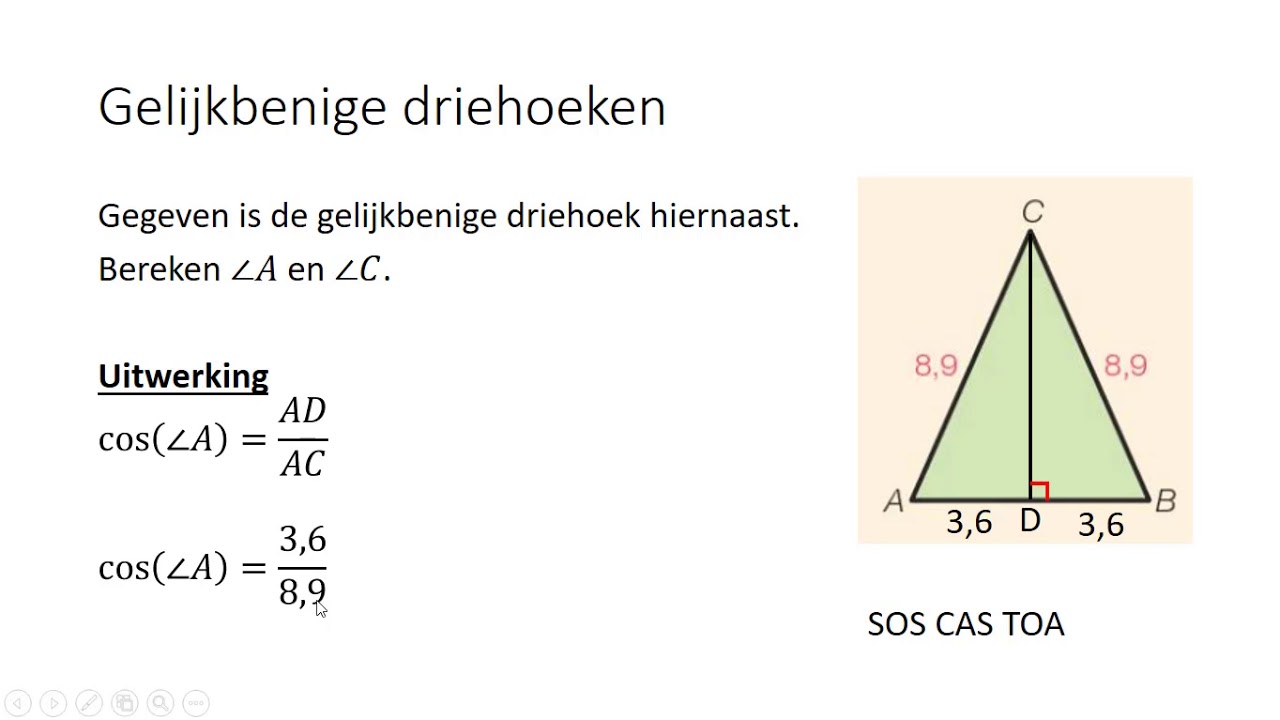
cos(hoek) = Aanliggende zijde / Schuine zijde
tan(hoek) = Overstaande zijde / Aanliggende zijde

Deze formules, vaak samengevat als *SOH CAH TOA*, zijn de sleutel tot het berekenen van de ontbrekende zijden en hoeken in een rechthoekige driehoek. Voor niet-rechthoekige driehoeken komen we later terug op de sinus- en cosinusregel.

Rechthoekige Driehoeken: Stap voor Stap

Laten we aannemen dat we een rechthoekige driehoek hebben met een zijde van 5 cm en een hoek van 30°. We willen de lengte van de andere zijden berekenen.

Identificeer wat je weet: We kennen een zijde (bijvoorbeeld de overstaande zijde) en een hoek (30°).
Kies de juiste trigonometrische functie: Als we de overstaande zijde kennen en de schuine zijde willen berekenen, gebruiken we de sinusfunctie (sin = Overstaande / Schuine).
Stel de vergelijking op: sin(30°) = 5 / Schuine zijde
Los de vergelijking op: Schuine zijde = 5 / sin(30°) = 5 / 0.5 = 10 cm
Bereken de resterende zijde: Nu kunnen we de stelling van Pythagoras gebruiken (a² + b² = c²) om de aanliggende zijde te berekenen: 5² + b² = 10² => b² = 100 - 25 = 75 => b = √75 ≈ 8.66 cm

Voorbeeld: Stel je voor dat je een ladder tegen een muur plaatst. De ladder is 4 meter lang en maakt een hoek van 60° met de grond. Hoe hoog reikt de ladder op de muur? We kunnen de sinus gebruiken: sin(60°) = Hoogte / 4 => Hoogte = 4 * sin(60°) ≈ 3.46 meter.

Niet-Rechthoekige Driehoeken: De Sinus- en Cosinusregel

Wat als de driehoek *niet* rechthoekig is? Dan kunnen we de sinus- en cosinusregel gebruiken.

Sinusregel: a/sin(A) = b/sin(B) = c/sin(C), waarbij a, b, en c de zijden zijn en A, B, en C de tegenoverliggende hoeken.
Cosinusregel: a² = b² + c² - 2bc * cos(A), b² = a² + c² - 2ac * cos(B), c² = a² + b² - 2ab * cos(C)

De sinusregel is handig wanneer je twee hoeken en een zijde kent (AAS) of twee zijden en een niet-ingesloten hoek (SSA). De cosinusregel is nuttig wanneer je drie zijden kent (SSS) of twee zijden en de ingesloten hoek (SAS).

Voorbeeld (sinusregel): Stel dat we een driehoek hebben met een zijde a = 8 cm, een hoek A = 45° en een hoek B = 60°. We willen de lengte van zijde b berekenen. Met de sinusregel: 8/sin(45°) = b/sin(60°) => b = (8 * sin(60°)) / sin(45°) ≈ 9.80 cm.

Voorbeeld (cosinusregel): Stel dat we een driehoek hebben met zijden a = 5 cm, b = 7 cm en de hoek C = 30°. We willen de lengte van zijde c berekenen. Met de cosinusregel: c² = 5² + 7² - 2 * 5 * 7 * cos(30°) => c² ≈ 14.88 => c ≈ 3.86 cm.

Tips & Tricks voor het Berekenen van Driehoeken

Maak een schets: Teken altijd een schets van de driehoek om een visueel overzicht te krijgen van de gegeven informatie.
Label de zijden en hoeken: Gebruik de juiste notatie (a, b, c voor zijden, A, B, C voor hoeken).
Kies de juiste formule: Bepaal of je de sinus, cosinus, tangens, sinusregel of cosinusregel moet gebruiken.
Wees nauwkeurig met je rekenmachine: Zorg ervoor dat je rekenmachine in de juiste modus staat (graden of radialen).
Controleer je antwoord: Kijk of je antwoord logisch is. Bijvoorbeeld, de langste zijde moet tegenover de grootste hoek liggen.
Online calculators: Maak gebruik van online driehoekscalculators om je antwoorden te controleren, maar *leer* de methodes erachter!

Veelgemaakte Fouten en Hoe Ze Te Vermijden

Het is gemakkelijk om fouten te maken bij het berekenen van driehoeken. Hier zijn enkele veelgemaakte fouten en hoe je ze kunt vermijden:

Verkeerde modus van de rekenmachine: Zorg ervoor dat je rekenmachine in de juiste modus staat (graden of radialen). Een veelvoorkomende fout is het gebruiken van graden wanneer radialen vereist zijn, of andersom.
Verkeerde formule kiezen: Gebruik de juiste trigonometrische functie of regel. Het is cruciaal om te weten welke informatie je hebt en welke formule daar het beste bij past.
Hoeken en zijden verwisselen: Let goed op welke hoek tegenover welke zijde ligt.
Rondingsfouten: Rond pas aan het einde van de berekening af om cumulatieve rondingsfouten te voorkomen.
Onjuiste invoer in de rekenmachine: Dubbelcheck altijd je invoer in de rekenmachine.

Conclusie

Het berekenen van driehoeken met één zijde en één hoek kan in eerste instantie intimiderend lijken, maar met de juiste kennis van trigonometrische functies en regels is het een beheersbare taak. Door de basisprincipes te begrijpen, de juiste formules te kiezen en nauwkeurig te werken, kun je de ontbrekende zijden en hoeken van een driehoek berekenen. Onthoud dat oefening kunst baart, dus pak een paar voorbeelden en begin met oefenen. Succes!

En vergeet niet, deze vaardigheden zijn niet alleen nuttig voor school of werk, maar ook voor alledaagse problemen. Dus, pak je rekenmachine en begin met meten!