Graden Van Een Driehoek Berekenen

Laten we eerlijk zijn, wiskunde kan soms aanvoelen als een doolhof. Je bent niet de enige als je je ooit hebt afgevraagd hoe je de hoeken van een driehoek berekent. Misschien zit je vast aan een huiswerkopdracht, probeer je een doe-het-zelf project nauwkeurig te bouwen, of ben je gewoon nieuwsgierig naar de principes achter geometrie. Wat je reden ook is, het is begrijpelijk dat je op zoek bent naar helderheid en een eenvoudige uitleg.

Dit artikel is er om je te helpen. We gaan de berekening van driehoekshoeken ontrafelen, en dat op een manier die hopelijk begrijpelijk en toepasbaar is, ongeacht je wiskundige achtergrond. We gaan de basisprincipes bekijken, verschillende scenario's behandelen en handige tips geven. En wees gerust, we houden het praktisch en relevant.

Wiskunde is niet alleen een academische oefening. Denk eens aan de architectuur van gebouwen, de constructie van bruggen, of zelfs het ontwerp van games. Driehoeken en hun hoeken spelen een cruciale rol in deze en talloze andere gebieden. Een onnauwkeurige hoekberekening kan leiden tot instabiliteit in een constructie, fouten in een ontwerp, of simpelweg een onjuiste snede in je houten plank voor je project. Kortom, het begrijpen van hoe je driehoekshoeken berekent, is een vaardigheid die je in veel verschillende situaties kan helpen.

De Basis: De Hoeken Som Regel

De basisregel die je moet kennen, is dat de som van de hoeken in een driehoek altijd 180 graden is. Dit is een fundamenteel principe dat je in staat stelt om de derde hoek te berekenen als je de andere twee kent. Laten we dit eens illustreren:

• Stel, je hebt een driehoek met hoeken van 60 en 80 graden.
• De som van deze twee hoeken is 60 + 80 = 140 graden.
• Om de derde hoek te vinden, trek je deze som af van 180: 180 - 140 = 40 graden.
• De derde hoek is dus 40 graden.

Dit werkt voor elke driehoek, ongeacht de vorm of grootte. Onthoud deze regel, en je bent al een heel eind!

Verschillende Soorten Driehoeken en Hun Berekeningen

Er bestaan verschillende soorten driehoeken, en elk type heeft zijn eigen specifieke eigenschappen die de berekening van de hoeken kunnen vereenvoudigen.

Gelijkzijdige Driehoeken

Een gelijkzijdige driehoek heeft drie gelijke zijden en drie gelijke hoeken. Aangezien de som van de hoeken 180 graden is, is elke hoek in een gelijkzijdige driehoek 180 / 3 = 60 graden. Dit is altijd het geval, dus je hoeft hier geen ingewikkelde berekeningen uit te voeren.

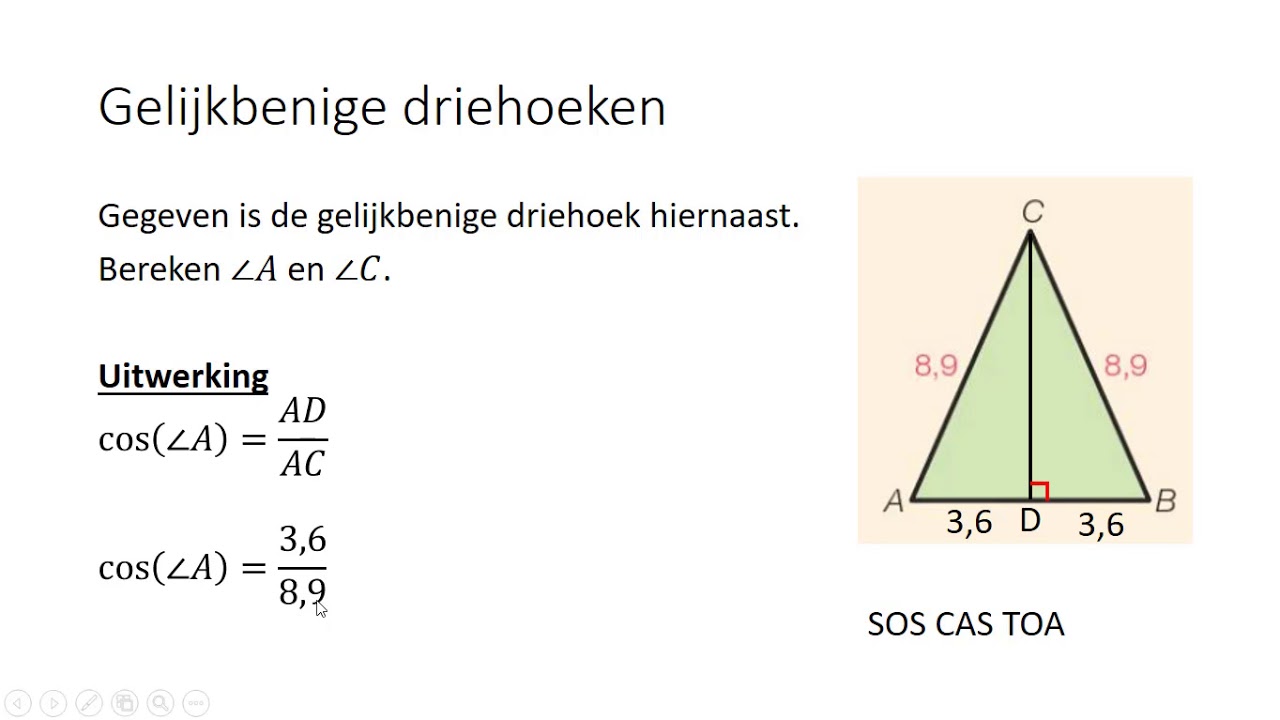
Gelijkbenige Driehoeken

Een gelijkbenige driehoek heeft twee gelijke zijden en twee gelijke hoeken. De gelijke hoeken bevinden zich tegenover de gelijke zijden. Als je de waarde van één van deze gelijke hoeken weet, weet je automatisch ook de waarde van de andere. Om de derde hoek te vinden, trek je de som van de twee gelijke hoeken af van 180 graden.

Voorbeeld: Stel, een gelijkbenige driehoek heeft twee hoeken van 70 graden. De derde hoek is dan 180 - (70 + 70) = 40 graden.

Rechthoekige Driehoeken

Een rechthoekige driehoek heeft één hoek van 90 graden (een rechte hoek). De zijde tegenover de rechte hoek wordt de hypotenusa genoemd. Als je één van de andere hoeken in een rechthoekige driehoek weet, kun je de derde hoek eenvoudig berekenen:

• Trek de bekende hoek af van 90 graden. (omdat de andere twee hoeken samen 90 graden moeten zijn)

Voorbeeld: Een rechthoekige driehoek heeft een hoek van 30 graden. De derde hoek is dan 90 - 30 = 60 graden.

Ongelijkzijdige Driehoeken

Een ongelijkzijdige driehoek (soms ook scalene genoemd) heeft drie ongelijke zijden en drie ongelijke hoeken. In dit geval kun je de hoeken niet direct berekenen op basis van één bekende hoek, behalve als je additionele informatie hebt (bijvoorbeeld de lengte van de zijden). In dat geval kun je de sinusregel of de cosinusregel gebruiken. Deze regels leggen een verband tussen de hoeken en de zijden van een driehoek.

De Sinus- en Cosinusregel

De sinus- en cosinusregels zijn krachtige hulpmiddelen voor het berekenen van hoeken en zijden in elke driehoek, niet alleen in rechthoekige driehoeken. Ze zijn vooral handig als je niet genoeg hoeken hebt om de 180-graden regel toe te passen.

De Sinusregel

De sinusregel stelt dat de verhouding tussen de lengte van een zijde en de sinus van de tegenoverliggende hoek constant is voor alle zijden en hoeken in een driehoek. Wiskundig gezien is dit:

a / sin(A) = b / sin(B) = c / sin(C)

Waar:

• a, b, c zijn de lengtes van de zijden van de driehoek.
• A, B, C zijn de hoeken tegenover respectievelijk de zijden a, b, c.

Als je bijvoorbeeld de lengte van twee zijden (a en b) en de hoek tegenover één van die zijden (A) kent, kun je de hoek tegenover de andere bekende zijde (B) berekenen:

sin(B) = (b * sin(A)) / a

B = arcsin((b * sin(A)) / a)

De arcsin functie (ook bekend als de inverse sinus of sin^-1) is de functie die de hoek geeft waarvan de sinus gelijk is aan de gegeven waarde. De meeste wetenschappelijke rekenmachines hebben een knop voor arcsin.

De Cosinusregel

De cosinusregel is een andere krachtige tool die een verband legt tussen de lengtes van de zijden van een driehoek en de cosinus van één van de hoeken. De meest voorkomende vorm van de cosinusregel is:

c² = a² + b² - 2ab * cos(C)

Waar:

• a, b, c zijn de lengtes van de zijden van de driehoek.
• C is de hoek tegenover de zijde c.

Als je de lengtes van alle drie de zijden (a, b, c) kent, kun je de hoek C berekenen:

cos(C) = (a² + b² - c²) / (2ab)

C = arccos((a² + b² - c²) / (2ab))

Net als bij de sinusregel, heb je een wetenschappelijke rekenmachine nodig om de arccos functie (de inverse cosinus of cos^-1) te gebruiken.

Veelgemaakte Fouten en Hoe Ze Te Vermijden

Bij het berekenen van driehoekshoeken, zijn er een paar veelvoorkomende fouten die je kunt maken. Hier zijn een paar tips om ze te vermijden:

• Verkeerde eenheden: Zorg ervoor dat je de juiste eenheden gebruikt. Hoeken worden meestal gemeten in graden. Als je rekenmachine is ingesteld op radialen, krijg je verkeerde antwoorden.
• Verkeerde rekenmachine-instellingen: Controleer de instellingen van je rekenmachine voordat je sinus, cosinus of inverse functies gebruikt.
• Afrondingsfouten: Rond getallen niet te vroeg af. Bewaar zoveel mogelijk decimalen tijdens de berekening en rond pas het eindresultaat af.
• Verkeerde interpretatie van de antwoorden van de arcsin functie: De arcsin functie geeft een hoek tussen -90 en 90 graden. Soms moet je de hoek aanpassen om de juiste hoek in de driehoek te krijgen (vooral in de goniometrie).
• Verkeerde toepassing van de sinus- of cosinusregel: Zorg ervoor dat je de regels correct toepast en de juiste zijden en hoeken gebruikt. Maak een schets van de driehoek om jezelf te helpen.

Waarom Dit Belangrijk Is

Hoewel het berekenen van driehoekshoeken misschien een abstract concept lijkt, heeft het relevante toepassingen in het dagelijks leven. Van navigatie (waarbij hoeken worden gebruikt om routes te bepalen) tot constructie (waarbij nauwkeurige hoeken cruciaal zijn voor stabiliteit), het begrijpen van deze principes is van onschatbare waarde. Ook in de kunst en vormgeving worden hoeken gebruikt om perspectief en evenwicht te creëren.

Sommigen beweren dat moderne technologie (zoals CAD-software) deze handmatige berekeningen overbodig maakt. Hoewel software tools absoluut nuttig zijn, is het belangrijk om de fundamentele principes te begrijpen die aan de basis liggen. Dit helpt je om de software effectiever te gebruiken en fouten te herkennen.

Conclusie

We hebben een reis gemaakt door de wereld van driehoekshoeken, beginnend met de basisregel van 180 graden, vervolgens verschillende soorten driehoeken onderzocht, en uiteindelijk de sinus- en cosinusregels ontdekt. We hebben ook gekeken naar veelgemaakte fouten en hoe je ze kunt vermijden. Hopelijk heb je nu een beter begrip van hoe je driehoekshoeken kunt berekenen.

Neem de tijd om deze principes te oefenen. Hoe meer je oefent, hoe beter je ze zult begrijpen.

Ben je klaar om je nieuw verworven kennis toe te passen op een echt project?