Hoe Bereken Je De Hoogte Van Een Driehoek

Laten we eerlijk zijn, wiskunde kan soms een doolhof zijn. Je zit daar, staart naar een driehoek en je vraagt je af: "Hoe bereken ik nu weer die hoogte?" Geen paniek! We zijn er allemaal geweest. Het is frustrerend wanneer een opgave die in theorie eenvoudig lijkt, in de praktijk een obstakel vormt. Misschien heb je de hoogte nodig voor een schoolopdracht, een DIY-project, of zelfs om de oppervlakte van een stuk grond te berekenen. Wat de reden ook is, dit artikel is er om je te helpen.

Dit is meer dan alleen theorie. Het berekenen van de hoogte van een driehoek is niet alleen relevant voor wiskundelessen. Stel je voor: je wilt een zeil maken voor je boot. Je hebt de vorm van een driehoek, maar je weet niet hoe je de benodigde hoeveelheid stof kunt berekenen. Zonder de hoogte van de driehoek is het lastig om de oppervlakte te bepalen en dus ook de hoeveelheid zeil dat je nodig hebt. Of denk aan een timmerman die een driehoekig dak construeert. De hoogte van de driehoek is cruciaal voor de stabiliteit en het ontwerp. Het is dus een praktische vaardigheid die in veel verschillende situaties van pas kan komen.

Sommigen zullen zeggen: "Waarom zou ik dit zelf doen? Er zijn toch online calculators voor?" Dat klopt, er zijn veel handige tools beschikbaar. Maar het is belangrijk om de principes achter de berekeningen te begrijpen. Een calculator geeft je alleen een antwoord, maar leert je niet de logica en redenering die erachter schuilgaat. Bovendien, wat als je geen internet hebt? Of als je de calculator niet vertrouwt? Het is altijd waardevol om de kennis zelf te bezitten.

Verschillende Soorten Driehoeken, Verschillende Aanpakken

Niet alle driehoeken zijn gelijk. De manier waarop je de hoogte berekent, hangt af van het type driehoek dat je voor je hebt.

Rechthoekige Driehoek

De rechthoekige driehoek is misschien wel de eenvoudigste. Een van de hoeken is 90 graden. In dit geval is een van de zijden (de zijde die aan de rechte hoek grenst) direct de hoogte, als je de andere zijde die aan de rechte hoek grenst als basis beschouwt.

Voorbeeld: Stel dat je een rechthoekige driehoek hebt waarbij de ene zijde aan de rechte hoek 3 cm is en de andere 4 cm. Als je de zijde van 4 cm als basis neemt, dan is de hoogte direct 3 cm.

Gelijkzijdige Driehoek

Een gelijkzijdige driehoek heeft drie gelijke zijden en drie gelijke hoeken (alle 60 graden). De hoogte van een gelijkzijdige driehoek kun je berekenen met de stelling van Pythagoras (zie hieronder) of met de volgende formule:

hoogte = (zijde / 2) * √3

Voorbeeld: Stel dat de zijde van de gelijkzijdige driehoek 6 cm is. Dan is de hoogte (6 / 2) * √3 = 3 * √3 ≈ 5.2 cm.

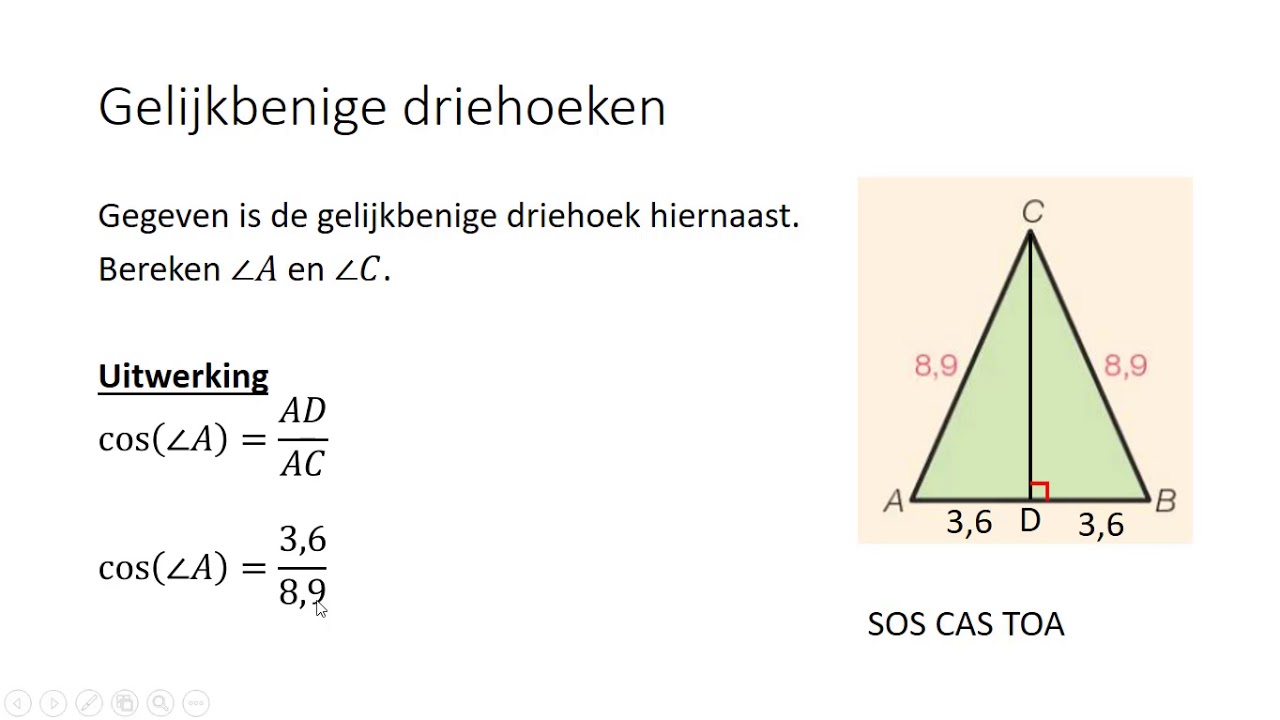
Gelijkbenige Driehoek

Een gelijkbenige driehoek heeft twee gelijke zijden. De hoogte is de lijn vanuit de top (de hoek tussen de twee gelijke zijden) loodrecht op de basis (de derde zijde). Deze hoogte deelt de basis in twee gelijke stukken. Om de hoogte te berekenen, kun je weer de stelling van Pythagoras gebruiken.

Ongelijkzijdige Driehoek

Een ongelijkzijdige driehoek heeft drie verschillende zijden. Hier wordt het iets complexer, maar geen zorgen, we komen er! Je kunt de hoogte op verschillende manieren berekenen, bijvoorbeeld met de formule van Heron (zie hieronder) of met behulp van trigonometrie (sinus, cosinus, tangens) als je een hoek weet.

De Stelling van Pythagoras: Een Onmisbare Tool

De stelling van Pythagoras is een fundamentele regel in de meetkunde. Ze stelt dat in een rechthoekige driehoek het kwadraat van de schuine zijde (de zijde tegenover de rechte hoek) gelijk is aan de som van de kwadraten van de andere twee zijden. In formulevorm: a² + b² = c²

Hoe gebruik je dit voor de hoogte? Je kunt de stelling van Pythagoras gebruiken om de hoogte van een gelijkbenige of ongelijkzijdige driehoek te berekenen door de driehoek in twee rechthoekige driehoeken te verdelen. Stel dat je de basis van de oorspronkelijke driehoek in twee gelijke stukken hebt verdeeld door de hoogte te tekenen. Nu heb je een rechthoekige driehoek. Je kent de lengte van de schuine zijde (een van de oorspronkelijke zijden van de driehoek) en de lengte van de halve basis. Je kunt nu de stelling van Pythagoras gebruiken om de hoogte te berekenen.

Voorbeeld: Stel dat je een gelijkbenige driehoek hebt met zijden van 5 cm, 5 cm en 6 cm. De basis is dus 6 cm. De hoogte deelt de basis in twee stukken van 3 cm. Nu heb je een rechthoekige driehoek met een schuine zijde van 5 cm en een zijde van 3 cm. Dus: 3² + hoogte² = 5². Dus hoogte² = 5² - 3² = 25 - 9 = 16. Dus de hoogte = √16 = 4 cm.

De Formule van Heron: Voor de Ongelijkzijdige Driehoek

De formule van Heron is handig als je de lengtes van alle drie de zijden van een driehoek kent, maar geen hoeken. De formule ziet er als volgt uit:

Oppervlakte = √(s(s-a)(s-b)(s-c))

Waarbij:

a, b en c de lengtes van de zijden van de driehoek zijn
s de halve omtrek is: s = (a + b + c) / 2

Om de hoogte te berekenen, moet je eerst de oppervlakte berekenen met de formule van Heron. Daarna gebruik je de formule voor de oppervlakte van een driehoek (Oppervlakte = 1/2 * basis * hoogte) om de hoogte te vinden.

Voorbeeld: Stel dat je een driehoek hebt met zijden van 4 cm, 5 cm en 7 cm. Eerst bereken je de halve omtrek: s = (4 + 5 + 7) / 2 = 8 cm. Dan bereken je de oppervlakte: Oppervlakte = √(8(8-4)(8-5)(8-7)) = √(8 * 4 * 3 * 1) = √96 ≈ 9.8 cm². Stel dat je de zijde van 7 cm als basis neemt. Dan geldt: 9.8 = 1/2 * 7 * hoogte. Dus hoogte = (9.8 * 2) / 7 ≈ 2.8 cm.

Trigonometrie: Wanneer Je Hoeken Kent

Als je een hoek en de lengte van een zijde kent, kun je trigonometrie gebruiken om de hoogte te berekenen. De belangrijkste trigonometrische functies zijn sinus (sin), cosinus (cos) en tangens (tan).

Hoe gebruik je dit voor de hoogte? Als je een hoek kent die niet de rechte hoek is, en de lengte van de schuine zijde, dan kun je de sinus gebruiken: sin(hoek) = overstaande zijde / schuine zijde. De overstaande zijde is in dit geval de hoogte van de driehoek.

Voorbeeld: Stel dat je een driehoek hebt met een hoek van 30 graden en een schuine zijde van 10 cm. Dan geldt: sin(30°) = hoogte / 10. Sin(30°) = 0.5, dus 0.5 = hoogte / 10. Dus hoogte = 0.5 * 10 = 5 cm.

Stappenplan voor het Berekenen van de Hoogte

Laten we de stappen even samenvatten:

Identificeer het type driehoek: Is het een rechthoekige, gelijkzijdige, gelijkbenige of ongelijkzijdige driehoek?
Kijk welke informatie je hebt: Ken je de lengtes van de zijden? Ken je een hoek?
Kies de juiste methode:
- Rechthoekige driehoek: De hoogte is een van de zijden die aan de rechte hoek grenst.
- Gelijkzijdige driehoek: Gebruik de formule: hoogte = (zijde / 2) * √3
- Gelijkbenige driehoek: Gebruik de stelling van Pythagoras.
- Ongelijkzijdige driehoek: Gebruik de formule van Heron of trigonometrie.
Pas de formule toe en bereken de hoogte.
Controleer je antwoord: Is het antwoord logisch? Maak eventueel een schets van de driehoek om je te helpen.

Veelgemaakte Fouten en Hoe Ze te Vermijden

Het verkeerde type driehoek identificeren: Dit leidt tot het gebruik van de verkeerde formule.
De stelling van Pythagoras verkeerd toepassen: Zorg ervoor dat je de schuine zijde correct identificeert.
Vergeten de wortel te trekken: Als je de stelling van Pythagoras gebruikt, vergeet dan niet de wortel te trekken van het kwadraat van de hoogte.
De verkeerde eenheden gebruiken: Zorg ervoor dat alle lengtes in dezelfde eenheden zijn (bijvoorbeeld allemaal in centimeters).

Oefening Baart Kunst

Net als bij elke vaardigheid, wordt je beter in het berekenen van de hoogte van een driehoek door te oefenen. Zoek online oefeningen of bedenk zelf voorbeelden. Hoe meer je oefent, hoe sneller en gemakkelijker het wordt.

Voorbeeld Oefening: Je hebt een driehoek met zijden van 8 cm, 10 cm en 12 cm. Bereken de hoogte ten opzichte van de basis van 12 cm.

Antwoord: Gebruik de formule van Heron: s = (8 + 10 + 12) / 2 = 15. Oppervlakte = √(15(15-8)(15-10)(15-12)) = √(15 * 7 * 5 * 3) = √1575 ≈ 39.7 cm². Hoogte = (39.7 * 2) / 12 ≈ 6.6 cm.

Het berekenen van de hoogte van een driehoek lijkt misschien ingewikkeld, maar met de juiste kennis en oefening is het zeker te doen. Onthoud de verschillende soorten driehoeken, de stelling van Pythagoras, de formule van Heron en trigonometrie. Met deze tools in je gereedschapskist ben je klaar om elke driehoek aan te pakken!

Dus, ben je klaar om je wiskundige vaardigheden in de praktijk te brengen en zelf een paar driehoeken te berekenen?