Hoe Bereken Je De Omtrek Van Een Cirkel

Heb je je ooit afgevraagd hoe ze de afstand rond een pizza bepalen, of hoe ze ervoor zorgen dat een wiel perfect past? Het antwoord ligt in de simpele, maar krachtige formule voor het berekenen van de omtrek van een cirkel. Deze formule is niet alleen nuttig in de wiskunde, maar duikt overal om ons heen op, van de architectuur van gebouwen tot het ontwerp van fietswielen. In dit artikel duiken we in de wereld van cirkels en leggen we je stap voor stap uit hoe je de omtrek kunt berekenen. Geen ingewikkelde wiskundetaal, maar een heldere en praktische uitleg voor iedereen.

Wat is een cirkel en waarom is de omtrek belangrijk?

Laten we beginnen met de basis. Een cirkel is een perfect ronde vorm, waarbij alle punten op de rand dezelfde afstand hebben tot het middelpunt. Deze afstand noemen we de straal (r). De afstand van de ene kant van de cirkel naar de andere, dwars door het middelpunt, noemen we de diameter (d). De diameter is dus twee keer zo groot als de straal (d = 2r).

De omtrek van een cirkel is simpelweg de afstand rondom de cirkel. Het is de totale lengte van de rand. Waarom is dit belangrijk? Nou, denk eens aan de volgende situaties:

• Engineering en constructie: Bij het bouwen van bruggen, tunnels en andere constructies zijn precieze berekeningen van cirkelvormige elementen essentieel.
• Productontwerp: Of het nu gaat om het ontwerpen van wielen, pizza's of frisbees, de omtrek is een cruciale factor.
• Navigatie: De aarde is (bijna) een bol, dus cirkelberekeningen zijn belangrijk voor het bepalen van afstanden.
• Alledaagse situaties: Zelfs bij het afmeten van een taartvorm of het bepalen hoeveel lint je nodig hebt voor een cadeau is de omtrek relevant.

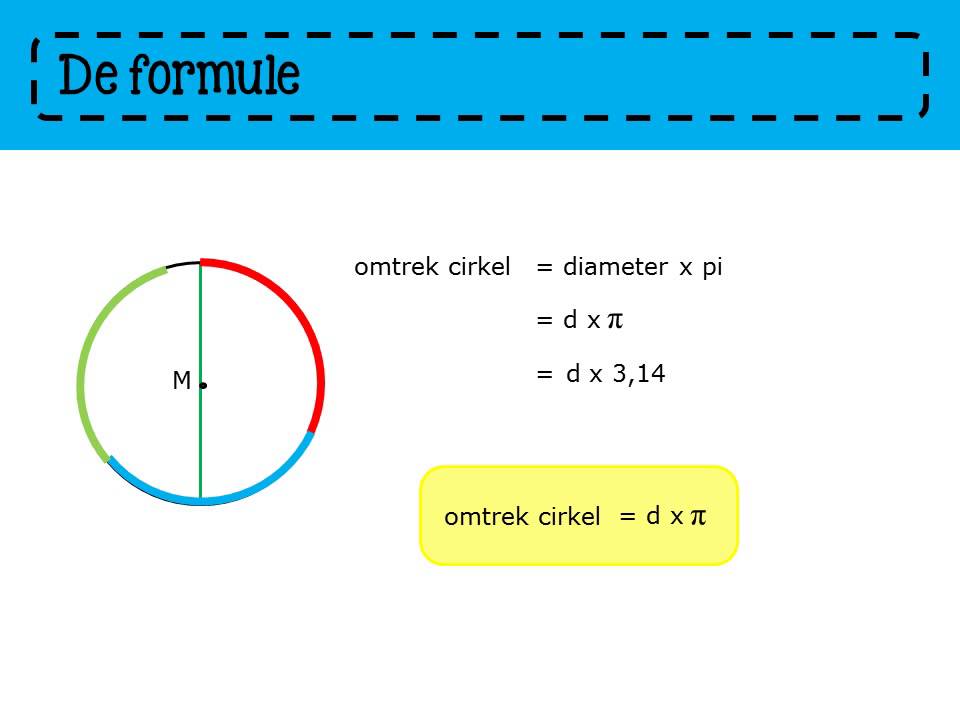
De magische formule: Omtrek = πd = 2πr

De omtrek van een cirkel kan worden berekend met een eenvoudige formule:

Omtrek = πd (pi maal de diameter)

of

Omtrek = 2πr (2 maal pi maal de straal)

Maar wat is π (pi) eigenlijk? Pi is een wiskundige constante, een irrationeel getal dat de verhouding weergeeft tussen de omtrek van een cirkel en zijn diameter. De waarde van pi is ongeveer 3,14159, maar voor de meeste berekeningen is 3,14 voldoende. Pi is oneindig en niet-repeterend, wat betekent dat de decimalen oneindig doorgaan zonder een vast patroon.

Een korte geschiedenis van Pi

De ontdekking en benadering van pi is een verhaal dat duizenden jaren teruggaat. De oude Babyloniërs en Egyptenaren kenden al benaderingen van pi. De Babyloniërs gebruikten een waarde van 3 1/8 (3,125), terwijl de Egyptenaren een waarde van ongeveer 3,16 gebruikten. De Griekse wiskundige Archimedes was een van de eersten die pi nauwkeurig berekende door middel van geometrische methoden. Hij bepaalde dat pi ergens tussen 3 1/7 en 3 10/71 lag. Later, in de middeleeuwen, werd pi verder verfijnd door wiskundigen in India en China. Vandaag de dag hebben computers pi berekend tot biljoenen decimalen, maar voor de meeste praktische toepassingen is 3,14 een prima benadering.

Stap voor stap: Hoe bereken je de omtrek?

Laten we nu kijken naar een paar voorbeelden om de formule in actie te zien:

Voorbeeld 1: Gegeven is de diameter

Stel, je hebt een pizza met een diameter van 30 cm. Wat is de omtrek van de pizza?

1. Identificeer de gegeven informatie: De diameter (d) is 30 cm.
2. Gebruik de formule: Omtrek = πd
3. Vul de waarde in: Omtrek = 3,14 * 30 cm
4. Bereken de omtrek: Omtrek = 94,2 cm

De omtrek van de pizza is dus ongeveer 94,2 cm.

Voorbeeld 2: Gegeven is de straal

Stel, je hebt een taartvorm met een straal van 15 cm. Wat is de omtrek van de taartvorm?

1. Identificeer de gegeven informatie: De straal (r) is 15 cm.
2. Gebruik de formule: Omtrek = 2πr
3. Vul de waarde in: Omtrek = 2 * 3,14 * 15 cm
4. Bereken de omtrek: Omtrek = 94,2 cm

De omtrek van de taartvorm is dus ook ongeveer 94,2 cm. Merk op dat we hetzelfde antwoord krijgen, omdat de diameter van de pizza in het vorige voorbeeld gelijk is aan twee keer de straal van de taartvorm.

Tips en trucs voor het berekenen van de omtrek

• Wees consistent met de eenheden: Zorg ervoor dat je dezelfde eenheden gebruikt voor de diameter/straal en de omtrek. Als de diameter in centimeters is, zal de omtrek ook in centimeters zijn.
• Gebruik een rekenmachine: Vooral bij complexere getallen is een rekenmachine handig om nauwkeurige resultaten te krijgen.
• Rond af: In de meeste gevallen is het prima om de omtrek af te ronden op één of twee decimalen.
• Oefen: De beste manier om de formule onder de knie te krijgen, is door te oefenen met verschillende voorbeelden.

Wanneer gebruik je welke formule?

Zoals we eerder hebben gezien, zijn er twee formules voor het berekenen van de omtrek van een cirkel: Omtrek = πd en Omtrek = 2πr. De keuze tussen de twee hangt af van welke informatie je al hebt:

• Gebruik Omtrek = πd als je de diameter van de cirkel kent. Dit is de meest directe manier om de omtrek te berekenen als de diameter al gegeven is.
• Gebruik Omtrek = 2πr als je de straal van de cirkel kent. Als je de straal weet, kun je deze formule gebruiken om de omtrek te berekenen. Je kunt de diameter ook berekenen door de straal te verdubbelen (d = 2r) en vervolgens de formule Omtrek = πd gebruiken.

Het is belangrijk om te onthouden dat beide formules hetzelfde resultaat opleveren, zolang je de juiste waarde voor de diameter of de straal gebruikt.

Praktische toepassingen in de echte wereld

Zoals we al aan het begin van dit artikel hebben aangegeven, is het berekenen van de omtrek van een cirkel veel meer dan alleen een wiskundige oefening. Het heeft talloze praktische toepassingen in verschillende vakgebieden en in het dagelijks leven. Laten we eens kijken naar een paar concrete voorbeelden:

• Engineering: Ingenieurs gebruiken de formule voor de omtrek bij het ontwerpen van wielen, tandwielen, en andere roterende onderdelen. De precieze omtrek is cruciaal voor de prestaties en efficiëntie van deze onderdelen. Bijvoorbeeld, bij het ontwerpen van een fietswiel moet de omtrek nauwkeurig worden berekend om te zorgen dat de fiets de juiste afstand aflegt per omwenteling van het wiel.
• Architectuur: Architecten gebruiken de omtrek bij het ontwerpen van koepels, bogen en andere cirkelvormige structuren. De juiste berekening van de omtrek is essentieel voor de stabiliteit en esthetiek van het gebouw.
• Productie: Fabrikanten gebruiken de formule voor de omtrek bij het produceren van cirkelvormige producten, zoals buizen, kabels en ringen. De precieze omtrek is belangrijk voor de passing en functionaliteit van deze producten.
• Textielindustrie: Bij het maken van kleding, bijvoorbeeld bij het ontwerpen van een rok of een hoed, is het belangrijk om de omtrek te kunnen berekenen om ervoor te zorgen dat de kledingstukken de juiste maat hebben.
• Tuinieren: Bij het aanleggen van een cirkelvormige vijver of bloembed is het handig om de omtrek te berekenen om te bepalen hoeveel materiaal je nodig hebt voor de rand.

Conclusie: Een waardevolle vaardigheid

Het berekenen van de omtrek van een cirkel is een fundamentele vaardigheid die je in veel situaties van pas kan komen. Met de eenvoudige formule en de stapsgewijze uitleg in dit artikel ben je nu in staat om de omtrek van elke cirkel te berekenen, of je nu de diameter of de straal kent. Onthoud de formule (Omtrek = πd of Omtrek = 2πr), oefen met verschillende voorbeelden, en je zult zien dat het berekenen van de omtrek van een cirkel een fluitje van een cent is. Dus, ga erop uit en gebruik deze nieuwe kennis om de wereld om je heen beter te begrijpen en problemen op te lossen!