Hoe Bereken Je De Omtrek Van Een Driehoek

Heb je je ooit afgevraagd hoe je de afstand rondom een driehoek kunt meten? Of misschien ben je een student die worstelt met meetkunde en op zoek is naar een duidelijke uitleg? Deze handleiding is er voor jou! We gaan dieper in op de omtrek van een driehoek, hoe je deze berekent en waarom dit belangrijk is. We houden het simpel en overzichtelijk, zodat iedereen het kan begrijpen.

Wat is de Omtrek van een Driehoek?

De omtrek van eender welke vorm, inclusief een driehoek, is simpelweg de totale lengte van alle zijden samen. Stel je voor dat je een hek rondom een driehoekig stuk land wilt plaatsen; de benodigde lengte van het hek is de omtrek van dat land.

Waarom is dit belangrijk?

Het berekenen van de omtrek van een driehoek is nuttiger dan je misschien denkt. Het kan van pas komen in verschillende situaties:

Architectuur en Bouw: Het berekenen van materiaalbehoefte voor dakconstructies, gevelbekleding of funderingen.
Tuinieren en Landschapsarchitectuur: Het bepalen van de hoeveelheid hekwerk die nodig is voor een driehoekig perk, of de lengte van een rand rondom een driehoekige vijver.
Wiskunde en Meetkunde: Een fundamenteel concept dat de basis vormt voor complexere geometrische berekeningen.
Dagelijks leven: Zelfs bij het inlijsten van een driehoekige foto, of het maken van een driehoekige vlag.

Hoe Bereken je de Omtrek? De Basisformule

De meest eenvoudige manier om de omtrek van een driehoek te berekenen, is door de lengte van alle drie de zijden bij elkaar op te tellen. Dit geldt voor alle soorten driehoeken, of ze nu gelijkzijdig, gelijkbenig of ongelijkzijdig zijn.

De formule is als volgt:

Omtrek (O) = Zijde A + Zijde B + Zijde C

Laten we dit illustreren met een voorbeeld:

Stel, je hebt een driehoek met de volgende zijden:

Zijde A = 5 cm
Zijde B = 7 cm
Zijde C = 9 cm

Om de omtrek te berekenen, tel je deze lengtes bij elkaar op:

O = 5 cm + 7 cm + 9 cm = 21 cm

De omtrek van deze driehoek is dus 21 cm.

Wat als je niet alle zijden weet?

Soms krijg je niet alle drie de zijden van de driehoek direct. Gelukkig zijn er manieren om de ontbrekende zijden te berekenen, afhankelijk van de informatie die je wel hebt.

De Stelling van Pythagoras: Voor Rechthoekige Driehoeken

De stelling van Pythagoras is een krachtig hulpmiddel voor het berekenen van de lengte van een zijde in een rechthoekige driehoek. Een rechthoekige driehoek is een driehoek met een hoek van precies 90 graden (een rechte hoek).

De stelling van Pythagoras stelt:

a² + b² = c²

Waarbij:

a en b de lengtes zijn van de twee korte zijden (de rechthoekszijden).
c de lengte is van de langste zijde, de hypotenusa (de zijde tegenover de rechte hoek).

Voorbeeld:

Stel, je hebt een rechthoekige driehoek waarbij:

Zijde a = 3 cm
Zijde b = 4 cm

Je wilt de lengte van de hypotenusa (zijde c) berekenen.

Volgens de stelling van Pythagoras:

3² + 4² = c²

9 + 16 = c²

25 = c²

Om c te vinden, neem je de wortel van 25:

c = √25 = 5 cm

De hypotenusa is dus 5 cm. Nu je alle drie de zijden kent, kun je de omtrek berekenen zoals eerder uitgelegd.

Goniometrie: Sinus, Cosinus en Tangens

Als je een hoek en de lengte van één zijde van een rechthoekige driehoek kent, kun je goniometrie gebruiken om de lengtes van de andere zijden te berekenen. Goniometrie maakt gebruik van de relaties tussen hoeken en zijden in rechthoekige driehoeken, met behulp van functies zoals sinus (sin), cosinus (cos) en tangens (tan).

De basisdefinities zijn:

Sinus (sin) = Overstaande zijde / Hypotenusa
Cosinus (cos) = Aanliggende zijde / Hypotenusa
Tangens (tan) = Overstaande zijde / Aanliggende zijde

Voorbeeld:

Stel, je hebt een rechthoekige driehoek waarbij:

Hoek α = 30 graden
Hypotenusa (c) = 10 cm

Je wilt de lengte van de overstaande zijde (a) berekenen.

Gebruik de sinus-functie:

sin(30°) = a / 10

We weten dat sin(30°) = 0.5

Dus, 0.5 = a / 10

a = 0.5 * 10 = 5 cm

De overstaande zijde is dus 5 cm. Nu kun je de aanliggende zijde (b) berekenen met behulp van de stelling van Pythagoras of de cosinus-functie. Daarna kun je de omtrek berekenen.

Speciale Driehoeken: Vereenvoudigingen

Sommige driehoeken hebben speciale eigenschappen die het berekenen van hun omtrek vereenvoudigen:

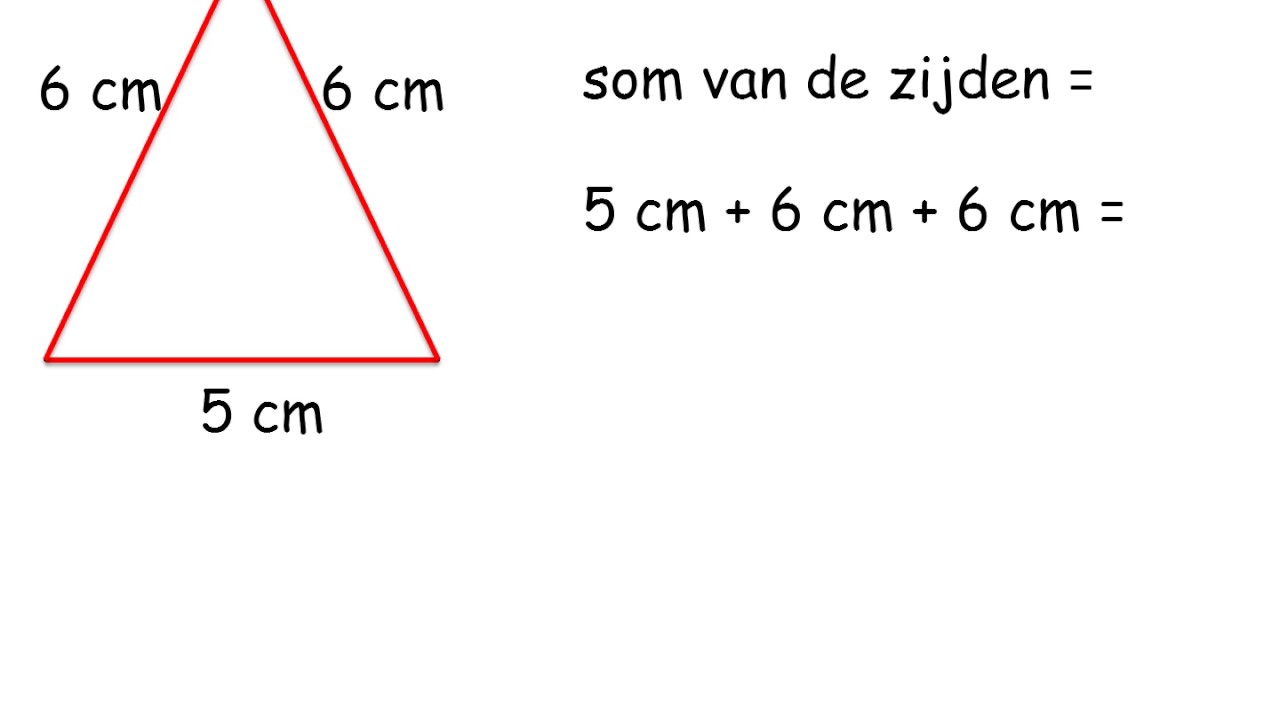
Gelijkzijdige Driehoek: Alle drie de zijden zijn gelijk. De omtrek is simpelweg 3 * (lengte van één zijde).
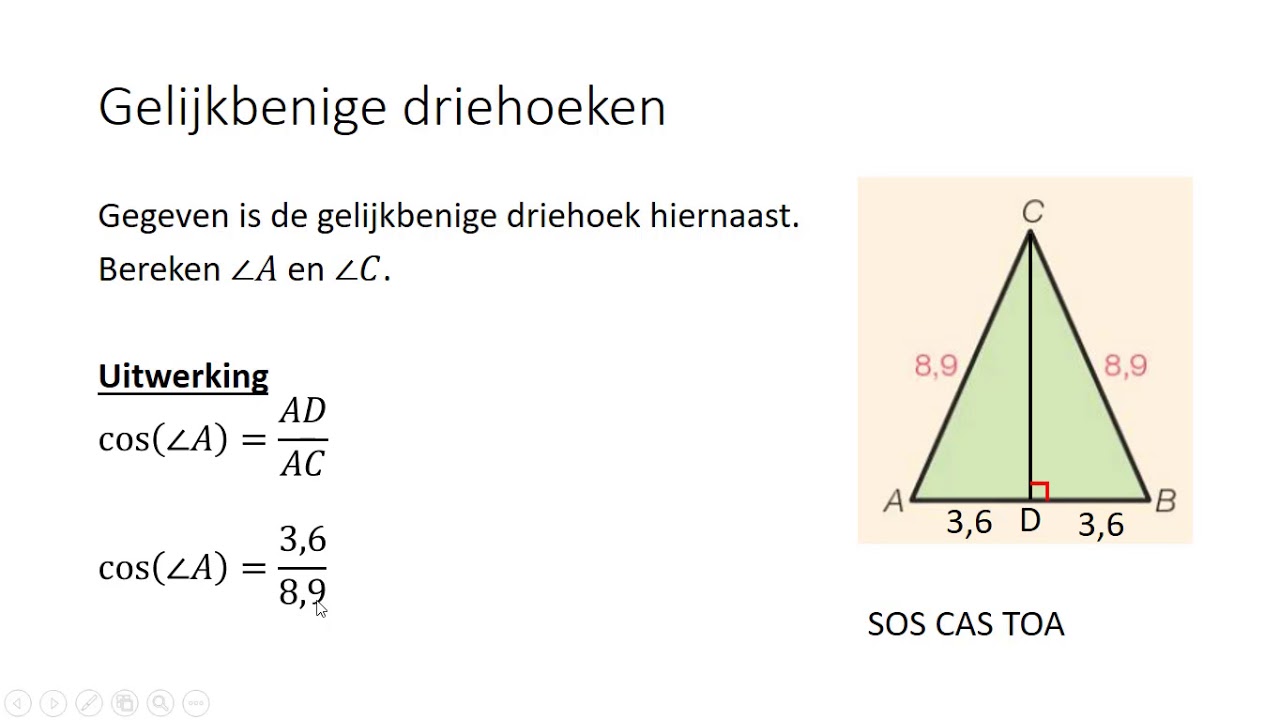
Gelijkbenige Driehoek: Twee zijden zijn gelijk. Je hoeft alleen de lengte van de ongelijke zijde en één van de gelijke zijden te kennen om de omtrek te berekenen.

Tips en Trucs

Let op de eenheden: Zorg ervoor dat alle zijden in dezelfde eenheden staan (bijvoorbeeld, allemaal in centimeters of meters) voordat je ze bij elkaar optelt.
Gebruik een rekenmachine: Voor ingewikkelde berekeningen, vooral met goniometrie, is een rekenmachine een must.
Controleer je antwoord: Is de omtrek logisch gezien de lengtes van de zijden? Een veel te grote of kleine omtrek kan wijzen op een fout.

Conclusie

Het berekenen van de omtrek van een driehoek is een essentiële vaardigheid in de wiskunde en daarbuiten. Of je nu een student bent, een doe-het-zelver of een professional in de bouwsector, het begrijpen van deze principes kan je helpen bij het oplossen van praktische problemen en het nemen van weloverwogen beslissingen. Door de basisformule te kennen, de stelling van Pythagoras te begrijpen, en goniometrie toe te passen, kun je de omtrek van elke driehoek berekenen, ongeacht de complexiteit. Oefening baart kunst, dus blijf oefenen en je zult merken dat het steeds gemakkelijker wordt! Succes!