Hoe Bereken Je De Opp Van Een Driehoek

Herken je dat? Je zit met een geometrisch probleem, een bouwproject, of misschien ben je gewoon nieuwsgierig en wil je weten hoe je de oppervlakte van een driehoek berekent. Het kan soms intimiderend lijken, vooral als wiskunde niet je sterkste punt is. Maar maak je geen zorgen! Het is eigenlijk verrassend eenvoudig als je eenmaal de basisprincipes begrijpt. We gaan samen stap voor stap ontdekken hoe je dit kunt aanpakken, zonder moeilijke formules of ingewikkeld jargon.

De Basis: De Oppervlakteformule

De meest fundamentele formule voor het berekenen van de oppervlakte van een driehoek is:

Oppervlakte = ½ * basis * hoogte

Dit klinkt misschien simpel, en dat is het in principe ook! Laten we eens kijken wat ‘basis’ en ‘hoogte’ precies betekenen.

Wat zijn de Basis en Hoogte?

De basis van een driehoek is eigenlijk gewoon één van de zijden van de driehoek. Je kunt elke zijde kiezen als de basis.

De hoogte is de loodrechte afstand van de basis tot de tegenoverliggende hoek. Denk aan een rechte lijn die van de top van de driehoek loodrecht naar de basis loopt. Het is belangrijk dat deze lijn een hoek van 90 graden maakt met de basis. Als je deze twee waarden hebt, ben je klaar om de oppervlakte te berekenen!

Voorbeeld: Stel je voor dat de basis van een driehoek 8 cm is en de hoogte 5 cm. Dan is de oppervlakte:

Oppervlakte = ½ * 8 cm * 5 cm = 20 cm²

Dus de oppervlakte van deze driehoek is 20 vierkante centimeter.

Verschillende Soorten Driehoeken, Verschillende Benaderingen

Er zijn verschillende soorten driehoeken, en hoewel de basisformule altijd hetzelfde blijft, kan de manier waarop je de hoogte vindt variëren.

Rechthoekige Driehoeken

Bij een rechthoekige driehoek is het heel eenvoudig. Een van de zijden die de rechte hoek vormen, kan als basis worden genomen, en de andere zijde is dan de hoogte. De rechte hoek maakt het makkelijk, je hoeft geen extra berekeningen te doen om de hoogte te vinden!

Gelijkzijdige Driehoeken

Een gelijkzijdige driehoek heeft drie gelijke zijden en drie gelijke hoeken (van 60 graden). Om de hoogte van een gelijkzijdige driehoek te vinden, kun je de stelling van Pythagoras gebruiken. Als de zijde bijvoorbeeld ‘a’ is, dan is de hoogte (h) gelijk aan (a√3)/2.

Stel, de zijde van een gelijkzijdige driehoek is 6 cm. Dan is de hoogte:

h = (6 * √3) / 2 ≈ 5.2 cm

Vervolgens bereken je de oppervlakte zoals eerder beschreven: ½ * 6 cm * 5.2 cm ≈ 15.6 cm²

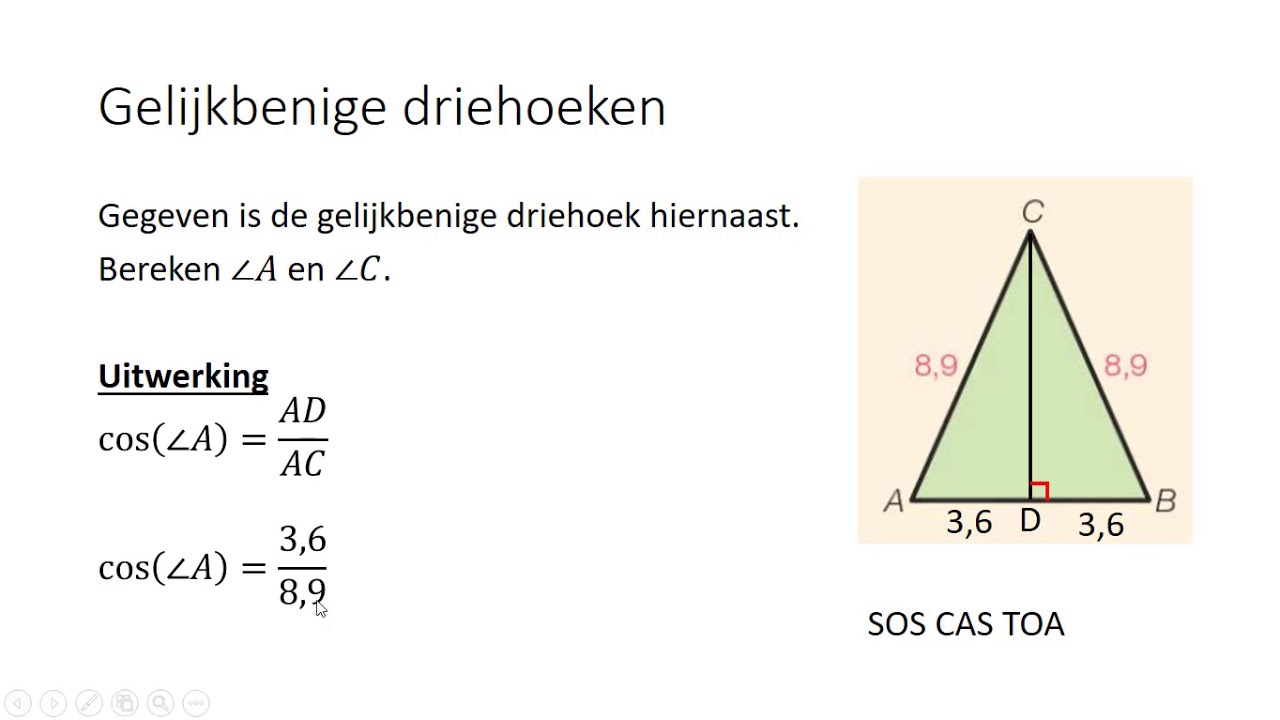
Gelijkbenige Driehoeken

Een gelijkbenige driehoek heeft twee gelijke zijden. Om de hoogte te vinden, trek je een lijn van de hoek tussen de twee gelijke zijden loodrecht naar de basis. Deze lijn deelt de basis in twee gelijke delen. Ook hier kun je, afhankelijk van de gegeven informatie, de stelling van Pythagoras gebruiken om de hoogte te berekenen.

Ongelijkzijdige Driehoeken (Scalene Triangles)

Ongelijkzijdige driehoeken hebben drie verschillende zijden en drie verschillende hoeken. Hier wordt het iets lastiger om de hoogte te vinden. Je kunt hiervoor trigonometrie gebruiken (sinus, cosinus, tangens) als je de hoeken kent, of je kunt de formule van Heron gebruiken als je de lengte van alle drie de zijden kent.

De Formule van Heron: Wanneer Je Alleen de Zijden Kent

De formule van Heron is een krachtig hulpmiddel als je de lengtes van alle drie de zijden (a, b, en c) van een driehoek kent, maar niet de hoogte. De formule is:

Oppervlakte = √(s(s-a)(s-b)(s-c))

Waarbij 's' de halve omtrek van de driehoek is, oftewel:

s = (a + b + c) / 2

Voorbeeld: Stel, de zijden van een driehoek zijn 5 cm, 7 cm en 8 cm.

Eerst berekenen we de halve omtrek (s):

s = (5 + 7 + 8) / 2 = 10 cm

Vervolgens vullen we de formule van Heron in:

Oppervlakte = √(10(10-5)(10-7)(10-8)) = √(10 * 5 * 3 * 2) = √300 ≈ 17.32 cm²

Dus de oppervlakte van deze driehoek is ongeveer 17.32 vierkante centimeter.

Trigonometrie: De Kracht van Hoeken

Als je een zijde en een hoek kent, kun je trigonometrie gebruiken om de hoogte te berekenen. Stel dat je zijde 'b' kent en de hoek 'A' tegenover de hoogte. Dan geldt:

Hoogte (h) = b * sin(A)

Vervolgens kun je de basisformule (½ * basis * hoogte) gebruiken om de oppervlakte te berekenen. Dit is vooral handig bij ongelijkzijdige driehoeken waar de hoogte niet direct gegeven is.

Praktische Toepassingen

Waarom is dit allemaal belangrijk? De berekening van de oppervlakte van een driehoek is niet alleen een theoretische oefening. Het heeft talloze praktische toepassingen:

• Bouwkunde en Architectuur: Het berekenen van de oppervlakte van dakspanten, gevels, en andere driehoekige structuren.
• Landmeetkunde: Het bepalen van de oppervlakte van landpercelen.
• Engineering: Het ontwerpen van bruggen, machines en andere constructies.
• Grafisch Ontwerp en Spelontwikkeling: Het berekenen van de oppervlakte van polygonen, die vaak uit driehoeken bestaan.
• Alledaagse Klussen: Het bepalen van de hoeveelheid verf die nodig is voor een driehoekige muur, of de hoeveelheid stof voor een driehoekig zeil.

Kortom, de kennis van hoe je de oppervlakte van een driehoek berekent, is een waardevolle vaardigheid in veel verschillende domeinen.

Tips & Tricks voor Succes

• Zorg dat je de juiste eenheden gebruikt: Als de basis in centimeters is, moet de hoogte ook in centimeters zijn. De oppervlakte wordt dan in vierkante centimeters (cm²) uitgedrukt.
• Teken een schets: Het kan helpen om de driehoek te tekenen en de bekende waarden aan te geven. Dit maakt het makkelijker om de basis en de hoogte te identificeren.
• Wees nauwkeurig: Bij complexe berekeningen, zoals de formule van Heron, is het belangrijk om nauwkeurig te zijn met de cijfers om fouten te voorkomen.
• Controleer je antwoord: Ziet je antwoord er logisch uit? Een extreem grote of kleine oppervlakte kan een teken zijn van een fout in de berekening.

Conclusie

Het berekenen van de oppervlakte van een driehoek is, ondanks dat het in eerste instantie misschien ingewikkeld lijkt, een relatief eenvoudige taak, mits je de juiste formules en methoden kent. Van de basisformule (½ * basis * hoogte) tot de formule van Heron en trigonometrie, er zijn verschillende manieren om dit probleem aan te pakken, afhankelijk van de beschikbare informatie.

Hopelijk heeft dit artikel je een helder en praktisch overzicht gegeven van hoe je de oppervlakte van een driehoek kunt berekenen. Nu ben je klaar om je nieuwe kennis in de praktijk te brengen en geometrische uitdagingen met vertrouwen aan te gaan! Blijf oefenen en experimenteren, en je zult merken dat het steeds makkelijker wordt. En onthoud: wiskunde is geen obstakel, maar een hulpmiddel!