Hoe Bereken Je De Oppervlakte Van Een Driehoek

Heb je je ooit afgevraagd hoe je de oppervlakte van een driehoek berekent? Misschien worstel je met wiskunde op school, of misschien ben je een klusser die de hoeveelheid verf moet inschatten voor een gevel met driehoekige elementen. Wat de reden ook is, het berekenen van de oppervlakte van een driehoek kan soms ingewikkeld lijken. Maar maak je geen zorgen, het is eenvoudiger dan je denkt! We duiken erin en ontdekken verschillende manieren om dit te doen.

Waarom is het belangrijk om de oppervlakte van een driehoek te kunnen berekenen?

Het is meer dan alleen een wiskundige oefening. Denk eens aan de volgende scenario's:

Architectuur en constructie: Het berekenen van de benodigde materialen voor dakconstructies, gevels of zelfs decoratieve elementen.
Landmeten: Het bepalen van de oppervlakte van landpercelen met onregelmatige vormen.
Gaming en grafisch ontwerp: Het renderen van objecten en scènes.
Klusprojecten: Het inschatten van de benodigde hoeveelheid verf, behang of tegels.

Het beheersen van deze vaardigheid geeft je dus direct toepasbare kennis voor diverse praktische situaties. Het is niet alleen theorie, maar concrete bruikbaarheid.

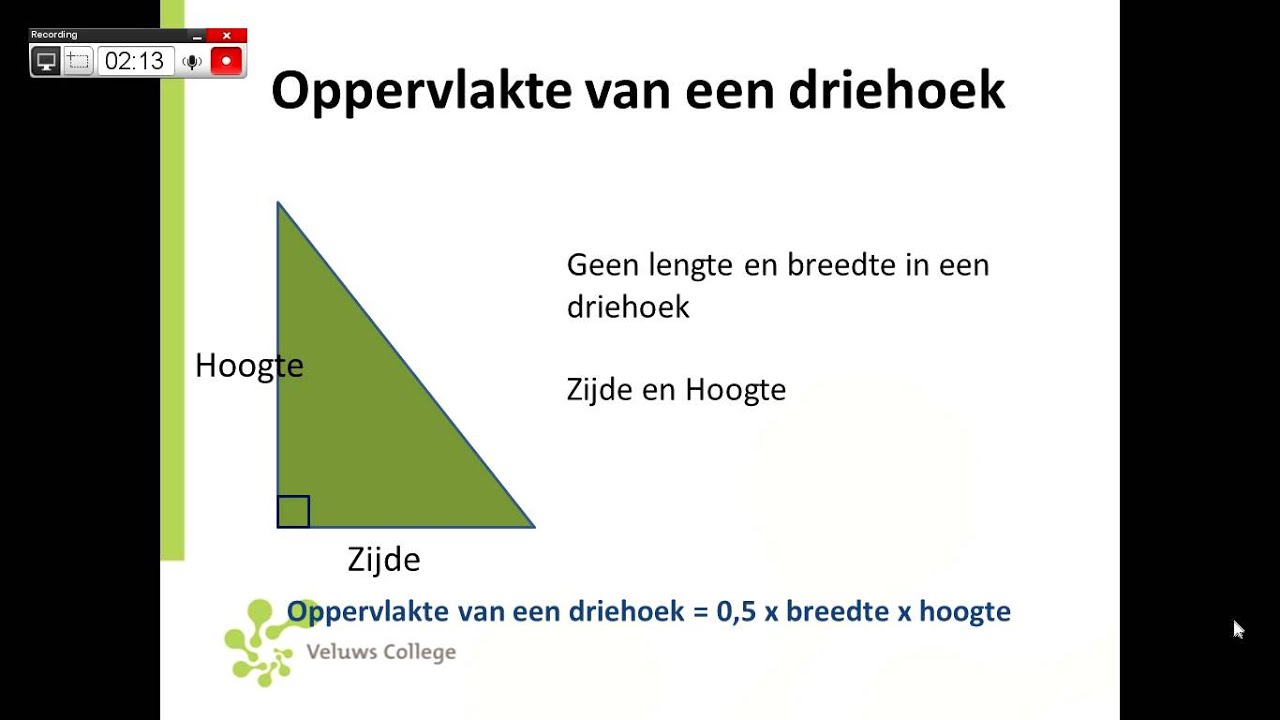
De basisformule: Basis x Hoogte / 2

Dit is de meest bekende en meest gebruikte formule voor het berekenen van de oppervlakte van een driehoek:

Oppervlakte = (Basis x Hoogte) / 2

Maar wat betekenen 'basis' en 'hoogte' precies?

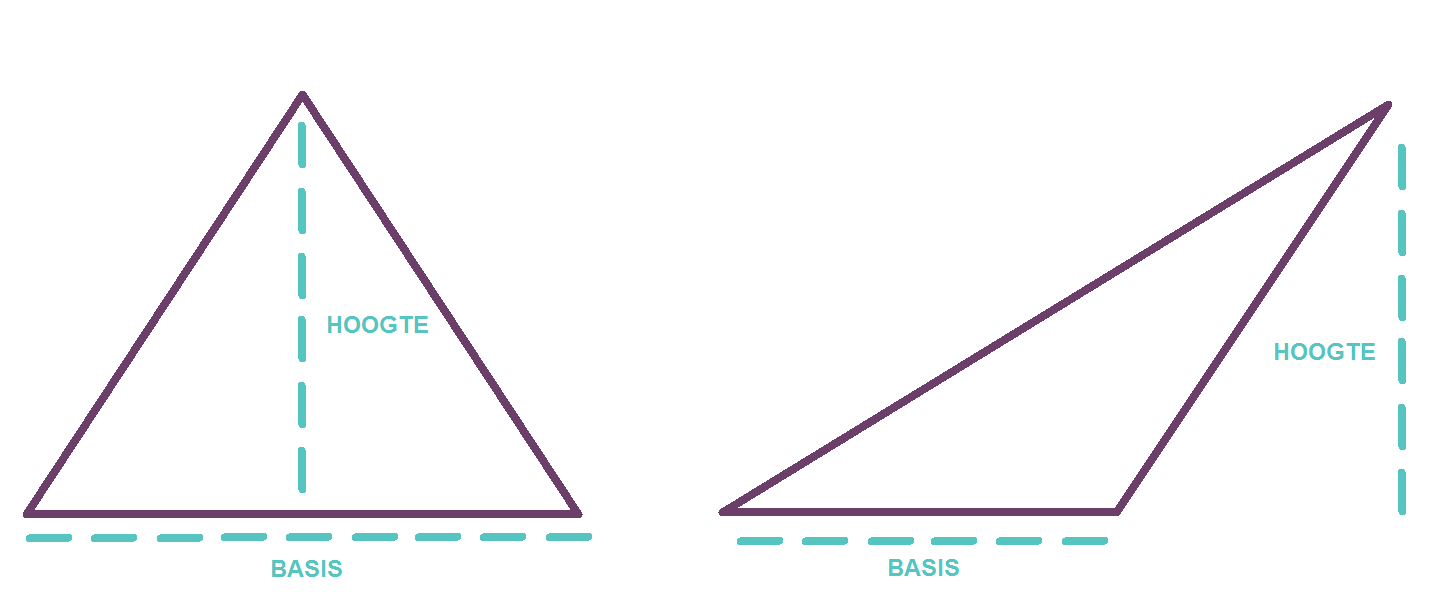
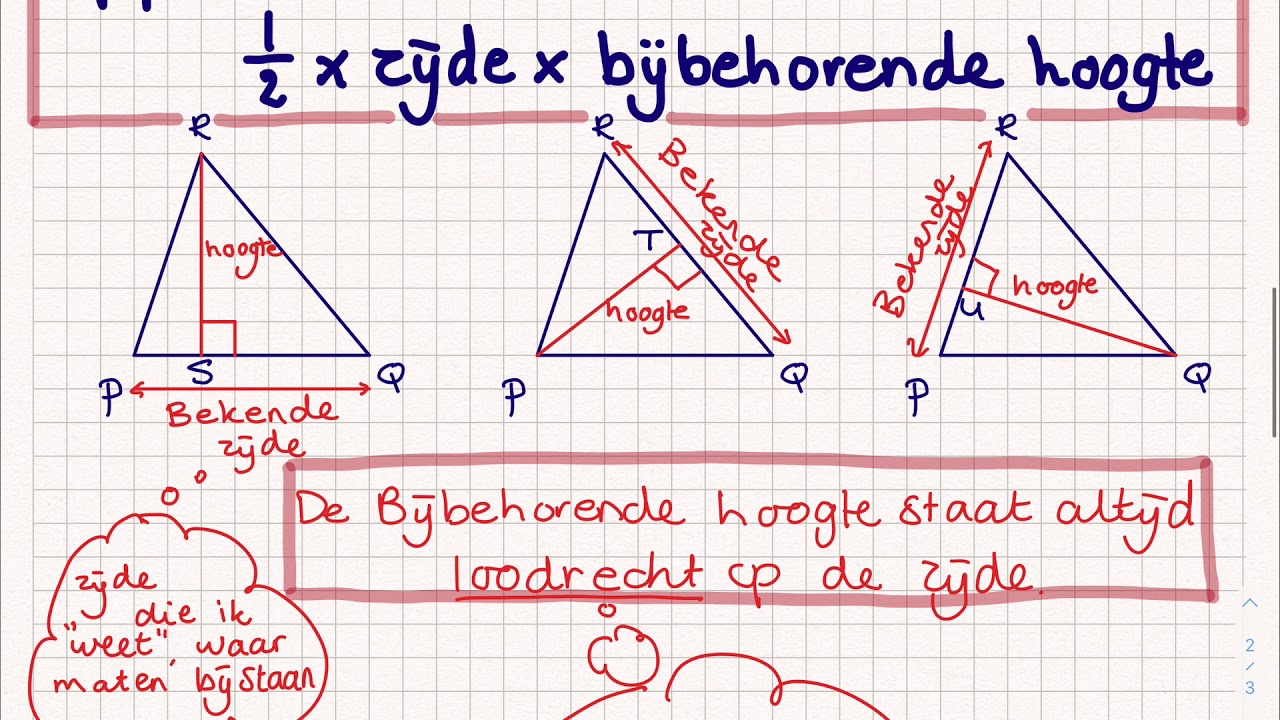
De basis (b): Dit is een van de zijden van de driehoek. Je kunt elke zijde als basis kiezen.
De hoogte (h): Dit is de loodrechte afstand van de basis tot de tegenoverliggende hoekpunt. Let op: de hoogte is niet per se een van de zijden van de driehoek!

Voorbeeld: Stel, je hebt een driehoek met een basis van 8 cm en een hoogte van 5 cm. De oppervlakte bereken je als volgt:

Oppervlakte = (8 cm x 5 cm) / 2 = 20 cm²

Dus de oppervlakte van deze driehoek is 20 vierkante centimeter.

Wat als je de hoogte niet weet?

Soms is de hoogte niet direct gegeven. In dat geval kun je andere methoden gebruiken, die we later bespreken.

De formule van Heron: Voor driehoeken waar je alleen de zijden kent

Wat als je de lengte van alle drie de zijden van een driehoek kent, maar niet de hoogte? Dan komt de formule van Heron van pas. Deze formule lijkt wat ingewikkelder, maar is zeer krachtig.

De formule van Heron luidt:

Oppervlakte = √(s(s-a)(s-b)(s-c))

Waar:

a, b en c de lengtes van de drie zijden van de driehoek zijn.
s de halve omtrek van de driehoek is, berekend als: s = (a + b + c) / 2

Voorbeeld: Stel, je hebt een driehoek met zijden van 5 cm, 7 cm en 8 cm. Eerst bereken je de halve omtrek:

s = (5 cm + 7 cm + 8 cm) / 2 = 10 cm

Vervolgens vul je de formule van Heron in:

Oppervlakte = √(10(10-5)(10-7)(10-8)) = √(10 x 5 x 3 x 2) = √300 ≈ 17.32 cm²

Dus de oppervlakte van deze driehoek is ongeveer 17.32 vierkante centimeter.

Waarom werkt de formule van Heron?

De formule van Heron is gebaseerd op trigonometrische principes en is een afgeleide van andere formules. Het voordeel is dat je geen hoeken hoeft te kennen om de oppervlakte te berekenen.

Oppervlakte berekenen met trigonometrie: Als je een hoek en twee zijden kent

Als je de lengte van twee zijden van een driehoek kent, én de hoek die deze zijden insluiten, kun je de oppervlakte berekenen met behulp van trigonometrie. Deze methode is vooral handig bij niet-rechthoekige driehoeken.

De formule is:

Oppervlakte = ½ * a * b * sin(C)

Waar:

a en b de lengtes van de twee bekende zijden zijn.
C de hoek is die ingesloten wordt door de zijden a en b.
sin(C) de sinus van hoek C is. Je hebt hiervoor een rekenmachine nodig die sinus kan berekenen.

Voorbeeld: Stel, je hebt een driehoek met zijden van 6 cm en 9 cm, en de ingesloten hoek is 30 graden. Dan bereken je de oppervlakte als volgt:

Oppervlakte = ½ * 6 cm * 9 cm * sin(30°) = ½ * 6 cm * 9 cm * 0.5 = 13.5 cm²

Dus de oppervlakte van deze driehoek is 13.5 vierkante centimeter.

Waarom trigonometrie gebruiken?

Trigonometrie biedt een krachtige manier om de oppervlakte van driehoeken te berekenen, zelfs als je niet de hoogte direct kunt meten. Het is essentieel in situaties waar hoeken en zijdelengtes bekender zijn dan de hoogte.

Speciale gevallen: Rechthoekige Driehoeken

Rechthoekige driehoeken zijn extra gemakkelijk! Een rechthoekige driehoek heeft een hoek van 90 graden. De twee zijden die de rechte hoek vormen, zijn de basis en de hoogte!

Dus, als je een rechthoekige driehoek hebt, kun je gewoon de lengtes van de twee korte zijden (de rechthoekszijden) vermenigvuldigen en delen door 2:

Oppervlakte = (Rechthoekszijde 1 x Rechthoekszijde 2) / 2

Voorbeeld: Een rechthoekige driehoek heeft rechthoekszijden van 3 cm en 4 cm. De oppervlakte is:

Oppervlakte = (3 cm x 4 cm) / 2 = 6 cm²

Dit maakt het berekenen van de oppervlakte van een rechthoekige driehoek bijzonder eenvoudig.

Veelgemaakte fouten en hoe ze te vermijden

Er zijn een paar valkuilen waar veel mensen in trappen bij het berekenen van de oppervlakte van een driehoek:

De hoogte verwarren met een zijde: De hoogte moet loodrecht op de basis staan. Niet elke zijde is de hoogte!
Verkeerde eenheden: Zorg ervoor dat je alle metingen in dezelfde eenheden hebt (bijvoorbeeld allemaal in centimeters of allemaal in meters). De oppervlakte zal dan in vierkante centimeters (cm²) of vierkante meters (m²) zijn.
Verkeerde formule kiezen: Gebruik de juiste formule voor de gegeven informatie. Als je alleen de zijden kent, gebruik dan Heron. Als je een basis en hoogte hebt, gebruik dan de basis x hoogte / 2 formule.
Rekenfouten: Controleer je berekeningen zorgvuldig!

Door je bewust te zijn van deze veelgemaakte fouten, kun je ze gemakkelijk vermijden en nauwkeurigere resultaten behalen.

Samenvatting en tips

Laten we de belangrijkste punten nog eens samenvatten:

Basis x Hoogte / 2: De meest gebruikelijke formule, vereist de basis en de hoogte.
Formule van Heron: Gebruik als je alleen de lengtes van de drie zijden kent.
Trigonometrie (½ * a * b * sin(C)): Gebruik als je twee zijden en de ingesloten hoek kent.
Rechthoekige driehoek: Gebruik de rechthoekszijden als basis en hoogte.

Tips:

Maak een schets van de driehoek. Dit helpt je om de basis en hoogte (of andere relevante informatie) beter te visualiseren.
Controleer altijd of je de juiste formule gebruikt.
Let op de eenheden en zorg ervoor dat ze consistent zijn.
Oefening baart kunst! Hoe meer je oefent, hoe gemakkelijker het wordt.

Alternatieve benaderingen en tools

Er zijn ook handige online calculators beschikbaar die de oppervlakte van een driehoek voor je kunnen berekenen. Deze tools zijn vooral handig als je snel een resultaat nodig hebt of als je ingewikkelde berekeningen wilt vermijden. Zoek simpelweg naar "driehoek oppervlakte calculator" op Google of een andere zoekmachine.

Daarnaast zijn er geavanceerdere softwarepakketten, zoals CAD-programma's (Computer-Aided Design), die gebruikt worden in de architectuur en engineering. Deze programma's kunnen automatisch de oppervlakte van complexe vormen, waaronder driehoeken, berekenen.

Conclusie

Het berekenen van de oppervlakte van een driehoek is een essentiële vaardigheid met toepassingen in diverse vakgebieden en alledaagse situaties. Door de verschillende formules en methoden te begrijpen, kun je elk probleem met betrekking tot de oppervlakte van een driehoek aanpakken. Hopelijk heeft dit artikel je geholpen om het proces te demystificeren en je zelfvertrouwen te vergroten.

Dus, waar ga jij deze kennis voor gebruiken? Ga je een bouwproject plannen, een landperceel meten, of gewoon je wiskundige vaardigheden aanscherpen?