Hoe Bereken Je De Standaardafwijking

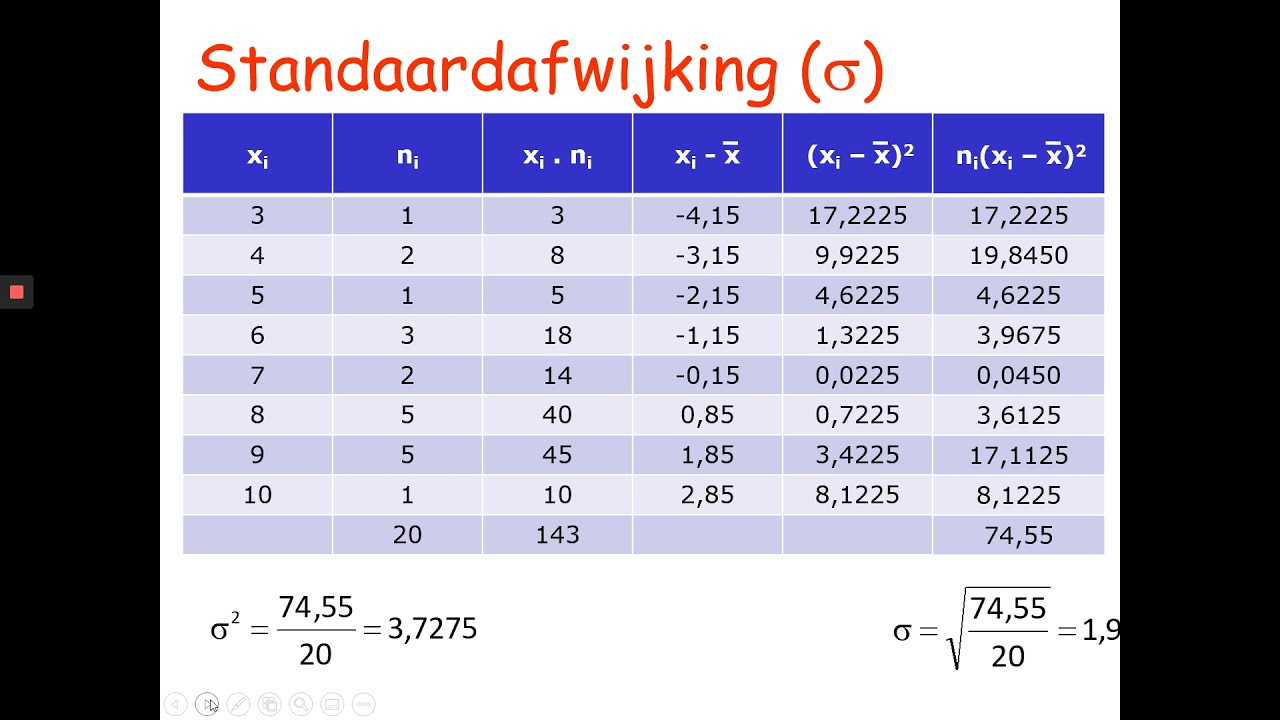
Heb je je ooit afgevraagd hoe je de spreiding van een dataset kunt meten? Of misschien worstel je met statistiek huiswerk en ben je hopeloos op zoek naar een eenvoudige uitleg van de standaardafwijking? Zo ja, dan ben je hier aan het juiste adres. Statistiek kan intimiderend lijken, maar met de juiste begeleiding kan het verrassend eenvoudig zijn. Laten we samen de mysteriën van de standaardafwijking ontrafelen!

Wat is de Standaardafwijking?

De standaardafwijking is een cruciale maatstaf in de statistiek. Het geeft aan hoe verspreid de data in een dataset zijn ten opzichte van het gemiddelde. Simpel gezegd: een lage standaardafwijking betekent dat de meeste getallen dicht bij het gemiddelde liggen. Een hoge standaardafwijking betekent dat de getallen meer verspreid zijn. Denk aan een groep leerlingen die een toets maken. Een lage standaardafwijking betekent dat de meeste leerlingen ongeveer hetzelfde scoorden. Een hoge standaardafwijking betekent dat er grote verschillen in de scores waren.

Denk aan het gooien van darts. Als je heel consistent bent en al je darts dicht bij de bullseye terechtkomen, heb je een lage standaardafwijking. Als je darts overal op het bord belanden, heb je een hoge standaardafwijking.

Waarom is de Standaardafwijking Belangrijk?

De standaardafwijking is meer dan alleen een getal; het is een krachtig instrument dat in diverse velden wordt gebruikt:

Financiën: Het helpt beleggers het risico van een investering te beoordelen. Een hogere standaardafwijking duidt op een hoger risico.
Wetenschap: Onderzoekers gebruiken het om de betrouwbaarheid van hun experimenten te evalueren.
Onderwijs: Leraren gebruiken het om de spreiding van de prestaties van hun leerlingen te begrijpen.
Kwaliteitscontrole: Bedrijven gebruiken het om de consistentie van hun producten te bewaken.

In feite, overal waar data wordt geanalyseerd, komt de standaardafwijking van pas. Het geeft context en helpt ons patronen en afwijkingen te identificeren.

Hoe Bereken je de Standaardafwijking: Een Stap-voor-Stap Handleiding

Laten we nu de stappen doorlopen om de standaardafwijking te berekenen. Maak je geen zorgen, we maken het zo eenvoudig mogelijk!

Stap 1: Bereken het Gemiddelde (Mean)

Het gemiddelde is de som van alle getallen in je dataset, gedeeld door het aantal getallen. Dit is een bekende basisberekening.

Formule: Gemiddelde = (Som van alle waarden) / (Aantal waarden)

Voorbeeld: Stel dat je de volgende dataset hebt: 2, 4, 6, 8, 10. Het gemiddelde is (2 + 4 + 6 + 8 + 10) / 5 = 30 / 5 = 6.

Stap 2: Bereken de Afwijking van Elke Waarde van het Gemiddelde

Voor elk getal in je dataset trek je het gemiddelde af. Dit geeft je de afwijking van die waarde ten opzichte van het gemiddelde.

Formule: Afwijking = Waarde - Gemiddelde

Voorbeeld (gebruikmakend van de vorige dataset):

2 - 6 = -4
4 - 6 = -2
6 - 6 = 0
8 - 6 = 2
10 - 6 = 4

Stap 3: Kwadrateer Elke Afwijking

Vervolgens kwadrateren we elke afwijking die we in de vorige stap hebben berekend. Dit is belangrijk omdat het negatieve waarden elimineert en de bijdrage van grotere afwijkingen benadrukt.

Formule: Gekwadrateerde Afwijking = (Afwijking)²

Voorbeeld:

(-4)² = 16
(-2)² = 4
(0)² = 0
(2)² = 4
(4)² = 16

Stap 4: Bereken de Som van de Gekwadrateerde Afwijkingen

Tel alle gekwadrateerde afwijkingen bij elkaar op. Dit geeft ons een idee van de totale variabiliteit in de dataset.

Formule: Som van Gekwadrateerde Afwijkingen = Σ(Gekwadrateerde Afwijkingen)

Voorbeeld: 16 + 4 + 0 + 4 + 16 = 40

Stap 5: Deel de Som van de Gekwadrateerde Afwijkingen door (n-1)

Hier komt een belangrijk concept om de hoek kijken: n-1. Dit wordt de vrijheidsgraad genoemd. We gebruiken n-1 in plaats van n (het totale aantal waarden) wanneer we een steekproef gebruiken om de standaardafwijking van een grotere populatie te schatten. Dit helpt vertekening te corrigeren.

Formule: Variantie (steekproef) = (Som van Gekwadrateerde Afwijkingen) / (n - 1)

Formule: Variantie (populatie) = (Som van Gekwadrateerde Afwijkingen) / (n)

Voorbeeld (steekproef): 40 / (5 - 1) = 40 / 4 = 10

Voorbeeld (populatie): 40 / (5) = 8

Stap 6: Neem de Vierkantswortel van het Resultaat

Tenslotte, nemen we de vierkantswortel van de variantie. Dit geeft ons de standaardafwijking. De vierkantswortel brengt de waarde terug naar de oorspronkelijke eenheden van de data, waardoor het beter interpreteerbaar is.

Formule: Standaardafwijking = √(Variantie)

Voorbeeld (steekproef): √(10) ≈ 3.16

Voorbeeld (populatie): √(8) ≈ 2.83

Dus, de standaardafwijking van onze dataset (2, 4, 6, 8, 10) is ongeveer 3.16 (voor een steekproef) of 2.83 (voor een populatie). Dit betekent dat de waarden in de dataset gemiddeld ongeveer 3.16 (of 2.83) afwijken van het gemiddelde (6).

Een Praktisch Voorbeeld: De Lengte van Studenten

Laten we een ander voorbeeld bekijken. Stel je voor dat je de lengte van 7 studenten meet (in centimeters): 165, 170, 175, 180, 160, 172, 168.

Gemiddelde: (165 + 170 + 175 + 180 + 160 + 172 + 168) / 7 = 170
Afwijkingen: -5, 0, 5, 10, -10, 2, -2
Gekwadrateerde Afwijkingen: 25, 0, 25, 100, 100, 4, 4
Som van Gekwadrateerde Afwijkingen: 25 + 0 + 25 + 100 + 100 + 4 + 4 = 258
Variantie (steekproef): 258 / (7 - 1) = 258 / 6 = 43
Standaardafwijking (steekproef): √43 ≈ 6.56

De standaardafwijking van de lengte van de studenten is ongeveer 6.56 cm. Dit geeft aan dat de lengtes van de studenten gemiddeld ongeveer 6.56 cm afwijken van de gemiddelde lengte van 170 cm.

Tips en Trucs voor het Berekenen van de Standaardafwijking

Gebruik een Rekenmachine of Spreadsheet: Gelukkig hoef je deze berekeningen niet altijd met de hand te doen. Rekenmachines en spreadsheetprogramma's zoals Excel hebben ingebouwde functies om de standaardafwijking te berekenen. In Excel, kun je de functie "=STDEV.S()" gebruiken voor een steekproef of "=STDEV.P()" voor een populatie.
Wees Aandachtig voor Decimalen: Rond getallen correct af om nauwkeurige resultaten te krijgen.
Begrijp het Verschil Tussen Steekproef en Populatie: Gebruik de juiste formule (n-1 of n) afhankelijk van of je met een steekproef of een hele populatie werkt.
Oefening Baart Kunst: Hoe meer je oefent met het berekenen van de standaardafwijking, hoe comfortabeler je er mee zult worden.

Conclusie

De standaardafwijking is een krachtig hulpmiddel om de spreiding van data te begrijpen en te interpreteren. Hoewel de berekening in eerste instantie ingewikkeld kan lijken, is het met de juiste stappen en hulpmiddelen goed te doen. Hopelijk heeft dit artikel je geholpen om de standaardafwijking beter te begrijpen en je statistische vaardigheden verder te ontwikkelen. Blijf oefenen en experimenteren, en voor je het weet, ben je een expert!

Vergeet niet: statistiek is geen magie, het is een hulpmiddel om de wereld om ons heen beter te begrijpen. En de standaardafwijking is een van de belangrijkste gereedschappen in die toolkit. Succes!