Hoe Bereken Je De Stelling Van Pythagoras
De stelling van Pythagoras is een van de meest fundamentele en bekende stellingen in de wiskunde, en specifiek in de meetkunde. Het biedt een eenvoudige, maar krachtige relatie tussen de zijden van een rechthoekige driehoek. Deze stelling is niet alleen een hoeksteen van de wiskunde, maar heeft ook talloze toepassingen in de praktijk, van architectuur tot navigatie.
Wat is de Stelling van Pythagoras?
De stelling van Pythagoras stelt dat in een rechthoekige driehoek (een driehoek met een hoek van 90 graden), het kwadraat van de lengte van de hypotenusa (de zijde tegenover de rechte hoek) gelijk is aan de som van de kwadraten van de lengtes van de andere twee zijden (de rechthoekszijden). Met andere woorden:
a2 + b2 = c2
Waar:
- a en b de lengtes zijn van de rechthoekszijden.
- c de lengte is van de hypotenusa.
De Onderdelen van een Rechthoekige Driehoek
Het is belangrijk om de verschillende onderdelen van een rechthoekige driehoek te begrijpen:
- Rechte Hoek: De hoek van 90 graden.
- Hypotenusa: De zijde tegenover de rechte hoek. Dit is altijd de langste zijde van de driehoek.
- Rechthoekszijden: De twee zijden die de rechte hoek vormen.
Hoe Bereken je de Stelling van Pythagoras?
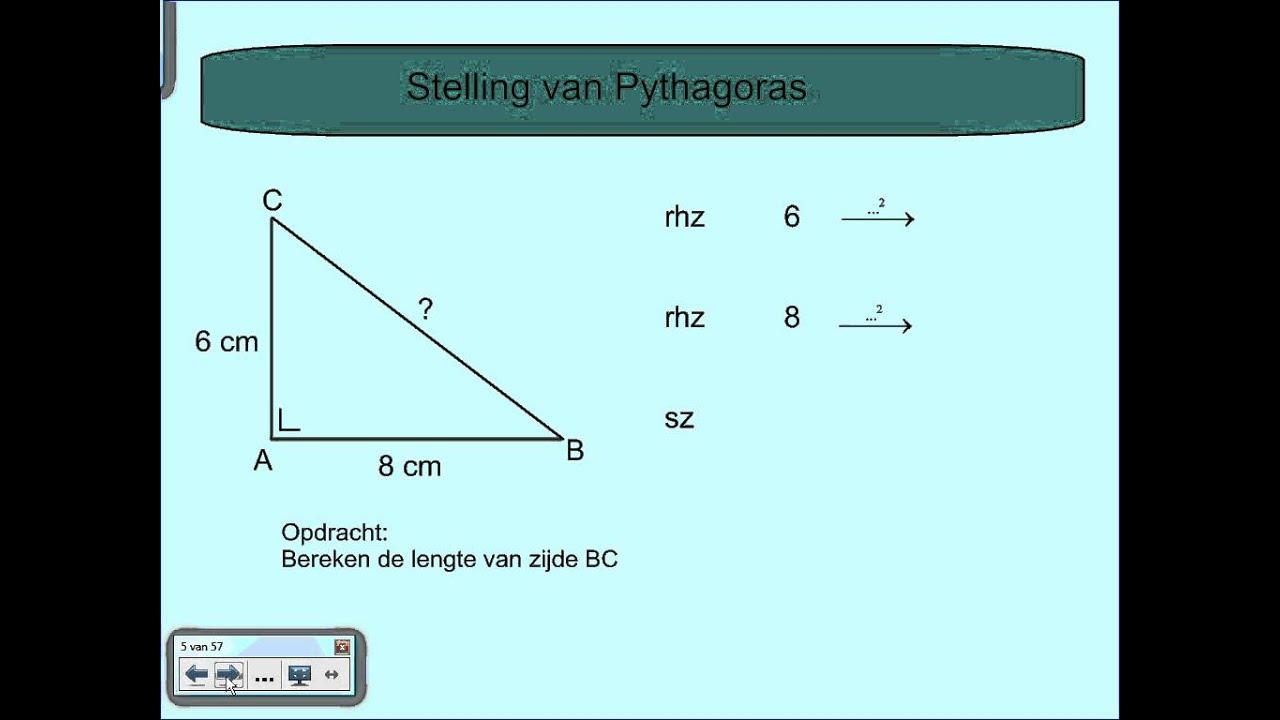
Het berekenen met de stelling van Pythagoras is relatief eenvoudig als je de lengtes van twee zijden van een rechthoekige driehoek kent. Laten we eens kijken naar verschillende scenario's:
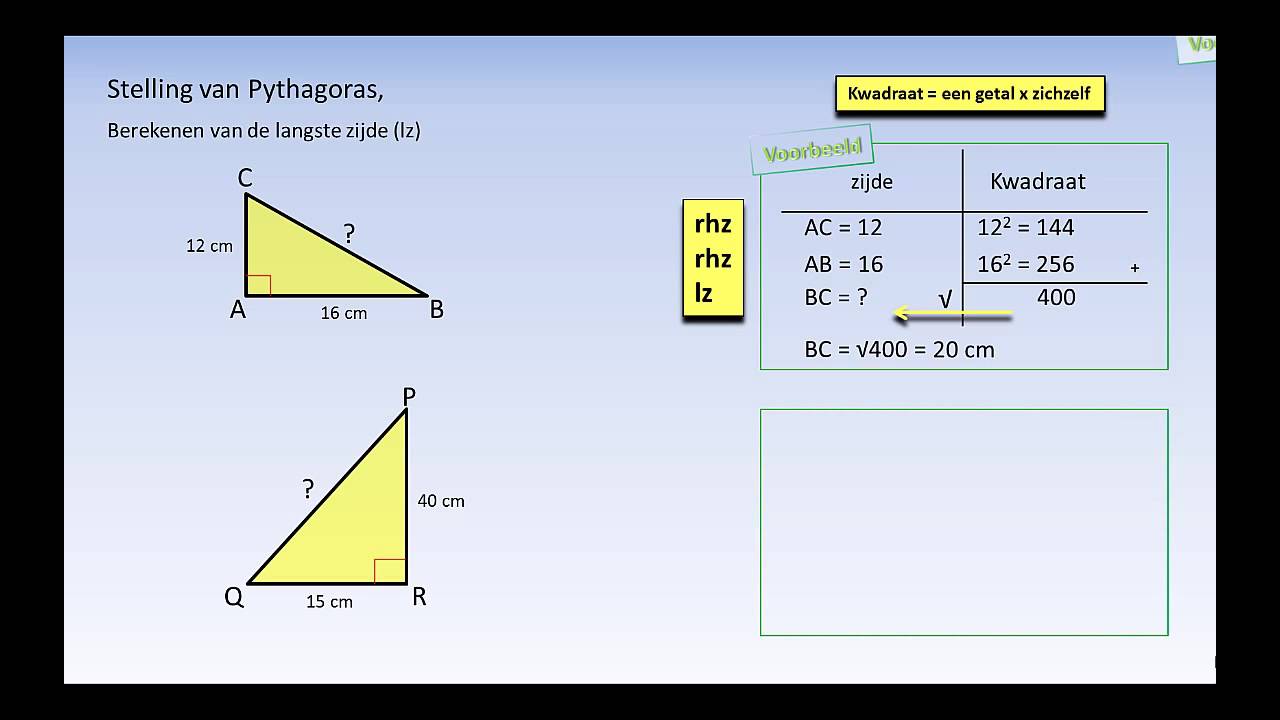
Scenario 1: Bereken de Hypotenusa (c)
Stel dat je de lengtes van de rechthoekszijden a en b kent, en je wilt de lengte van de hypotenusa c berekenen. Je gebruikt de basisformule:
a2 + b2 = c2
Voorbeeld:
Stel dat a = 3 en b = 4.
- Bereken de kwadraten van a en b: 32 = 9 en 42 = 16
- Tel de kwadraten op: 9 + 16 = 25
- Neem de vierkantswortel van de som om c te vinden: √25 = 5
Dus, de lengte van de hypotenusa c is 5.
Scenario 2: Bereken een Rechthoekszijde (a of b)
Stel dat je de lengte van de hypotenusa c en een van de rechthoekszijden (bijvoorbeeld b) kent, en je wilt de andere rechthoekszijde a berekenen. Je kunt de formule herschrijven:
a2 = c2 - b2
Voorbeeld:
Stel dat c = 13 en b = 5.
- Bereken de kwadraten van c en b: 132 = 169 en 52 = 25
- Trek het kwadraat van b af van het kwadraat van c: 169 - 25 = 144
- Neem de vierkantswortel van het resultaat om a te vinden: √144 = 12
Dus, de lengte van de rechthoekszijde a is 12.
Belangrijke Aandachtspunten
- De stelling van Pythagoras geldt alleen voor rechthoekige driehoeken.
- Zorg ervoor dat je de juiste zijden identificeert (hypotenusa en rechthoekszijden).
- Wees voorzichtig met de eenheden. Alle lengtes moeten in dezelfde eenheid zijn gemeten (bijvoorbeeld centimeters, meters, inches).
Real-World Voorbeelden en Toepassingen
De stelling van Pythagoras is veel meer dan een abstracte wiskundige formule. Het heeft tal van praktische toepassingen in diverse gebieden:
Architectuur en Bouwkunde
Architecten en bouwkundigen gebruiken de stelling van Pythagoras om ervoor te zorgen dat gebouwen recht en stabiel zijn. Bijvoorbeeld, bij het leggen van funderingen of het construeren van daken wordt de stelling gebruikt om rechte hoeken te garanderen.
Voorbeeld: Een bouwvakker wil controleren of een hoek van een fundering recht is. Hij meet 3 meter langs de ene kant en 4 meter langs de andere kant. Als de diagonaal (de hypotenusa) precies 5 meter is, dan is de hoek een rechte hoek (32 + 42 = 52).
Navigatie
Navigators gebruiken de stelling van Pythagoras om afstanden te berekenen, vooral wanneer ze niet rechtlijnig kunnen reizen. Dit is relevant in de scheepvaart, luchtvaart en landnavigatie.
Voorbeeld: Een schip vaart 120 kilometer naar het oosten en vervolgens 50 kilometer naar het noorden. Om de kortste afstand tot het beginpunt te berekenen, kan de stelling van Pythagoras worden gebruikt: √(1202 + 502) ≈ 130 kilometer.
Constructie
De stelling wordt gebruikt bij de constructie van bruggen, tunnels en andere infrastructurele projecten. Het helpt om hoeken en afstanden te berekenen die cruciaal zijn voor de structurele integriteit.
Computergraphics en Spelontwikkeling
In de wereld van computerafbeeldingen en spelontwikkeling wordt de stelling van Pythagoras gebruikt om afstanden tussen objecten te berekenen. Dit is essentieel voor het bepalen van botsingen, het renderen van objecten en het simuleren van beweging.
Voorbeeld: In een videospel wil een programmeur bepalen of een personage dicht genoeg bij een object staat om ermee te interageren. De stelling van Pythagoras kan worden gebruikt om de afstand tussen het personage en het object te berekenen.
Landmeetkunde
Landmeters gebruiken de stelling om nauwkeurige metingen te verrichten en kaarten te maken. Het helpt bij het bepalen van de hoogte, afstand en hoeken in het landschap.
Veelgemaakte Fouten en Hoe Ze Te Vermijden
Hoewel de stelling van Pythagoras relatief eenvoudig is, zijn er enkele veelgemaakte fouten die je moet vermijden:
- Verkeerde Identificatie van de Hypotenusa: De hypotenusa is altijd de langste zijde en bevindt zich tegenover de rechte hoek.
- Verkeerde Formulegebruik: Zorg ervoor dat je de juiste formule gebruikt, afhankelijk van wat je wilt berekenen (a2 + b2 = c2 voor het berekenen van de hypotenusa, a2 = c2 - b2 voor het berekenen van een rechthoekszijde).
- Vergeten de Vierkantswortel te Nemen: Nadat je a2 + b2 hebt berekend, vergeet niet om de vierkantswortel te nemen om c te vinden.
- Verkeerde Eenheden: Gebruik altijd dezelfde eenheden voor alle zijden van de driehoek.
Conclusie
De stelling van Pythagoras is een krachtig en veelzijdig instrument met toepassingen die verder reiken dan de wiskundeles. Door de basisprincipes te begrijpen en te oefenen met verschillende scenario's, kun je deze stelling effectief gebruiken om problemen op te lossen in de wiskunde en in de echte wereld.
Oefen regelmatig met de stelling van Pythagoras, experimenteer met verschillende waarden en probeer de stelling toe te passen op problemen die je tegenkomt in je dagelijks leven. Daag jezelf uit! Hoe meer je oefent, hoe comfortabeler en bekwamer je zult worden in het gebruik van deze fundamentele wiskundige stelling.
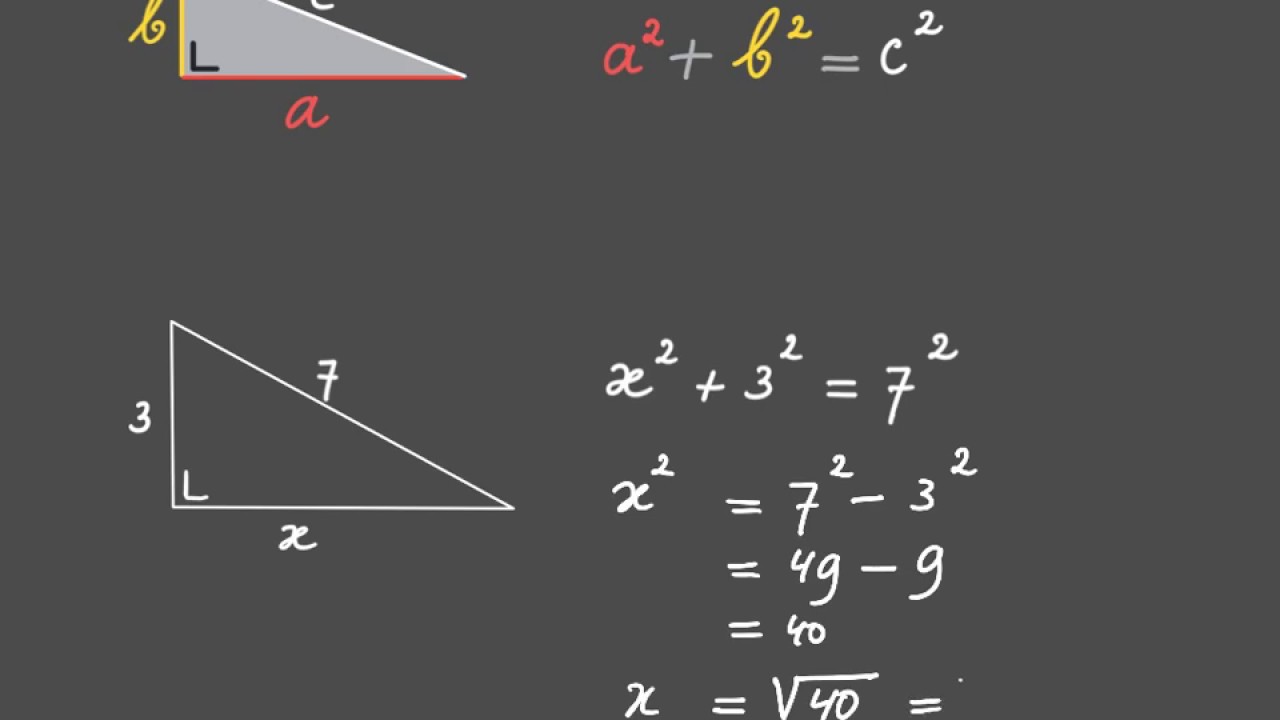
Bekijk ook deze gerelateerde berichten:
- Hoe Open Je Een Mail Zonder Naam
- Hoeveel Km Is Een M
- Erfenis Kleinkind Bij Overlijden Kind
- Wat Is Het Nationaal Inkomen
- Hoe Leer Je Voor Nederlands Examen
- Hoe Gaat Het In Duits
- Hoe Telt Het Combinatiecijfer Mee
- Hoeveel Kerken Zijn Er In Nederland
- Hoeveel Gaat Er Van Een Bruto Salaris Af
- Hoe Schrijf Je Een Datum In Cijfers
