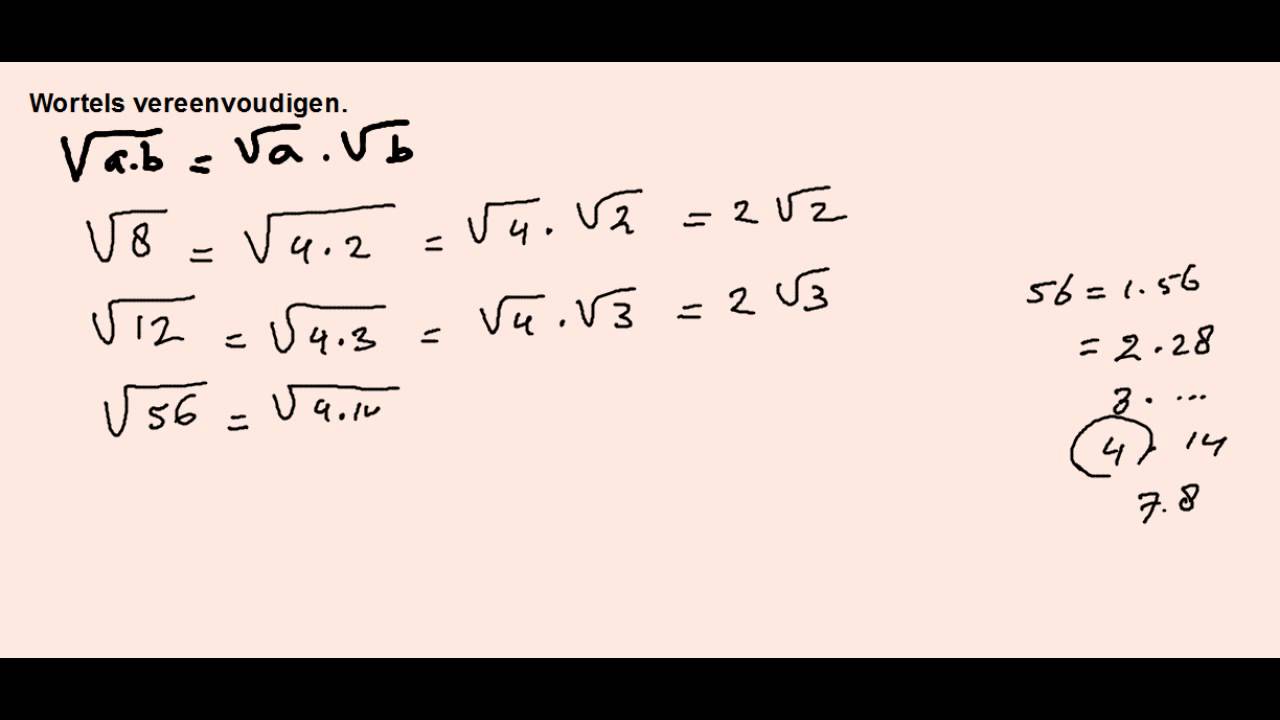Hoe Bereken Je De Wortel Van Een Getal

Heb je je ooit afgevraagd hoe je de wortel van een getal kunt berekenen zonder een rekenmachine? Of misschien ben je gewoon benieuwd naar de wiskunde achter deze fundamentele operatie? Dit artikel is speciaal voor jou, of je nu een student bent die worstelt met wiskunde, een ouder die je kind wil helpen, of gewoon iemand met een nieuwsgierige geest. We gaan samen op een reis om de geheimen van worteltrekken te ontsluieren! Verwacht geen ingewikkelde theorieën; we houden het simpel, praktisch en leuk.

Wat is een Wortel Eigenlijk?

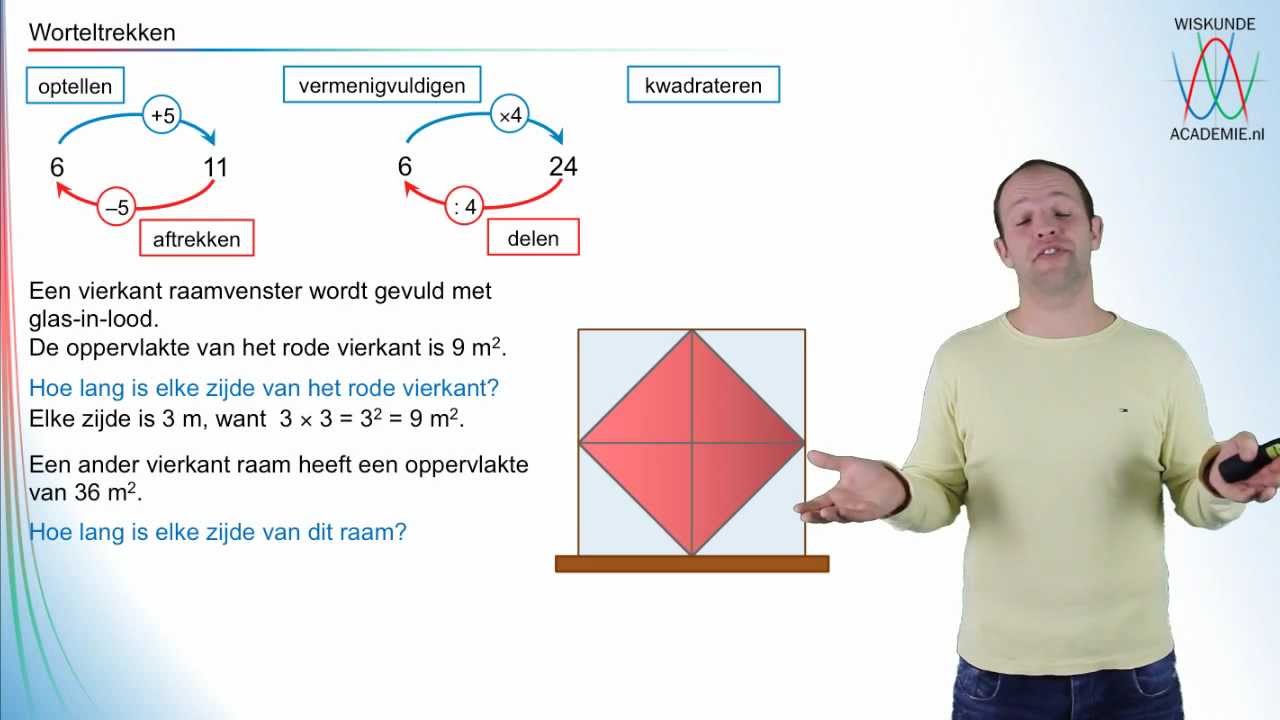
Voordat we in de berekeningen duiken, laten we eerst begrijpen wat een wortel precies is. Simpel gezegd, de wortel van een getal is een waarde die, vermenigvuldigd met zichzelf (voor een vierkantswortel), het oorspronkelijke getal oplevert. Denk aan een omgekeerde kwadraat.

Voorbeeld:

• De vierkantswortel van 9 is 3, omdat 3 * 3 = 9.
• De vierkantswortel van 25 is 5, omdat 5 * 5 = 25.

We gebruiken het √ symbool om de vierkantswortel aan te duiden. Dus √9 = 3.

Methoden om de Wortel te Berekenen

Er zijn verschillende manieren om de wortel van een getal te berekenen. Sommige zijn nauwkeuriger dan andere, en sommige zijn makkelijker te begrijpen. We zullen een paar populaire methoden bespreken:

1. Schatten en Verbeteren

Dit is een intuïtieve methode die goed werkt voor kleinere getallen. Het idee is om eerst een schatting te maken van de wortel, en die schatting vervolgens stapsgewijs te verbeteren.

Stappen:

1. Maak een schatting: Kies een getal dat volgens jou in de buurt komt van de wortel.
2. Deel: Deel het oorspronkelijke getal door je schatting.
3. Gemiddelde: Bereken het gemiddelde van je schatting en het resultaat van de deling. Dit is je nieuwe, verbeterde schatting.
4. Herhaal: Herhaal stap 2 en 3 totdat je een schatting hebt die nauwkeurig genoeg is.

Voorbeeld: Bereken de vierkantswortel van 10.

1. Schatting: We beginnen met 3 (omdat 3 * 3 = 9, wat dicht bij 10 ligt).
2. Delen: 10 / 3 = 3.33 (ongeveer)
3. Gemiddelde: (3 + 3.33) / 2 = 3.165 (ongeveer)
4. Herhaling:
   • 10 / 3.165 = 3.16 (ongeveer)
   • (3.165 + 3.16) / 2 = 3.1625 (ongeveer)

We kunnen nog een paar keer herhalen, maar 3.1625 is al een vrij nauwkeurige schatting van de vierkantswortel van 10. Een rekenmachine geeft ongeveer 3.1623.

2. De Babylonische Methode (Heron's Methode)

De Babylonische methode, ook wel bekend als Heron's methode, is een efficiëntere variant van de schat-en-verbeter methode. Het is een oude en verrassend snelle manier om de wortel van een getal te benaderen.

Formule:

x_n+1 = (x_n + S/x_n) / 2

Waarbij:

• S is het getal waarvan je de wortel wilt berekenen.
• x_n is je huidige schatting.
• x_n+1 is je volgende, verbeterde schatting.

Voorbeeld: Bereken de vierkantswortel van 2 (√2) met de Babylonische methode.

1. Initialisatie: We beginnen met een schatting. Laten we x₀ = 1 nemen.
2. Iteratie 1:
   • x₁ = (x₀ + S/x₀) / 2 = (1 + 2/1) / 2 = (1 + 2) / 2 = 3/2 = 1.5
3. Iteratie 2:
   • x₂ = (x₁ + S/x₁) / 2 = (1.5 + 2/1.5) / 2 = (1.5 + 1.333) / 2 = 2.833 / 2 = 1.4165
4. Iteratie 3:
   • x₃ = (1.4165 + 2/1.4165) / 2 = (1.4165 + 1.4118) / 2 = 2.8283 / 2 = 1.41415

Na slechts drie iteraties hebben we al een zeer nauwkeurige benadering van √2, namelijk 1.41415. De werkelijke waarde is ongeveer 1.41421.

3. Priemfactorisatie (Voor perfecte kwadraten)

Als je een perfecte kwadraat hebt (een getal dat het resultaat is van een getal vermenigvuldigd met zichzelf), kun je de wortel vinden door priemfactorisatie. Dit werkt echter alleen goed als het getal een perfecte kwadraat is.

Stappen:

1. Priemfactorisatie: Ontbind het getal in zijn priemfactoren.
2. Groepeer paren: Groepeer de priemfactoren in paren van dezelfde factoren.
3. Wortel berekenen: Neem één factor uit elk paar en vermenigvuldig deze met elkaar. Het resultaat is de wortel.

Voorbeeld: Bereken de vierkantswortel van 36.

1. Priemfactorisatie: 36 = 2 * 2 * 3 * 3
2. Groepeer paren: (2 * 2) * (3 * 3)
3. Wortel berekenen: 2 * 3 = 6

Dus de vierkantswortel van 36 is 6.

Waarom is dit Nuttig?

Je vraagt je misschien af: "Waarom zou ik dit allemaal leren? Ik heb toch een rekenmachine op mijn telefoon?" Dat is een goede vraag! Hoewel rekenmachines handig zijn, is het belangrijk om de basisprincipes achter de wiskunde te begrijpen. Dit helpt je om:

• Problemen beter te begrijpen: Je kunt complexere problemen beter analyseren en oplossen als je de basis begrijpt.
• Logisch te denken: Wiskunde bevordert logisch denken en probleemoplossende vaardigheden.
• Zelfvertrouwen op te bouwen: Het beheersen van wiskundige concepten geeft je een gevoel van voldoening en zelfvertrouwen.
• Rekenmachines te controleren: Je kunt je rekenmachine antwoorden controleren en fouten opsporen.

Praktische Toepassingen

Worteltrekken is niet alleen een abstract wiskundig concept. Het heeft veel praktische toepassingen in het dagelijks leven en in verschillende vakgebieden:

• Architectuur en Bouwkunde: Bij het berekenen van oppervlaktes, volumes en diagonale afstanden.
• Natuurkunde: Bij het berekenen van snelheden, versnellingen en energie.
• Computer Graphics: Bij het berekenen van afstanden en perspectieven in 3D-modellen.
• Financiën: Bij het berekenen van samengestelde interest en risico's.

Tips voor het Oefenen

Net als elke vaardigheid, vereist worteltrekken oefening. Hier zijn een paar tips om je te helpen:

• Begin met kleine getallen: Oefen eerst met het berekenen van de wortels van eenvoudige getallen zoals 4, 9, 16, 25, enz.
• Gebruik een rekenmachine om je antwoorden te controleren: Zo weet je of je het goed doet.
• Zoek patronen: Let op patronen in de getallen en hun wortels. Dit kan je helpen om sneller te rekenen.
• Maak het leuk: Maak er een spel van! Daag jezelf uit om de wortels van getallen in je omgeving te berekenen.
• Wees geduldig: Het kost tijd en moeite om worteltrekken te leren. Geef niet op als het niet meteen lukt.

Conclusie

Worteltrekken is een fundamentele wiskundige operatie met veel praktische toepassingen. Hoewel rekenmachines het gemakkelijk maken om wortels te berekenen, is het belangrijk om de principes erachter te begrijpen. Door de methoden te oefenen die we in dit artikel hebben besproken, kun je je wiskundige vaardigheden verbeteren en je zelfvertrouwen opbouwen. Dus ga aan de slag, experimenteer en ontdek de fascinerende wereld van de wiskunde! Vergeet niet: oefening baart kunst, en elke stap die je zet brengt je dichter bij je doel. Veel succes met het ontdekken van de wondere wereld van de wortels!