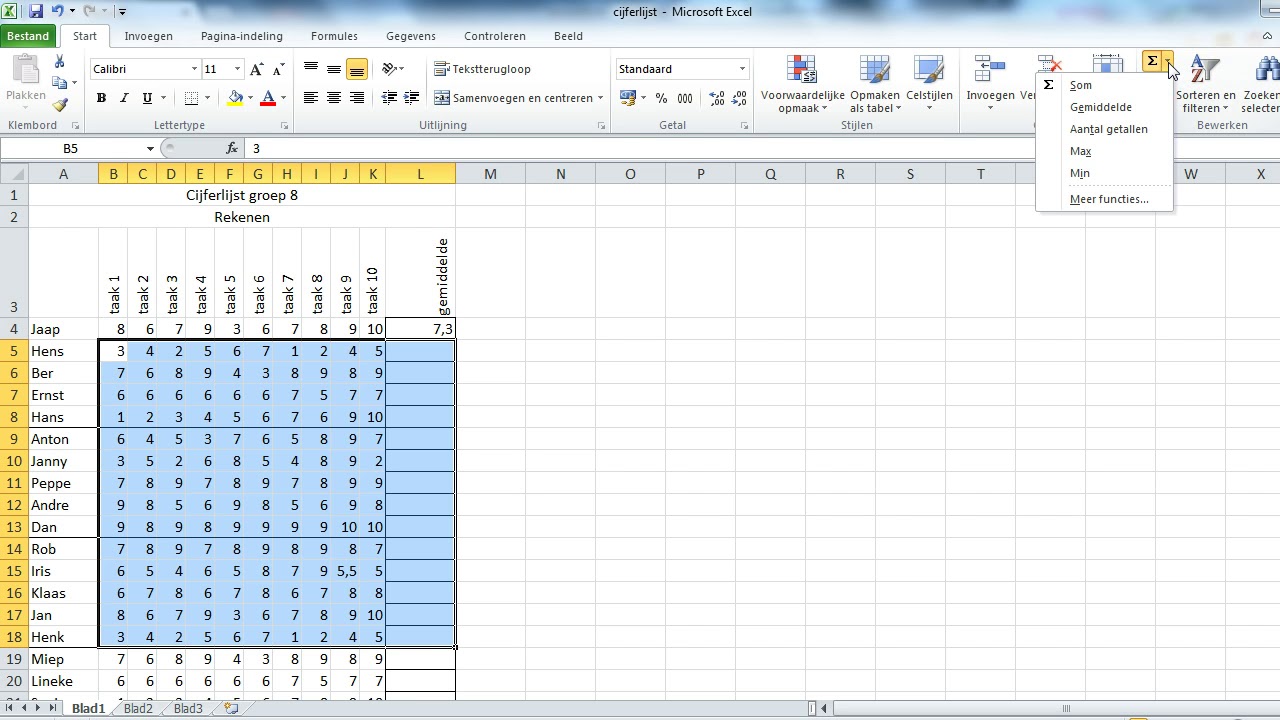
Hoe Bereken Je Een Gemiddelde Uit

Het gemiddelde, ook wel bekend als het rekenkundig gemiddelde, is een fundamenteel concept in de statistiek en data-analyse. Het biedt een manier om een centrale waarde te vinden die een representatie is van een reeks getallen. Het is een veelgebruikte methode in diverse disciplines, van financiën tot wetenschappelijk onderzoek en alledaagse besluitvorming.

Maar hoe bereken je nu precies zo'n gemiddelde, en wat zijn de nuances die daarbij komen kijken? In dit artikel zullen we de stappen uitleggen, illustraties geven met praktijkvoorbeelden en dieper ingaan op verschillende aspecten van de gemiddeldeberekening.

De Basisformule voor het Gemiddelde

De basisformule voor het berekenen van het gemiddelde is eigenlijk heel eenvoudig:

Gemiddelde = (Som van alle waarden) / (Aantal waarden)

Simpel gezegd: je telt alle getallen in een reeks op, en deelt die totale som door het aantal getallen dat je hebt opgeteld.

Stappenplan voor het Berekenen van een Gemiddelde

Identificeer de dataset: Verzamel alle getallen die je wilt gebruiken om het gemiddelde te berekenen. Dit kunnen bijvoorbeeld de resultaten van een examen, de dagelijkse temperatuurmetingen van een week, of de omzetcijfers van een bedrijf over een bepaald kwartaal zijn.
Bereken de som: Tel alle getallen in de dataset bij elkaar op. Zorg ervoor dat je nauwkeurig bent om fouten te voorkomen. Een rekenmachine kan hierbij een handig hulpmiddel zijn.
Tel het aantal waarden: Bepaal hoeveel getallen er in de dataset zitten. Dit is belangrijk om de som correct te kunnen delen.
Deel de som door het aantal waarden: Deel de totale som (stap 2) door het aantal waarden (stap 3). Het resultaat is het gemiddelde van de dataset.

Voorbeeld: Stel je voor dat je de volgende cijfers hebt gehaald voor je tentamens: 7, 8, 6, 9, 7. Om het gemiddelde te berekenen, tel je de cijfers bij elkaar op (7 + 8 + 6 + 9 + 7 = 37) en deel je dit door het aantal tentamens (5). Het gemiddelde is dus 37 / 5 = 7.4.

Wanneer is het Gemiddelde een Goede Representatie?

Hoewel het gemiddelde een handige maatstaf is, is het belangrijk om te onthouden dat het niet altijd een perfecte representatie van de data is. Het gemiddelde kan sterk beïnvloed worden door uitschieters, dit zijn extreme waarden die significant afwijken van de rest van de dataset.

Uitschieters en hun invloed: Stel je voor dat we het gemiddelde salaris van een klein bedrijf willen berekenen. De meeste werknemers verdienen tussen de €30.000 en €50.000 per jaar, maar de CEO verdient €500.000. Deze hoge waarde zal het gemiddelde salaris aanzienlijk verhogen, waardoor het een misleidend beeld geeft van wat de meeste werknemers verdienen. In zulke gevallen kan de mediaan (de middelste waarde) een betere maatstaf zijn voor de centrale tendentie.

Alternatieven voor het Gemiddelde: Mediaan en Modus

Naast het gemiddelde zijn er andere maatstaven voor centrale tendentie die in bepaalde situaties nuttiger kunnen zijn:

Mediaan: De mediaan is de middelste waarde in een geordende dataset. Om de mediaan te vinden, moet je de getallen eerst van klein naar groot sorteren. Als er een oneven aantal waarden is, is de mediaan het middelste getal. Als er een even aantal waarden is, is de mediaan het gemiddelde van de twee middelste getallen. De mediaan is minder gevoelig voor uitschieters dan het gemiddelde.
Modus: De modus is de waarde die het vaakst voorkomt in een dataset. Een dataset kan geen modus hebben, één modus (unimodaal), of meerdere modi (bimodaal, trimodaal, etc.). De modus is vooral nuttig voor categorische data (bijvoorbeeld, de meest voorkomende kleur auto in een bepaalde stad).

Gewogen Gemiddelde: Rekening houden met Belang

In sommige situaties zijn niet alle waarden even belangrijk. In dat geval is het gewogen gemiddelde een betere optie. Een gewogen gemiddelde houdt rekening met het gewicht of de belangrijkheid van elke waarde in de dataset.

Formule voor het Gewogen Gemiddelde:

Gewogen Gemiddelde = ( (Waarde 1 * Gewicht 1) + (Waarde 2 * Gewicht 2) + ... + (Waarde N * Gewicht N) ) / (Som van alle gewichten)

Voorbeeld: Stel dat je een cursus volgt waarbij je cijfer is gebaseerd op verschillende componenten: 40% voor tentamens, 30% voor opdrachten en 30% voor een presentatie. Je hebt een 7 gehaald voor de tentamens, een 8 voor de opdrachten en een 9 voor de presentatie. Het gewogen gemiddelde is dan: ( (7 * 0.40) + (8 * 0.30) + (9 * 0.30) ) / (0.40 + 0.30 + 0.30) = (2.8 + 2.4 + 2.7) / 1 = 7.9.

Dit gewogen gemiddelde geeft een nauwkeuriger beeld van je uiteindelijke cijfer dan een simpel gemiddelde, omdat het rekening houdt met de verschillende gewichten van de componenten.

Toepassingen van het Gewogen Gemiddelde

Beleggingen: Bij het berekenen van het rendement van een portefeuille wordt vaak een gewogen gemiddelde gebruikt, waarbij het gewicht van elke belegging wordt bepaald door de waarde van die belegging in de portefeuille.
Onderwijs: Zoals in het bovenstaande voorbeeld, wordt het gewogen gemiddelde vaak gebruikt om het eindcijfer van een cursus te berekenen, waarbij verschillende onderdelen van de cursus verschillende gewichten hebben.
Productie: Bij het berekenen van de gemiddelde productiekosten kan een gewogen gemiddelde worden gebruikt om rekening te houden met de verschillende hoeveelheden van verschillende grondstoffen.

Gemiddelde in Verschillende Contexten: Praktijkvoorbeelden

Het gemiddelde wordt in talloze situaties gebruikt. Hier zijn een paar voorbeelden:

Sport: Het gemiddelde aantal punten dat een basketballer per wedstrijd scoort, het gemiddelde aantal kilometers dat een wielrenner per etappe aflegt, of het gemiddelde aantal doelpunten dat een voetbalteam per seizoen maakt.
Economie: Het gemiddelde inkomen van een huishouden, de gemiddelde inflatievoet, of de gemiddelde groei van het bruto binnenlands product (BBP).
Weer: De gemiddelde temperatuur in een bepaalde maand, de gemiddelde neerslag in een jaar, of de gemiddelde windsnelheid op een bepaalde locatie.
Gezondheid: De gemiddelde levensverwachting, de gemiddelde bloeddruk, of de gemiddelde Body Mass Index (BMI).

Data Analyse: Stel je voor dat je de website data van je bedrijf wil analyseren. Je wil weten hoeveel tijd bezoekers gemiddeld op een bepaalde pagina besteden. Door alle sessietijden op die pagina bij elkaar op te tellen en dit te delen door het aantal sessies, krijg je de gemiddelde sessieduur. Dit kan je helpen om te bepalen of de content op die pagina aantrekkelijk is voor je bezoekers.

Kwaliteitscontrole: In een fabriek die onderdelen produceert, worden steekproeven genomen om de kwaliteit te controleren. Door de afmetingen van een aantal willekeurig gekozen onderdelen te meten en het gemiddelde te berekenen, kan men nagaan of de productie binnen de gestelde marges valt.

Aandachtspunten en Valstrikken

Ondanks de eenvoud van de formule, zijn er een paar dingen waar je op moet letten bij het berekenen en interpreteren van het gemiddelde:

Foutieve data: Zorg ervoor dat de data die je gebruikt correct is. Foutieve of onnauwkeurige data kan leiden tot een misleidend gemiddelde.
Representativiteit: Is de dataset representatief voor de populatie die je wilt analyseren? Als de dataset niet representatief is, kan het gemiddelde een vertekend beeld geven.
Interpretatie: Interpreteer het gemiddelde altijd in de context van de data. Houd rekening met uitschieters, de verdeling van de data en de aard van de variabele die je meet.
Significantie: Wees voorzichtig met het trekken van conclusies op basis van kleine verschillen in het gemiddelde. Bedenk of het verschil statistisch significant is en of het relevant is voor de praktijk.

Conclusie: Het Gemiddelde als Krachtig Instrument

Het berekenen van een gemiddelde is een fundamentele vaardigheid met brede toepassingen. Van het analyseren van sportprestaties tot het interpreteren van economische trends, het gemiddelde biedt een waardevolle samenvatting van een reeks getallen. Echter, het is cruciaal om de beperkingen van het gemiddelde te begrijpen en het te gebruiken in combinatie met andere statistische maatstaven om een compleet en accuraat beeld te krijgen.

Door de stappen in dit artikel te volgen en de aandachtspunten in acht te nemen, ben je goed uitgerust om het gemiddelde te berekenen en te interpreteren in diverse situaties. Blijf oefenen en experimenteren met verschillende datasets om je vaardigheden verder te ontwikkelen. Ga aan de slag en ontdek de kracht van het gemiddelde in jouw eigen data!