Hoe Bereken Je Een Hoek Met Tangens

Heb je ooit vastgezeten met een wiskundeprobleem waarbij je een hoek moest berekenen, maar je had alleen de lengte van de zijden van een rechthoekige driehoek? Geen paniek! De tangens (tan) functie kan je redder in nood zijn. Veel leerlingen vinden dit in eerste instantie lastig, maar met een heldere uitleg en wat oefening, wordt het een stuk eenvoudiger. Laten we samen duiken in de wereld van de tangens en ontdekken hoe je hiermee hoeken kunt berekenen.

Wat is Tangens eigenlijk?

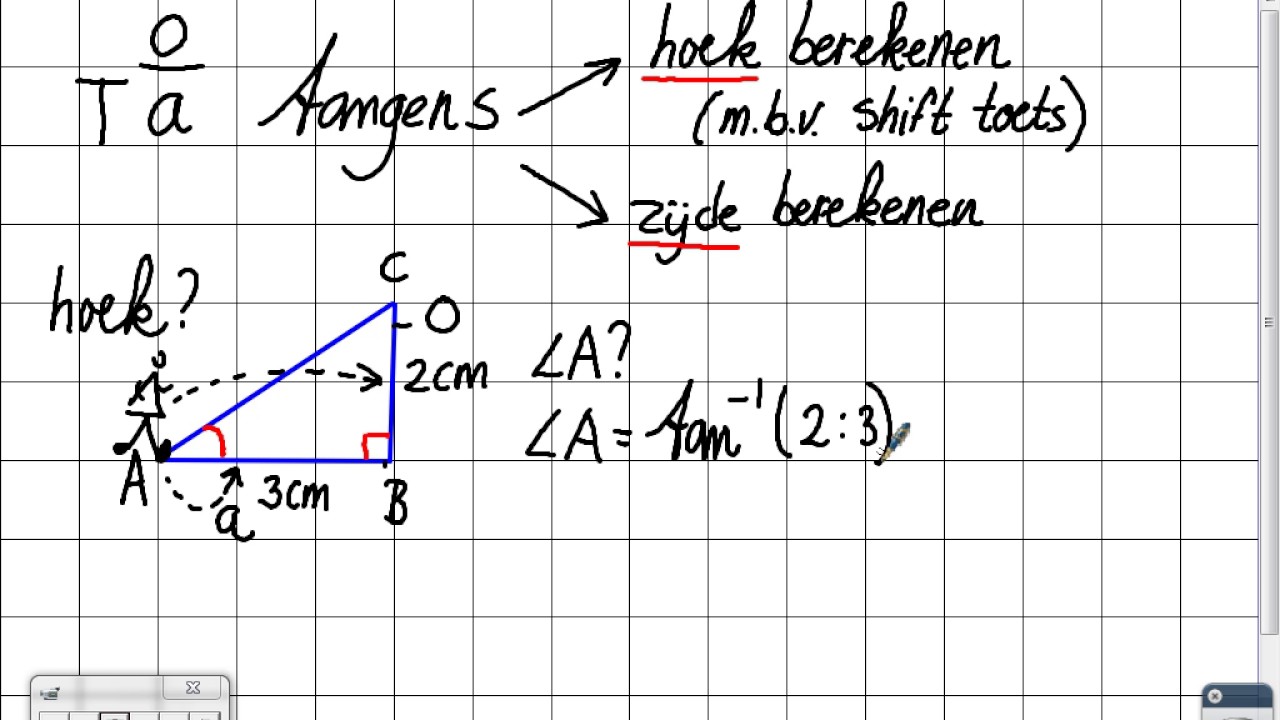
De tangens is een trigonometrische functie die de verhouding geeft tussen de overstaande zijde en de aanliggende zijde van een hoek in een rechthoekige driehoek. Let op: de tangens kan alleen gebruikt worden in rechthoekige driehoeken (een driehoek met een hoek van 90 graden).

Formule:

tan(hoek) = Overstaande zijde / Aanliggende zijde

Dit betekent dat, als je de lengte van de overstaande en aanliggende zijde kent, je de tangens van die hoek kunt berekenen. Maar wat als je de hoek zelf wilt weten?

De inverse tangens: jouw geheime wapen

Hier komt de inverse tangens, ook wel boogtangens of arctan genoemd, in beeld. De inverse tangens is de omgekeerde functie van de tangens. Het stelt je in staat om de hoek te berekenen als je de waarde van de tangens al weet. Met andere woorden, je vult de verhouding (overstaande/aanliggende) in, en de inverse tangens spuwt de hoek uit.

Formule:

hoek = arctan(Overstaande zijde / Aanliggende zijde)

Je kunt de inverse tangens functie vinden op de meeste wetenschappelijke rekenmachines. Vaak wordt deze aangegeven met tan^-1 of arctan.

Stappenplan voor het berekenen van een hoek met de tangens

Laten we het eens opsplitsen in een paar eenvoudige stappen:

1. Identificeer de rechthoekige driehoek: Zorg ervoor dat de driehoek die je bekijkt een rechte hoek heeft (90 graden).
2. Bepaal de overstaande en aanliggende zijde: Kijk vanuit de hoek die je wilt berekenen. De overstaande zijde is de zijde die recht tegenover de hoek ligt. De aanliggende zijde is de zijde die aan de hoek grenst (maar niet de schuine zijde).
3. Bereken de tangens: Deel de lengte van de overstaande zijde door de lengte van de aanliggende zijde.
4. Gebruik de inverse tangens (arctan): Gebruik de arctan functie op je rekenmachine om de hoek te vinden. Je moet meestal de "shift" of "2nd" knop indrukken om toegang te krijgen tot de arctan functie.
5. Controleer je antwoord: Zorg ervoor dat je antwoord logisch is. Hoeken in een rechthoekige driehoek moeten samen 180 graden zijn, en één hoek is al 90 graden.

Voorbeeld: Een ladder tegen een muur

Stel je voor: Een ladder van 5 meter lang staat tegen een muur. De voet van de ladder staat 2 meter van de muur. Welke hoek maakt de ladder met de grond?

In dit geval is de afstand van de muur tot de ladder (2 meter) de aanliggende zijde. De hoogte van de muur waar de ladder tegenaan leunt (die we nog niet weten, maar niet nodig hebben voor deze berekening!) zou de overstaande zijde zijn als we de hoek aan de top van de ladder zouden willen weten. Maar wij willen de hoek aan de onderkant weten, dus we moeten een beetje anders denken. We *kunnen* Pythagoras gebruiken om de hoogte van de muur te berekenen, maar er is een slimmere manier voor deze hoek:

Laten we *niet* de ladder zelf als een zijde van de driehoek beschouwen voor deze berekening. Stel je voor dat er een denkbeeldige verticale lijn loopt vanaf de top van de muur waar de ladder tegenaan leunt, recht naar beneden naar de grond, waar de voet van de ladder staat. Nu hebben we een perfecte rechthoekige driehoek!

Om de hoek te berekenen die de ladder met de grond maakt (noemen we die θ), denken we als volgt:

In *deze* context is het handiger om te focussen op de hoek bovenaan de ladder (de hoek tussen de ladder en de muur). We kunnen die hoek Φ noemen.

Dan:

Dus: tan(Φ) = 2 / h

En Φ = arctan(2/h)

Maar we zijn op zoek naar θ, niet Φ. We weten dat in een rechthoekige driehoek (en dit is een rechthoekige driehoek!), de twee niet-rechte hoeken samen 90 graden zijn. Dus:

θ + Φ = 90

Dus:

θ = 90 - Φ

θ = 90 - arctan(2/h)

Nu, om 'h' (de hoogte van de muur) te vinden, gebruiken we de stelling van Pythagoras: a² + b² = c²

Waarbij a = 2 (afstand tot de muur), b = h (hoogte van de muur), en c = 5 (lengte van de ladder)

Dus: 2² + h² = 5²

4 + h² = 25

h² = 21

h = √21 ≈ 4.58 meter

Nu kunnen we Φ berekenen:

Φ = arctan(2 / 4.58) ≈ arctan(0.4367) ≈ 23.6 graden

En uiteindelijk, de hoek die we echt wilden (θ):

θ = 90 - 23.6 ≈ 66.4 graden

De ladder maakt dus een hoek van ongeveer 66.4 graden met de grond.

Veelgemaakte fouten en hoe ze te vermijden

• Verkeerde zijden identificeren: Het is cruciaal om de overstaande en aanliggende zijde correct te identificeren, afhankelijk van de hoek die je wilt berekenen. Neem de tijd om dit goed te doen.
• Rekenmachine in verkeerde modus: Zorg ervoor dat je rekenmachine in de juiste modus staat (graden of radialen). Een verkeerde modus leidt tot een compleet verkeerd antwoord. De meeste wiskunde op school wordt in graden gedaan, dus controleer dit dubbel.
• Vergeten de inverse tangens te gebruiken: Je berekent de *verhouding* met tangens, maar je hebt de *inverse* tangens nodig (arctan) om de hoek zelf te vinden.

Wanneer gebruik je tangens (en wanneer niet)?

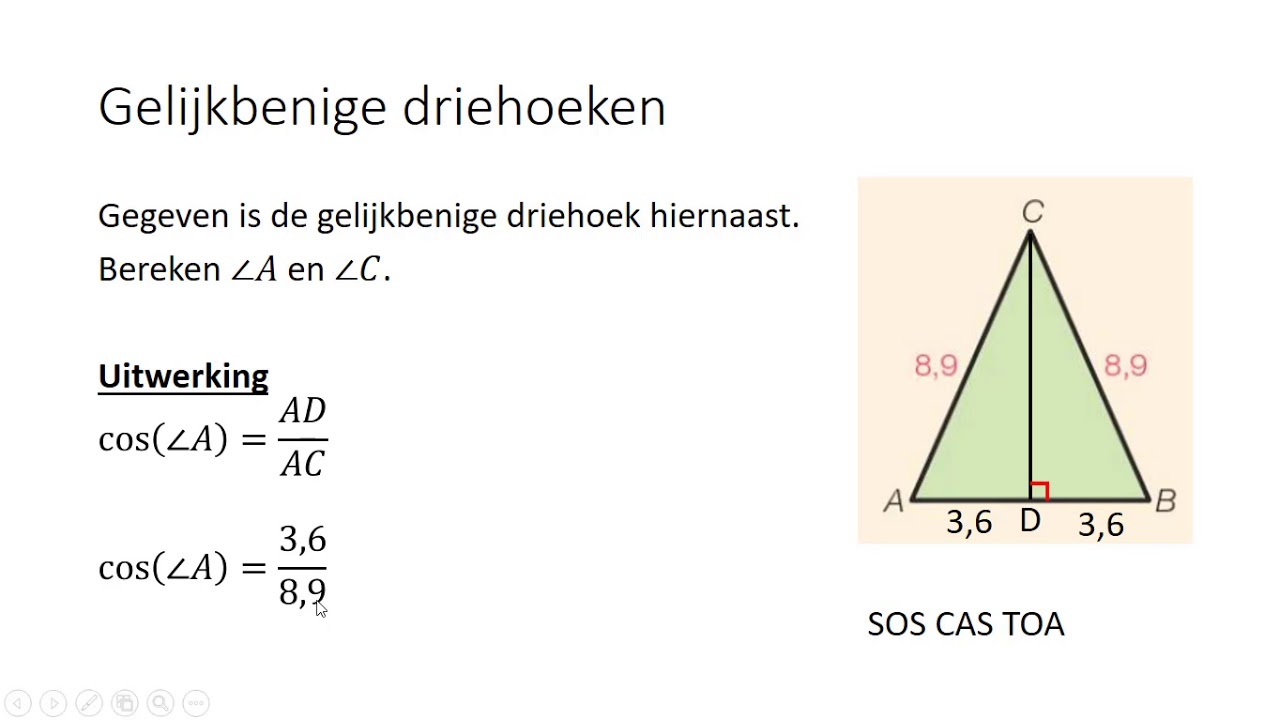
De tangens is perfect voor het berekenen van hoeken in een rechthoekige driehoek als je de lengte van de overstaande en aanliggende zijde kent. Als je de lengte van de schuine zijde kent, kun je beter de sinus (sin) of cosinus (cos) gebruiken.

Tangens in het echte leven

De tangens is niet alleen een abstract wiskundig concept. Het wordt in talloze praktische situaties gebruikt:

Oefening baart kunst

De beste manier om de tangens en de inverse tangens onder de knie te krijgen, is door te oefenen. Zoek online naar oefenopgaven, of bedenk zelf voorbeelden. Hoe meer je oefent, hoe zelfverzekerder je zult worden in het berekenen van hoeken met de tangens.

Hopelijk heeft deze uitleg je geholpen om de tangens en de inverse tangens beter te begrijpen. Ga aan de slag, oefen veel, en binnenkort bereken je hoeken alsof het niets is!