Hoe Bereken Je Oppervlakte Driehoek

Het berekenen van de oppervlakte van een driehoek is een fundamentele vaardigheid in de geometrie, met toepassingen die zich uitstrekken van de wiskundeles tot praktische situaties in de architectuur, engineering en zelfs het dagelijks leven. Hoewel de basisformule eenvoudig lijkt, is het belangrijk om de verschillende methoden te begrijpen en te weten wanneer welke methode het meest geschikt is. Deze artikel zal een diepgaand overzicht geven van de verschillende manieren om de oppervlakte van een driehoek te berekenen, inclusief uitgebreide uitleg en voorbeelden om je begrip te versterken.

Verschillende Methoden om de Oppervlakte van een Driehoek te Berekenen

Er zijn verschillende formules die gebruikt kunnen worden om de oppervlakte van een driehoek te berekenen. De meest bekende is wellicht de formule gebaseerd op de basis en de hoogte, maar er zijn ook andere methoden, zoals de formule van Heron en trigonometrische benaderingen. De keuze van de methode hangt af van de informatie die je over de driehoek hebt.

De Basis-Hoogte Formule: De Meest Bekende Methode

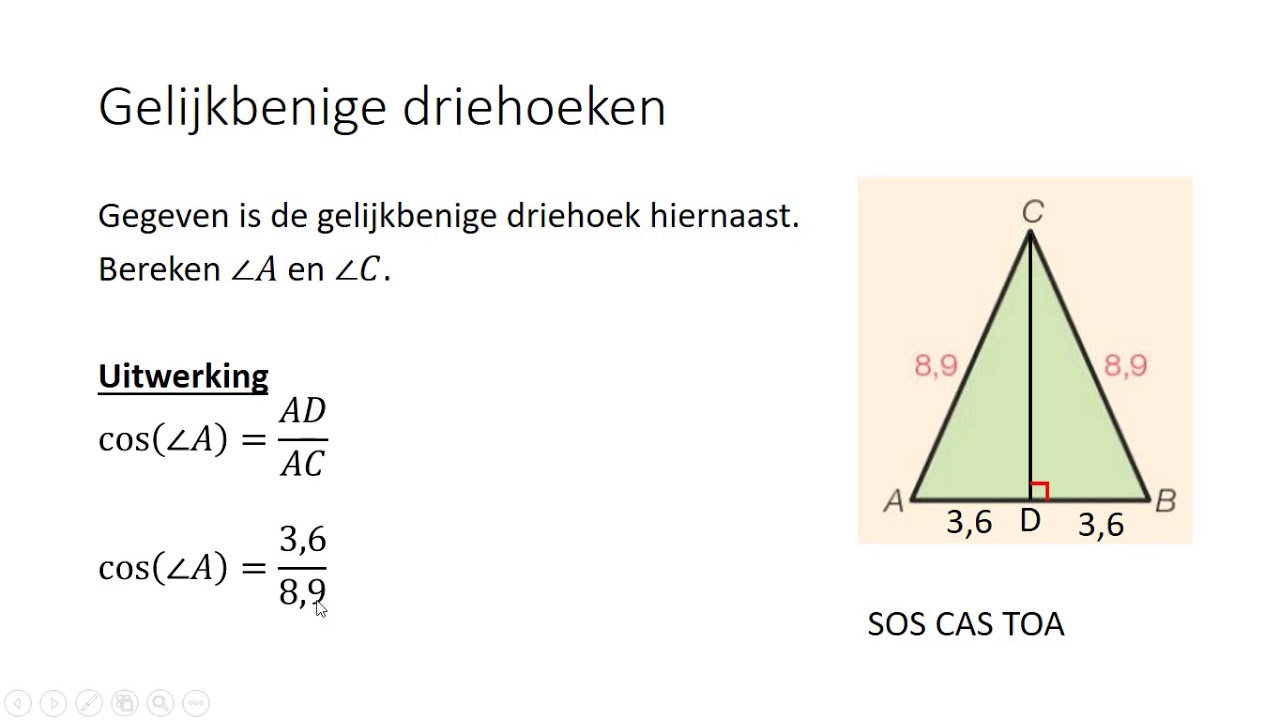
De meest gebruikte formule voor het berekenen van de oppervlakte van een driehoek is: Oppervlakte = (1/2) * basis * hoogte. Hierbij is de basis (b) de lengte van een van de zijden van de driehoek, en de hoogte (h) is de loodrechte afstand van de tegenoverliggende hoekpunt tot de basis. Het is essentieel dat de hoogte loodrecht staat op de basis; een schuine lijn is geen geldige hoogte.

Voorbeeld: Stel je voor dat je een driehoek hebt met een basis van 8 cm en een hoogte van 5 cm. De oppervlakte zou dan zijn: (1/2) * 8 cm * 5 cm = 20 cm². Dit betekent dat de driehoek een oppervlakte heeft van 20 vierkante centimeter.

Het identificeren van de juiste hoogte kan soms lastig zijn, vooral bij stomphoekige driehoeken (driehoeken met een hoek groter dan 90 graden). In dat geval kan de hoogte buiten de driehoek vallen. Het is cruciaal om te visualiseren of te construeren hoe de loodrechte lijn van het hoekpunt op de basis (of de verlenging daarvan) valt.

De Formule van Heron: Wanneer de Zijden Bekend Zijn

Als je de lengtes van de drie zijden van een driehoek kent, maar geen hoogte, dan is de formule van Heron een handige tool. Deze formule maakt gebruik van de semiperimeter (s) van de driehoek, die de helft is van de omtrek: s = (a + b + c) / 2, waarbij a, b en c de lengtes van de zijden zijn. De oppervlakte wordt dan berekend met de volgende formule: Oppervlakte = √(s * (s - a) * (s - b) * (s - c)).

Voorbeeld: Een driehoek heeft zijden van 5 cm, 7 cm en 8 cm. De semiperimeter is s = (5 + 7 + 8) / 2 = 10 cm. De oppervlakte is dan √(10 * (10 - 5) * (10 - 7) * (10 - 8)) = √(10 * 5 * 3 * 2) = √300 ≈ 17.32 cm².

De formule van Heron is bijzonder nuttig in situaties waar het moeilijk is om de hoogte direct te meten, bijvoorbeeld bij landmetingen of constructies waarbij alleen de zijlengtes bekend zijn.

Trigonometrie: Werken met Hoeken en Zijden

Als je de lengte van twee zijden van een driehoek en de hoek daartussen (ingesloten hoek) kent, kun je de oppervlakte berekenen met behulp van trigonometrie. De formule is: Oppervlakte = (1/2) * a * b * sin(C), waarbij a en b de lengtes van de twee zijden zijn en C de hoek is tussen deze zijden.

Voorbeeld: Stel dat je een driehoek hebt met zijden van 6 cm en 9 cm, en de ingesloten hoek is 60 graden. De oppervlakte zou dan zijn: (1/2) * 6 cm * 9 cm * sin(60°) = (1/2) * 6 cm * 9 cm * (√3/2) ≈ 23.38 cm².

Het begrijpen van trigonometrische functies, zoals de sinus (sin), is essentieel voor het gebruik van deze methode. Deze methode is vooral handig bij het werken met schuine driehoeken, waar de basis-hoogte methode minder direct toepasbaar is.

Coördinaat Geometrie: Werken met Punten in een Vlak

Als de hoekpunten van de driehoek gegeven zijn als coördinaten in een vlak (bijvoorbeeld (x1, y1), (x2, y2), en (x3, y3)), dan kan de oppervlakte worden berekend met behulp van de volgende formule: Oppervlakte = (1/2) * |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|. De verticale strepen geven de absolute waarde aan, wat betekent dat de uitkomst altijd positief is.

Voorbeeld: Beschouw een driehoek met hoekpunten (1, 2), (4, 6) en (7, 3). De oppervlakte is (1/2) * |1(6 - 3) + 4(3 - 2) + 7(2 - 6)| = (1/2) * |3 + 4 - 28| = (1/2) * |-21| = 10.5 eenheden².

Deze methode is bijzonder nuttig in de cartesiaanse meetkunde en bij het werken met digitale afbeeldingen en computer graphics.

Real-World Voorbeelden en Toepassingen

De berekening van de oppervlakte van een driehoek is niet alleen een theoretische oefening. Het heeft talloze praktische toepassingen in verschillende vakgebieden:

Data Voorbeeld: Stel dat een architect een driehoekig raam ontwerpt voor een modern huis. De basis van het raam is 3 meter en de hoogte is 1.5 meter. De oppervlakte van het raam is (1/2) * 3 m * 1.5 m = 2.25 m². Dit helpt de architect om de juiste hoeveelheid glas te bestellen en de kosten te schatten.

Conclusie en Oproep tot Actie

Het berekenen van de oppervlakte van een driehoek is een essentiële vaardigheid met een breed scala aan toepassingen. Door de verschillende methoden te begrijpen, zoals de basis-hoogte formule, de formule van Heron, trigonometrische benaderingen en de methode met coördinaten, kun je de oppervlakte van een driehoek berekenen, ongeacht de beschikbare informatie. Oefening baart kunst, dus probeer verschillende voorbeelden en scenario's om je vaardigheden te verbeteren.

Neem de tijd om de besproken methoden te oefenen met verschillende voorbeelden. Zoek online bronnen, leerboeken of oefenopgaven om je kennis verder te verdiepen. Het beheersen van deze vaardigheid zal je niet alleen helpen bij wiskundige problemen, maar ook in praktische situaties waar geometrie een rol speelt. Experimenteer met verschillende soorten driehoeken en gegevens om je vertrouwdheid met de methoden te vergroten. Daag jezelf uit!

Blijf leren en ontdekken de fascinerende wereld van de geometrie!