Hoe Bereken Je Oppervlakte Van Een Driehoek

Heb je ooit naar een driehoek gekeken en je afgevraagd, "Hoe bereken ik de oppervlakte hiervan?" Je bent niet alleen. Veel mensen, van studenten tot hobbyisten, vinden het berekenen van de oppervlakte van een driehoek lastig. Maar geen zorgen, deze gids maakt het gemakkelijk en begrijpelijk!

Waarom is dit belangrijk? De oppervlakte van een driehoek berekenen is niet zomaar een wiskunde-oefening. Het is een praktische vaardigheid die je kunt gebruiken in de bouw, landmeetkunde, kunst, en zelfs bij het plannen van je tuin. Stel je voor dat je een zeil voor je boot moet maken, een dak moet ontwerpen, of een stuk land moet verdelen. In al deze situaties komt de kennis van de oppervlakte van een driehoek goed van pas.

De Basis: Hoogte en Basis

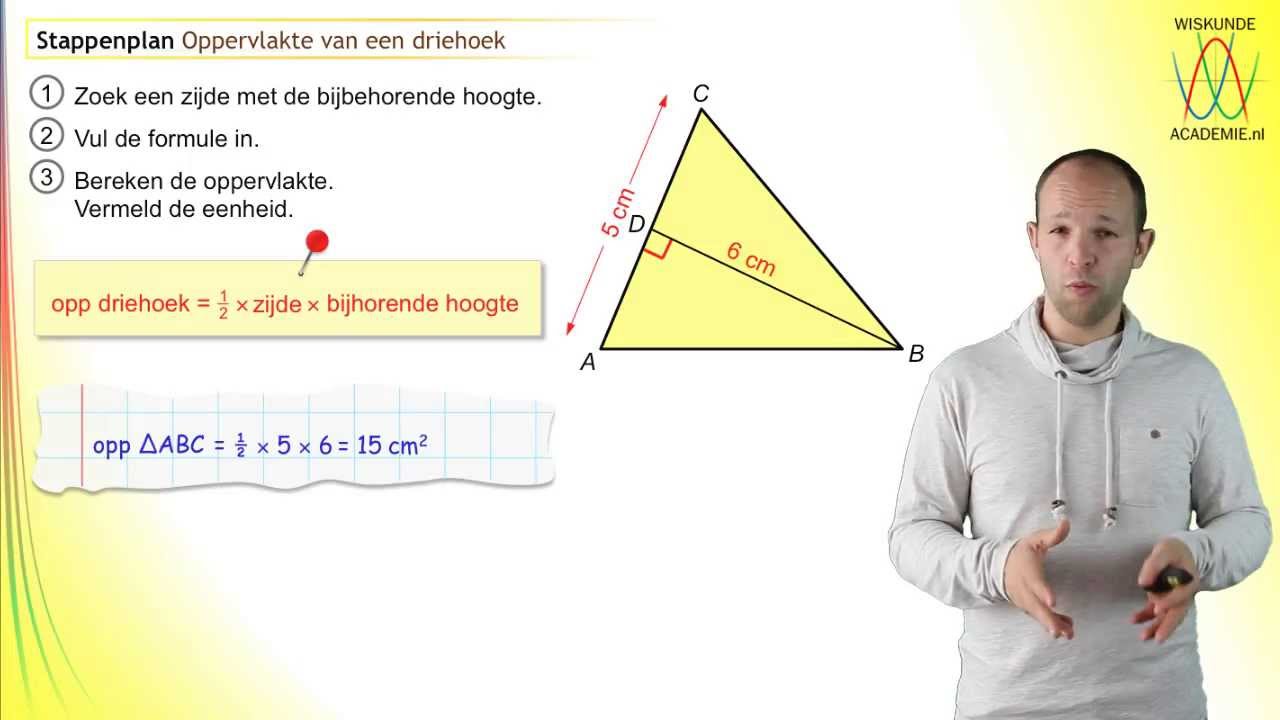
De meest bekende formule voor de oppervlakte van een driehoek is: Oppervlakte = ½ * basis * hoogte. Laten we dit even uitpakken.

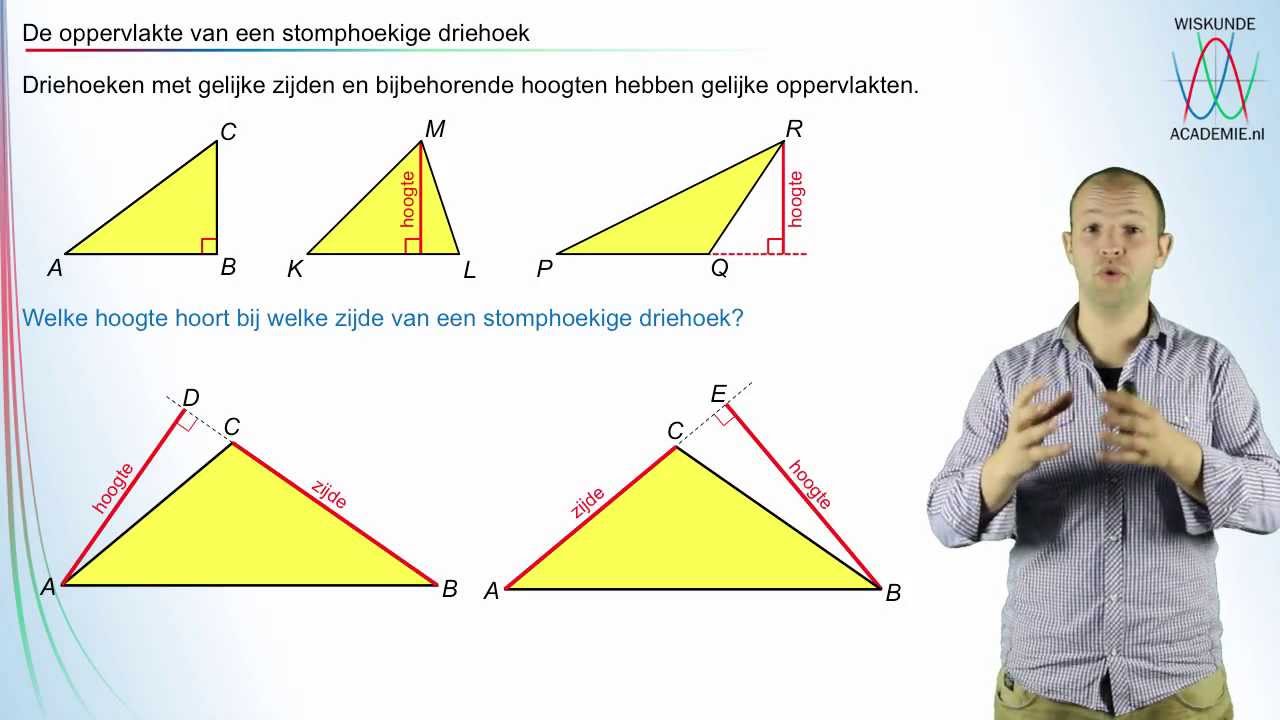
De basis is een van de zijden van de driehoek. Het maakt niet uit welke zijde je kiest, zolang je de bijbehorende hoogte maar kent.

De hoogte is de loodrechte afstand van de basis tot de tegenoverliggende hoek (het hoekpunt). Stel je voor dat je een lijn trekt van het hoekpunt recht naar beneden (in een rechte hoek) op de basis. De lengte van deze lijn is de hoogte.

Voorbeeld: Stel dat een driehoek een basis heeft van 8 cm en een hoogte van 5 cm. De oppervlakte is dan ½ * 8 cm * 5 cm = 20 cm². Vergeet niet de eenheden te gebruiken! De oppervlakte wordt altijd uitgedrukt in vierkante eenheden (cm², m², etc.).

Dit lijkt eenvoudig, maar wat als je de hoogte niet direct weet? Gelukkig zijn er andere methoden!

De Formule van Heron: Als Je Alle Zijden Kent

De formule van Heron is een krachtige tool als je de lengte van alle drie de zijden van de driehoek kent (a, b, en c), maar niet de hoogte. De formule ziet er misschien intimiderend uit, maar is eigenlijk heel rechttoe rechtaan:

Oppervlakte = √[s(s-a)(s-b)(s-c)]

Waar:

s = (a + b + c) / 2 (s is de halve omtrek van de driehoek)

Laten we dit illustreren met een voorbeeld:

Stel, een driehoek heeft zijden van 5 cm, 7 cm, en 8 cm.

1. Bereken s: s = (5 + 7 + 8) / 2 = 10 cm
2. Pas de formule van Heron toe: Oppervlakte = √[10(10-5)(10-7)(10-8)] = √[10 * 5 * 3 * 2] = √300 ≈ 17.32 cm²

Dus de oppervlakte van de driehoek is ongeveer 17.32 cm². De formule van Heron is vooral handig bij onregelmatige driehoeken waar het moeilijk is om de hoogte te bepalen.

Trigonometrie Redt de Dag: Twee Zijden en een Ingesloten Hoek

Soms weet je de lengte van twee zijden van een driehoek (a en b) en de ingesloten hoek (de hoek tussen die twee zijden, laten we die γ noemen). In dit geval kun je trigonometrie gebruiken!

Oppervlakte = ½ * a * b * sin(γ)

Sin(γ) is de sinus van de hoek γ. Je kunt dit berekenen met een wetenschappelijke rekenmachine of een online sinus calculator.

Voorbeeld: Een driehoek heeft zijden van 6 cm en 9 cm, en de ingesloten hoek is 60 graden.

1. Bereken sin(60°): sin(60°) ≈ 0.866
2. Pas de formule toe: Oppervlakte = ½ * 6 cm * 9 cm * 0.866 ≈ 23.38 cm²

De oppervlakte is ongeveer 23.38 cm². Deze methode is essentieel in de landmeetkunde en navigatie, waar hoeken en afstanden vaak de primaire meetwaarden zijn.

Speciale Gevallen: Rechthoekige Driehoeken

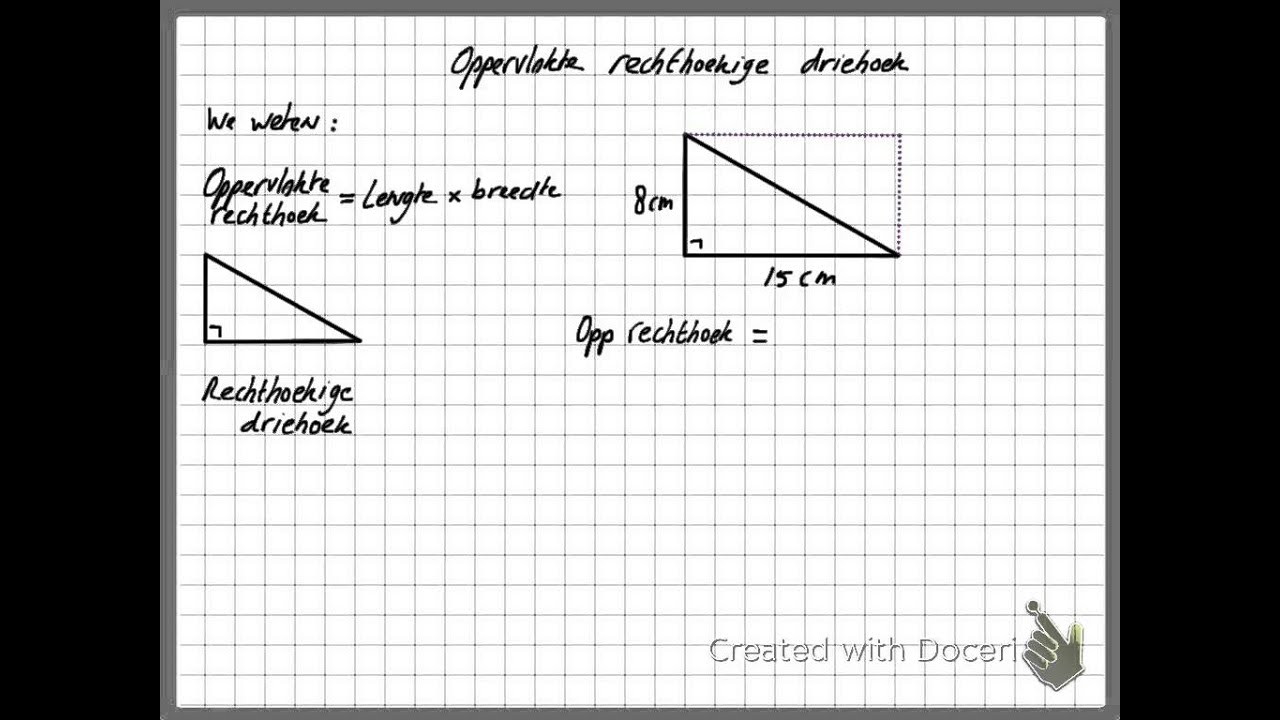
Rechthoekige driehoeken zijn bijzonder omdat de hoogte en de basis al duidelijk gedefinieerd zijn! In een rechthoekige driehoek zijn de twee zijden die de rechte hoek vormen (de rechthoekszijden) de basis en de hoogte. Je hoeft dus geen extra berekeningen te doen om de hoogte te vinden.

Oppervlakte (rechthoekige driehoek) = ½ * rechthoekszijde 1 * rechthoekszijde 2

Voorbeeld: Een rechthoekige driehoek heeft rechthoekszijden van 3 cm en 4 cm. De oppervlakte is ½ * 3 cm * 4 cm = 6 cm².

Rechthoekige driehoeken zijn veelvoorkomend in constructie en architectuur, waardoor het berekenen van hun oppervlakte een essentiële vaardigheid is.

Een paar extra tips:

• Consistentie in eenheden: Zorg ervoor dat je alle metingen in dezelfde eenheden hebt voordat je gaat rekenen. Als je bijvoorbeeld de basis in meters hebt en de hoogte in centimeters, moet je ze eerst converteren naar dezelfde eenheid (bijvoorbeeld beide in meters).
• Gebruik een rekenmachine: Voor ingewikkelde berekeningen, vooral bij het gebruik van de formule van Heron of trigonometrie, is een wetenschappelijke rekenmachine onmisbaar.
• Controleer je antwoord: Nadat je de oppervlakte hebt berekend, denk dan even na of het antwoord logisch is. Een erg kleine oppervlakte voor een grote driehoek is waarschijnlijk een fout.

Waarom deze formules werken: Een korte uitleg

Het begrijpen van de logica achter de formules helpt om ze beter te onthouden en toe te passen. De formule ½ * basis * hoogte is gebaseerd op het idee dat een driehoek precies de helft is van een rechthoek (of parallellogram) met dezelfde basis en hoogte. Stel je voor dat je een identieke driehoek er tegenaan plakt - je krijgt dan een rechthoek!

De formule van Heron is afgeleid van de stelling van Pythagoras en trigonometrische identiteiten. De details zijn wat complexer, maar het komt erop neer dat de formule een slimme manier is om de hoogte te berekenen indirect, alleen met de lengtes van de zijden.

De trigonometrische formule (½ * a * b * sin(γ)) is gebaseerd op de definitie van de sinus van een hoek in een rechthoekige driehoek en de relatie tussen de hoogte, de zijde en de hoek. Je kunt de hoogte van de driehoek uitdrukken als b * sin(γ), en dit invullen in de basisformule.

Praktische toepassingen: Meer dan alleen schoolwerk

Zoals eerder genoemd, is het berekenen van de oppervlakte van een driehoek niet alleen theorie. Hier zijn een paar concrete voorbeelden:

• Landmeetkunde: Landmeters gebruiken driehoeksmeting om de oppervlakte van percelen land te bepalen.
• Constructie: Architecten en bouwkundigen gebruiken driehoeken in dakconstructies, bruggen en andere structuren. Het berekenen van de oppervlakte is cruciaal voor het bepalen van de hoeveelheid materialen die nodig zijn.
• Zeilen: Zeilmakers moeten de oppervlakte van zeilen berekenen om de juiste hoeveelheid doek te bepalen en de prestaties van het zeil te optimaliseren.
• Design: Grafisch ontwerpers en interieurarchitecten gebruiken driehoeken vaak in hun ontwerpen. Het kennen van de oppervlakte helpt bij het creëren van evenwichtige en esthetisch aantrekkelijke composities.
• Tuinieren: Bij het plannen van een tuin kan het handig zijn om de oppervlakte van driehoekige plantenbedden te berekenen om te bepalen hoeveel aarde, mest of planten je nodig hebt.

Een real-life voorbeeld: Stel je voor dat je een schaduwdoek wilt ophangen in je tuin. Je hebt drie bevestigingspunten, die een driehoek vormen. Om de juiste maat doek te bestellen, moet je de oppervlakte van die driehoek berekenen. Door de afstand tussen de bevestigingspunten te meten (de zijden van de driehoek) en de formule van Heron te gebruiken, kun je de benodigde oppervlakte bepalen en de perfecte schaduwdoek bestellen.

Conclusie: Oefening Baart Kunst!

Het berekenen van de oppervlakte van een driehoek is een waardevolle vaardigheid met toepassingen in veel verschillende gebieden. Of je nu een student bent, een professional, of gewoon iemand die graag klust, het begrijpen van deze formules zal je zeker van pas komen. Oefening baart kunst! Probeer verschillende voorbeelden uit, experimenteer met verschillende methoden, en voor je het weet, bereken je de oppervlakte van een driehoek zonder erover na te denken. Onthoud: begin met de basis, begrijp de formules, en pas ze toe in de praktijk! Succes!