Hoe Deel Je Een Breuk
Heb je ooit voor de uitdaging gestaan een pizza eerlijk te verdelen over een groep vrienden, maar de stukken waren al in ongelijke delen gesneden? Of probeerde je een recept te halveren dat aangeeft hoeveel 1/3 kopje van een ingrediënt nodig is? Dan weet je al dat het begrijpen van breuken en het kunnen delen ervan, van onschatbare waarde is in het dagelijks leven! Deze handleiding is speciaal geschreven voor jou: de leerling, de hobbykok, de klusser - iedereen die wil leren hoe je breuken deelt, op een heldere en eenvoudige manier.
Waarom is het Delen van Breuken Belangrijk?
Het delen van breuken lijkt misschien een abstract wiskundig concept, maar de toepassingen zijn verrassend praktisch. Denk aan:
- Recepten aanpassen: Je hebt een recept voor een taart, maar wilt slechts de helft maken. Je moet dan alle hoeveelheden delen, inclusief diegene die als breuk staan.
- Bouwprojecten: Een plank moet in gelijke stukken worden gezaagd, maar de lengte is uitgedrukt in een breuk.
- Financiën: Een bepaald percentage van je inkomen (een breuk) moet worden verdeeld over verschillende spaarrekeningen.
- Tijdmanagement: Je hebt 2/3 van een uur om 5 taken te voltooien. Hoeveel tijd heb je per taak?
Door het delen van breuken te beheersen, vergroot je je probleemoplossend vermogen en voel je je zekerder in situaties die een beroep doen op wiskundige vaardigheden.
De Basis: Wat zijn Breuken Eigenlijk?
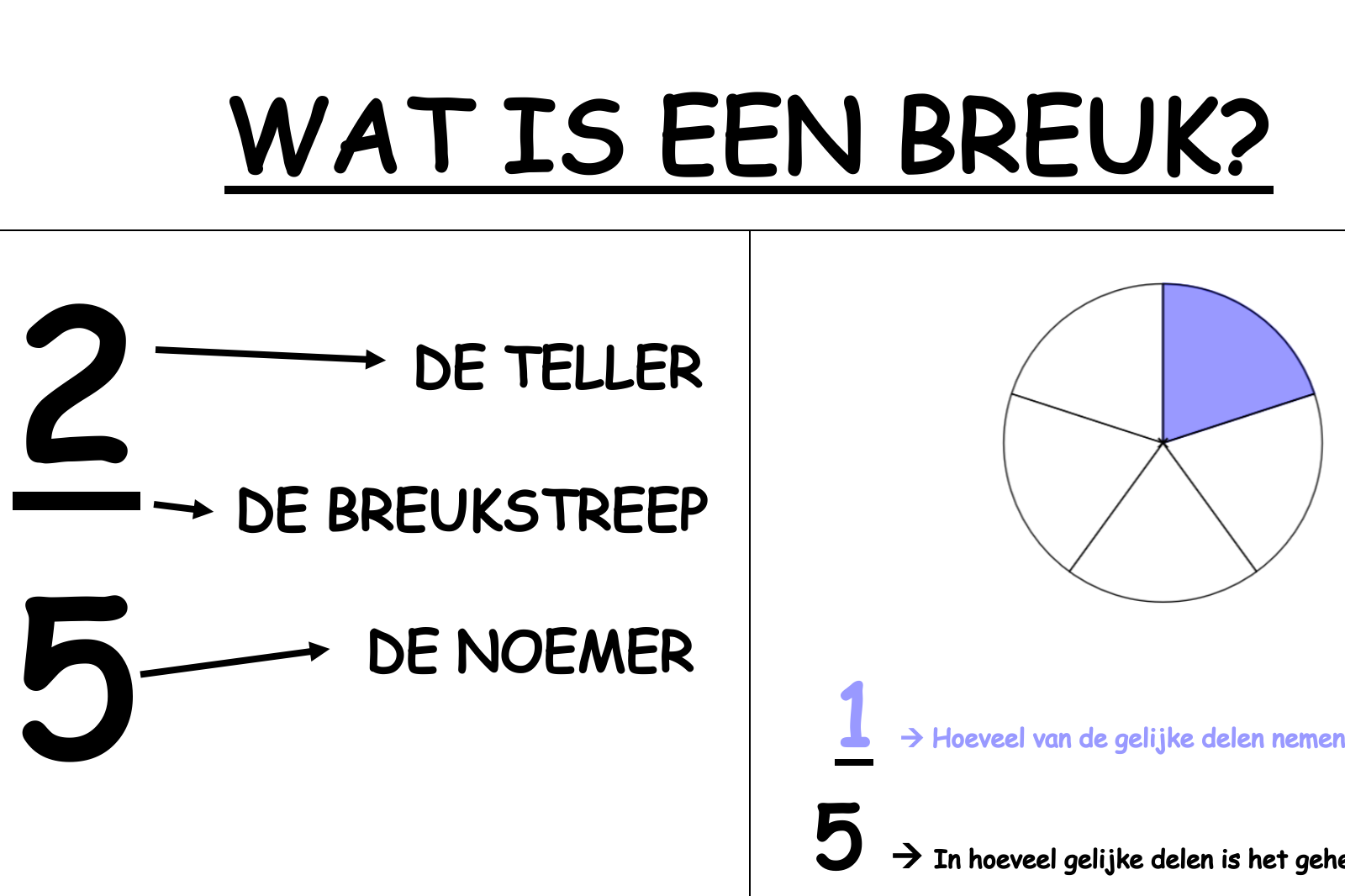
Laten we eerst de basis herhalen. Een breuk bestaat uit twee delen:
- De teller (bovenste getal): Geeft aan hoeveel delen we hebben.
- De noemer (onderste getal): Geeft aan in hoeveel gelijke delen het geheel is verdeeld.
Bijvoorbeeld, de breuk 3/4 betekent dat we 3 delen hebben van een geheel dat in 4 gelijke delen is verdeeld. Denk aan een pizza die in vier stukken is gesneden, waarvan je er drie opeet.
Soorten Breuken
Er zijn verschillende soorten breuken, waaronder:
- Echte breuken: De teller is kleiner dan de noemer (bijv. 1/2, 2/3, 5/8).
- Onechte breuken: De teller is groter dan of gelijk aan de noemer (bijv. 5/4, 7/3, 3/3).
- Gemengde getallen: Bestaan uit een geheel getal en een echte breuk (bijv. 1 1/2, 2 3/4).
Het is belangrijk om te weten dat je onechte breuken kunt omzetten in gemengde getallen en vice versa. Dit is cruciaal bij het delen van breuken.
Het Delen van Breuken: Stap voor Stap
Nu komen we tot de kern: hoe deel je breuken? De sleutel is een simpele regel: "Keer om en vermenigvuldig!".
Dit betekent dat je de tweede breuk (de breuk waarmee je deelt) omkeert (de teller en noemer verwisselt) en vervolgens de eerste breuk vermenigvuldigt met de omgekeerde tweede breuk.
Laten we dit stap voor stap bekijken met een voorbeeld: 1/2 ÷ 1/4.
- Stap 1: Keer de tweede breuk om (neem de reciproke). De reciproke van 1/4 is 4/1.
- Stap 2: Vermenigvuldig de eerste breuk met de reciproke van de tweede breuk. 1/2 x 4/1 = (1 x 4) / (2 x 1) = 4/2.
- Stap 3: Vereenvoudig de breuk indien mogelijk. 4/2 kan vereenvoudigd worden tot 2. Dus, 1/2 ÷ 1/4 = 2.
Voorbeelden met Uitleg
Laten we enkele voorbeelden bekijken om dit concept verder te verduidelijken:
- Voorbeeld 1: 2/3 ÷ 1/2.
- Keer 1/2 om: 2/1.
- Vermenigvuldig: 2/3 x 2/1 = 4/3.
- Vereenvoudig: 4/3 = 1 1/3.
- Voorbeeld 2: 3/4 ÷ 2/5.
- Keer 2/5 om: 5/2.
- Vermenigvuldig: 3/4 x 5/2 = 15/8.
- Vereenvoudig: 15/8 = 1 7/8.
- Voorbeeld 3: 1/3 ÷ 3. (Herinner je dat 3 hetzelfde is als 3/1).
- Keer 3/1 om: 1/3.
- Vermenigvuldig: 1/3 x 1/3 = 1/9.
Delen van Gemengde Getallen
Het delen van gemengde getallen vereist een kleine extra stap. Voordat je de "keer om en vermenigvuldig" regel kunt toepassen, moet je eerst de gemengde getallen omzetten in onechte breuken.
Hoe zet je een gemengd getal om in een onechte breuk?
- Vermenigvuldig het gehele getal met de noemer.
- Tel de teller bij het resultaat op.
- Plaats dit nieuwe getal boven de oorspronkelijke noemer.
Bijvoorbeeld, om 2 1/4 om te zetten in een onechte breuk:
- 2 x 4 = 8.
- 8 + 1 = 9.
- De onechte breuk is 9/4.
Voorbeeld: 2 1/2 ÷ 1 1/3.
- Zet 2 1/2 om in een onechte breuk: 2 x 2 + 1 = 5. Dus 2 1/2 = 5/2.
- Zet 1 1/3 om in een onechte breuk: 1 x 3 + 1 = 4. Dus 1 1/3 = 4/3.
- Keer 4/3 om: 3/4.
- Vermenigvuldig: 5/2 x 3/4 = 15/8.
- Vereenvoudig: 15/8 = 1 7/8.
Tips en Trucs voor het Delen van Breuken
- Vereenvoudig vóór het vermenigvuldigen: Als er gemeenschappelijke factoren zijn in de tellers en noemers, vereenvoudig dan eerst. Dit maakt de berekeningen gemakkelijker.
- Gebruik visuele hulpmiddelen: Teken diagrammen of gebruik manipulatieven (bijvoorbeeld fraction blocks) om het concept visueel te maken. Dit kan vooral nuttig zijn voor beginners.
- Oefen, oefen, oefen: Hoe meer je oefent, hoe beter je wordt. Zoek online oefeningen of maak je eigen problemen.
- Controleer je antwoorden: Gebruik een rekenmachine of online breuk calculator om je antwoorden te controleren.
- Wees niet bang om fouten te maken: Fouten zijn leermogelijkheden. Analyseer je fouten en probeer te begrijpen waar het mis ging.
Veelgemaakte Fouten om te Vermijden
Er zijn een paar veelgemaakte fouten die je kunt vermijden:
- Vergeten de tweede breuk om te keren: Dit is de meest voorkomende fout. Herinner jezelf eraan dat je alleen de tweede breuk (de deler) omkeert.
- Tellers en noemers optellen in plaats van vermenigvuldigen: Onthoud dat je bij het vermenigvuldigen van breuken de tellers en noemers afzonderlijk vermenigvuldigt.
- Niet vereenvoudigen: Vergeet niet om je eindantwoord te vereenvoudigen.
- Vergeten gemengde getallen om te zetten in onechte breuken: Zorg ervoor dat je dit doet voordat je de "keer om en vermenigvuldig" regel toepast.
Breuken in het Echte Leven: Praktische Voorbeelden
Laten we eens kijken naar een paar concrete voorbeelden waarin het delen van breuken van pas komt:
- Bakken: Je hebt een recept nodig voor slechts 1/3 van een taart. Het originele recept vraagt om 3/4 kopje bloem. Hoeveel bloem heb je nodig? (3/4 ÷ 3 = 1/4 kopje).
- Houtbewerking: Je hebt een plank van 5 1/2 meter lang en je wilt er 4 gelijke stukken van maken. Hoe lang is elk stuk? (5 1/2 ÷ 4 = 11/2 ÷ 4 = 11/8 = 1 3/8 meter).
- Tijdmanagement: Je hebt 1/2 uur om 3 pagina's te lezen. Hoeveel tijd heb je per pagina? (1/2 ÷ 3 = 1/6 uur per pagina).
Door te oefenen met deze realistische scenario's, zul je het delen van breuken steeds beter begrijpen en toepassen.
Conclusie: Beheers het Delen van Breuken en Ontgrendel Nieuwe Mogelijkheden!
Het delen van breuken is een essentiële wiskundige vaardigheid die je op veel gebieden van je leven van pas kan komen. Door de eenvoudige regel "keer om en vermenigvuldig" te onthouden en veel te oefenen, kun je deze vaardigheid beheersen en met vertrouwen wiskundige problemen oplossen.
Dus, daag jezelf uit, oefen regelmatig en laat breuken geen struikelblok meer zijn, maar een springplank naar succes! Je hebt nu de tools en kennis om breuken te delen. Ga aan de slag en ontdek hoe je deze vaardigheid in je dagelijks leven kunt toepassen!


Bekijk ook deze gerelateerde berichten:
- Hoeveel Weken Is De Herfstvakantie
- Hoe Moet Je Bidden Islam Vrouwen
- Vanaf Welke Leeftijd Ben Je Leerplichtig
- Kand J.h. Van Der Velden Leeftijd
- Wat Is Sneller Dan Het Licht
- Hoe Lang Leeft Een Roodborstje
- Hoe Maak Je Een Katapult
- Economie Examen Havo 2022 Tijdvak 2
- Hoe Ziet Een Ct Scan Eruit
- Examen Wiskunde A Havo 2023
