Hoe Maak Je Een Formule Bij Een Grafiek

Heb je ooit naar een grafiek gekeken en gedacht: "Dit is interessant, maar ik zou willen dat ik de formule achter deze lijn of curve kon achterhalen?" Je bent niet de enige! Veel mensen vinden het lastig om de sprong van een visuele voorstelling naar een wiskundige formule te maken. Het lijkt misschien intimiderend, maar met de juiste aanpak en een beetje oefening is het zeker haalbaar. In dit artikel gaan we je stap voor stap uitleggen hoe je dat doet, zodat je grafieken niet alleen kunt lezen, maar ook kunt interpreteren en vertalen naar een bruikbare formule.

Waarom zou je een formule bij een grafiek willen maken?

Voordat we beginnen, is het belangrijk om te begrijpen waarom je dit zou willen doen. Er zijn diverse redenen:

Kortom, het omzetten van een grafiek naar een formule geeft je een krachtig instrument in handen om data te analyseren en te interpreteren.

De basis: Wat voor type grafiek heb je?

De eerste stap is het identificeren van het type grafiek. Dit is cruciaal, omdat de aanpak voor het bepalen van de formule afhangt van de vorm van de grafiek. Hier zijn enkele veelvoorkomende types:

Lineaire grafieken

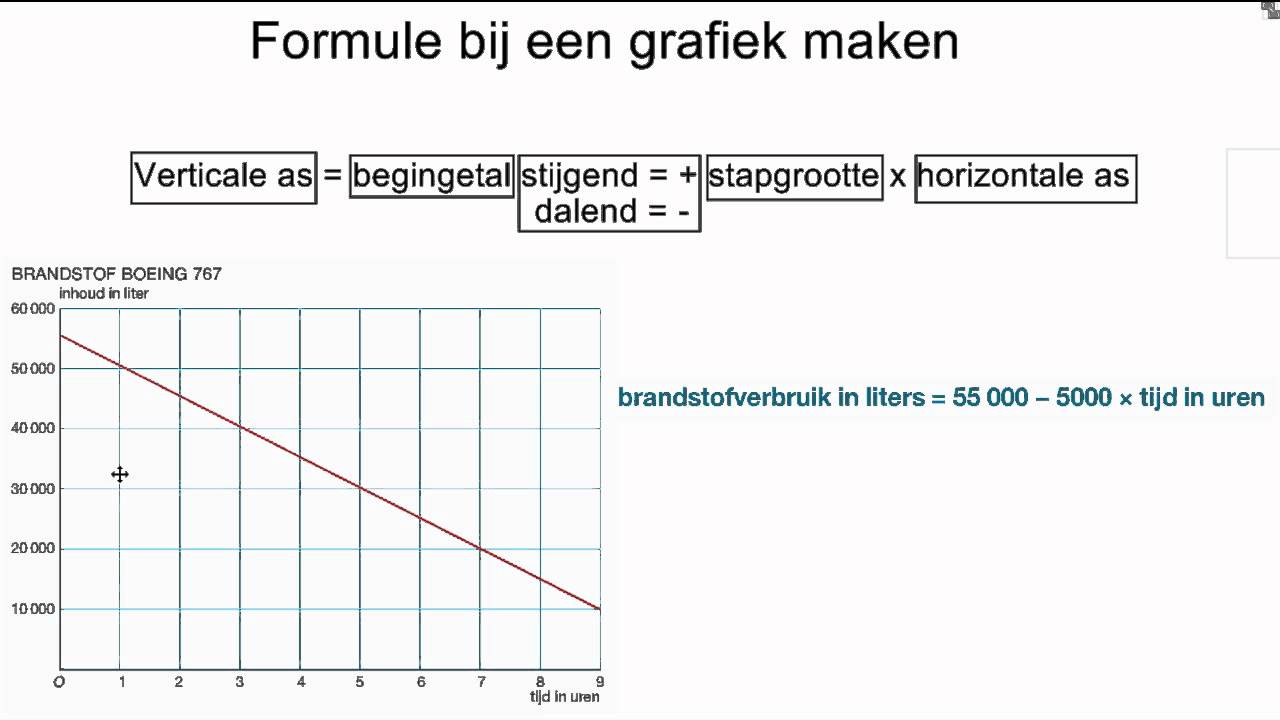
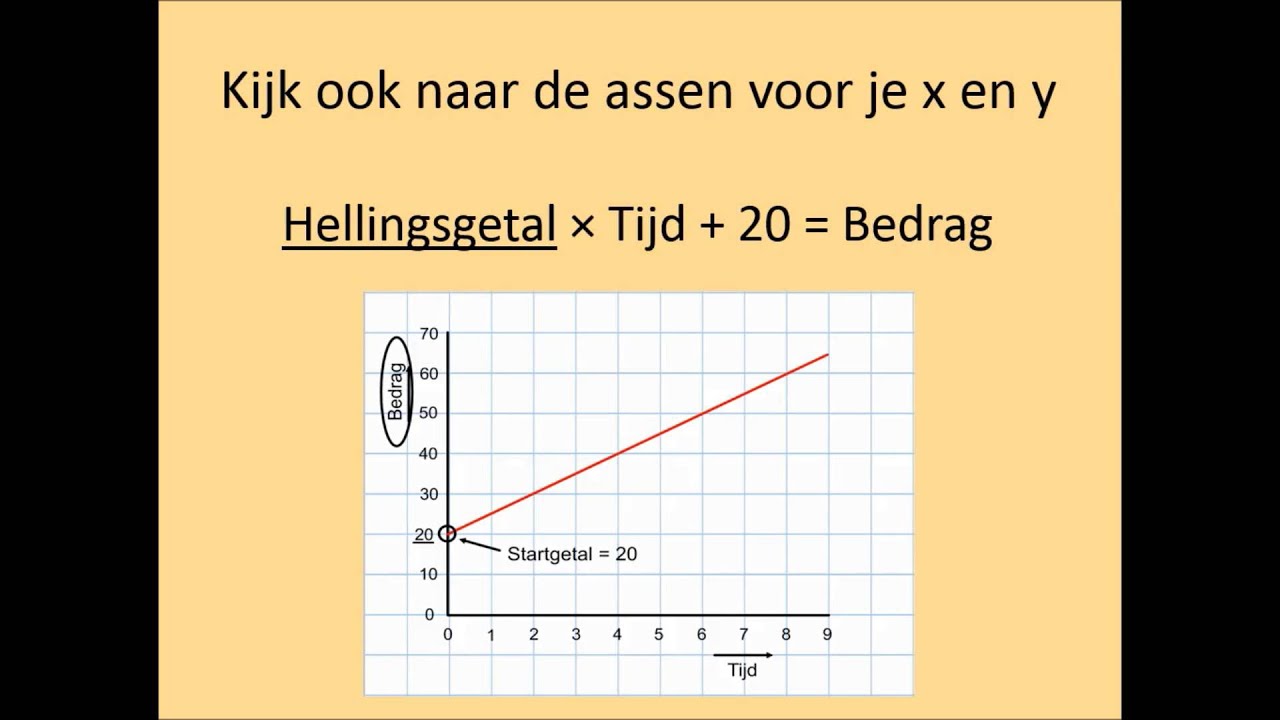
Lineaire grafieken zijn de eenvoudigste. Ze worden gekenmerkt door een rechte lijn. De algemene formule voor een lineaire grafiek is:

y = mx + b

Waar:

Om de formule te bepalen, moet je de helling (m) en de y-intercept (b) bepalen.

Kwadratische grafieken

Kwadratische grafieken hebben de vorm van een parabool (een U-vormige curve). De algemene formule is:

y = ax² + bx + c

Waar:

Het bepalen van de constanten a, b en c vereist meer stappen dan bij een lineaire grafiek. Je kunt bijvoorbeeld drie punten van de grafiek gebruiken om een stelsel van vergelijkingen op te lossen.

Exponentiële grafieken

Exponentiële grafieken laten een snelle toename of afname zien. De algemene formule is:

y = ab^x

Waar:

Exponentiële grafieken worden vaak gebruikt om groei of verval te modelleren, zoals de groei van een populatie of het verval van een radioactieve stof.

Andere grafiektypes

Er zijn natuurlijk nog veel meer soorten grafieken, zoals logaritmische grafieken, trigonometrische grafieken, en polynoomgrafieken van hogere graad. De aanpak voor het bepalen van de formule wordt steeds complexer naarmate de grafiek ingewikkelder wordt.

Stap-voor-stap: Hoe maak je een formule bij een grafiek

Laten we eens kijken naar de stappen die je kunt volgen om een formule te bepalen voor een grafiek.

1. Identificeer het type grafiek

Zoals eerder besproken, is dit de eerste en cruciale stap. Kijk goed naar de vorm van de grafiek en bepaal of het een rechte lijn, een parabool, een exponentiële curve, of iets anders is. Gebruik je wiskundige kennis om te helpen.

2. Kies relevante punten

Kies een aantal punten op de grafiek die je goed kunt aflezen. Voor een lineaire grafiek heb je minimaal twee punten nodig. Voor een kwadratische grafiek heb je minimaal drie punten nodig. Hoe nauwkeuriger je de punten kunt aflezen, hoe nauwkeuriger de formule zal zijn. Probeer duidelijke punten te kiezen, zoals snijpunten met de assen.

3. Stel vergelijkingen op

Gebruik de algemene formule van het grafiektype en de gekozen punten om vergelijkingen op te stellen. Vervang de x- en y-waarden van de punten in de algemene formule. Dit geeft je een stelsel van vergelijkingen met de onbekende constanten (bijvoorbeeld m en b voor een lineaire grafiek, of a, b en c voor een kwadratische grafiek).

4. Los de vergelijkingen op

Los het stelsel van vergelijkingen op om de waarden van de onbekende constanten te bepalen. Er zijn verschillende manieren om dit te doen, zoals substitutie, eliminatie, of matrixrekening. Gebruik de wiskunde tools die je tot je beschikking hebt.

5. Controleer de formule

Nadat je de formule hebt bepaald, is het belangrijk om deze te controleren. Kies een aantal andere punten op de grafiek en kijk of de formule correcte y-waarden oplevert voor die x-waarden. Als de formule niet goed past bij de grafiek, heb je mogelijk een fout gemaakt in de berekeningen of heb je het verkeerde type grafiek geïdentificeerd.

Voorbeeld: Een lineaire grafiek

Laten we een voorbeeld bekijken van een lineaire grafiek. Stel dat we een grafiek hebben die door de punten (1, 3) en (3, 7) gaat.

1. Type grafiek: Het is een rechte lijn, dus het is een lineaire grafiek.
2. Algemene formule: y = mx + b
3. Vergelijkingen opstellen:
   • 3 = m(1) + b
   • 7 = m(3) + b
4. Vergelijkingen oplossen: We kunnen de eerste vergelijking aftrekken van de tweede vergelijking:
   • 4 = 2m
   • m = 2
   Vervang m = 2 in de eerste vergelijking:
   • 3 = 2(1) + b
   • b = 1
5. Formule: y = 2x + 1
6. Controle: Laten we het punt (2, 5) controleren. Als we x = 2 invullen in de formule, krijgen we y = 2(2) + 1 = 5. Dit klopt, dus de formule is waarschijnlijk correct.

Tips en trucs

Het bepalen van de formule bij een grafiek is een waardevolle vaardigheid die je kunt gebruiken in veel verschillende contexten. Met de juiste aanpak en een beetje oefening, kun je leren om grafieken niet alleen te lezen, maar ook te interpreteren en te vertalen naar een bruikbare formule.