Hoeken Van Een Driehoek Berekenen

Heb je je ooit afgevraagd hoe je de hoeken van een driehoek kunt berekenen, zelfs als je niet alle informatie hebt? Misschien ben je een student die worstelt met geometrie, een doe-het-zelver die een nauwkeurig schuin dak wil bouwen, of gewoon iemand die nieuwsgierig is naar de wiskunde achter alledaagse vormen. Wat je reden ook is, dit artikel is geschreven voor jou. We gaan samen op ontdekkingstocht door de wereld van driehoeken en hun hoeken.

Waarom is het Belangrijk om Hoekenen van een Driehoek te Berekenen?

Het berekenen van hoeken van een driehoek is meer dan alleen een schoolse activiteit. Het is een fundamentele vaardigheid met toepassingen in diverse gebieden, waaronder:

• Architectuur en constructie: Voor het ontwerpen van stabiele en esthetisch aantrekkelijke gebouwen. Denk aan de hoek van een dak, de helling van een trap, of de verbindingen tussen verschillende constructie-elementen.
• Navigatie: Bij het bepalen van koersen en afstanden, zowel op zee als in de lucht. Denk hierbij aan het gebruik van triangulatie, waarbij de positie wordt bepaald aan de hand van hoeken ten opzichte van bekende punten.
• Engineering: Voor het ontwerpen van machines en bruggen. Een juiste hoekberekening is cruciaal voor de functionaliteit en veiligheid van dergelijke constructies.
• Game ontwikkeling: Voor het creëren van realistische bewegingen en perspectieven. De hoeken van objecten bepalen hoe ze op het scherm worden weergegeven.
• Houtbewerking: Om nauwkeurige sneden te maken en perfect passende stukken te creëren.

Kortom, het begrijpen en kunnen berekenen van hoeken in een driehoek is een waardevolle skill die je in verschillende situaties van pas kan komen.

De Basisprincipes: Wat Je Moet Weten

Voordat we in de daadwerkelijke berekeningen duiken, zijn er een paar basisprincipes die we moeten begrijpen:

De Som van de Hoeken in een Driehoek

Dit is een fundamentele regel: De som van de hoeken in elke driehoek is altijd 180 graden. Dit geldt voor alle soorten driehoeken: gelijkzijdige, gelijkbenige, rechthoekige, stomphoekige en scherphoekige. Wiskundig gezien: ∠A + ∠B + ∠C = 180°.

Soorten Driehoeken

Het type driehoek dat we hebben, beïnvloedt de methoden die we kunnen gebruiken om de hoeken te berekenen. Hier zijn de belangrijkste types:

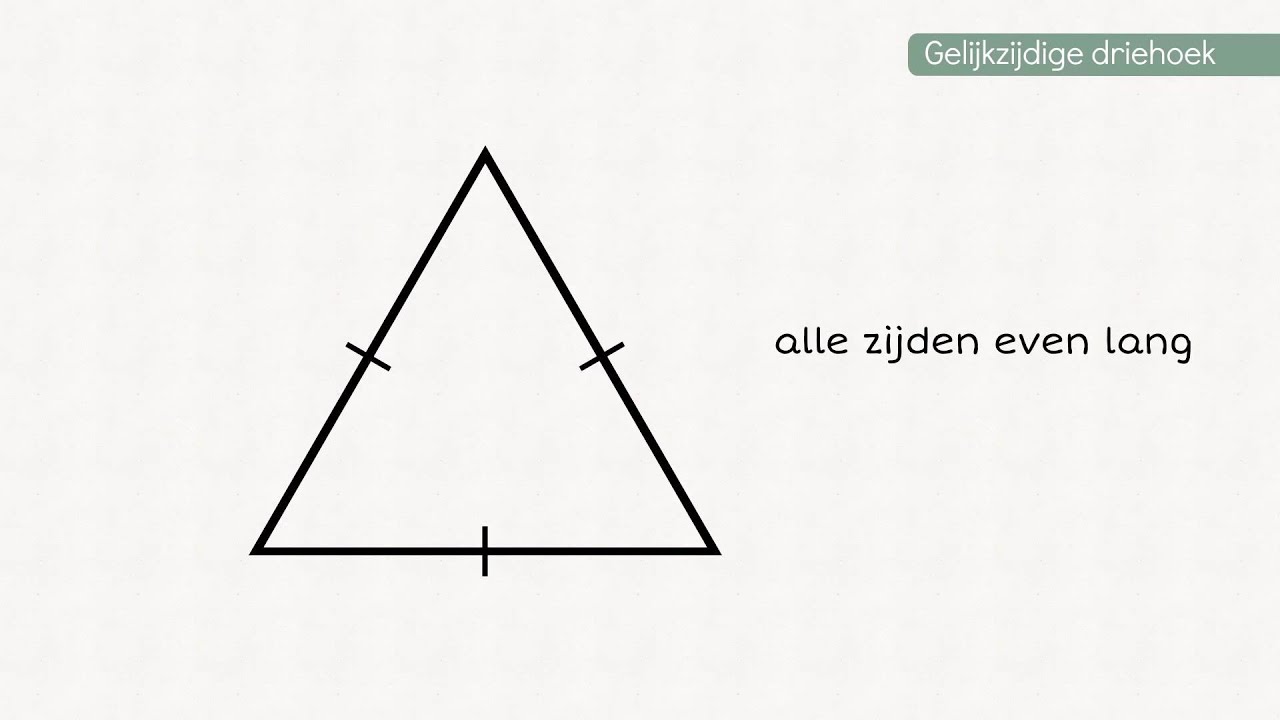
• Gelijkzijdige driehoek: Alle drie zijden zijn gelijk en alle drie hoeken zijn gelijk aan 60 graden.
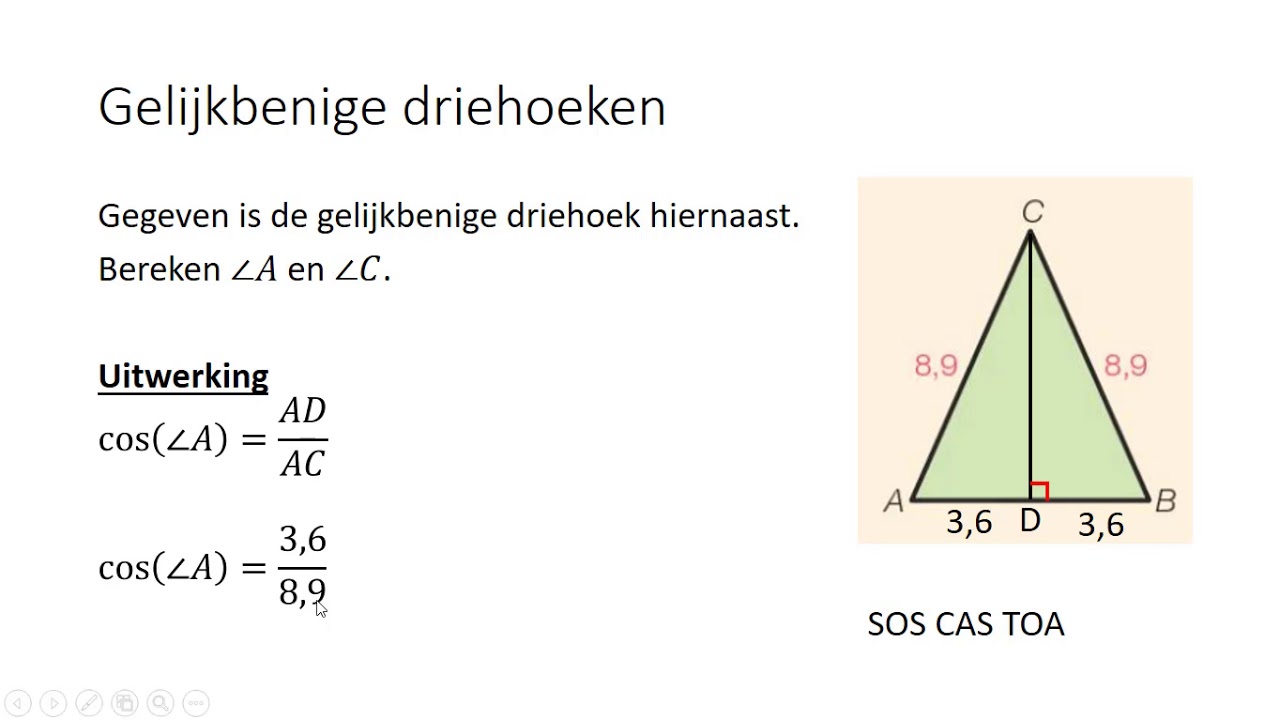
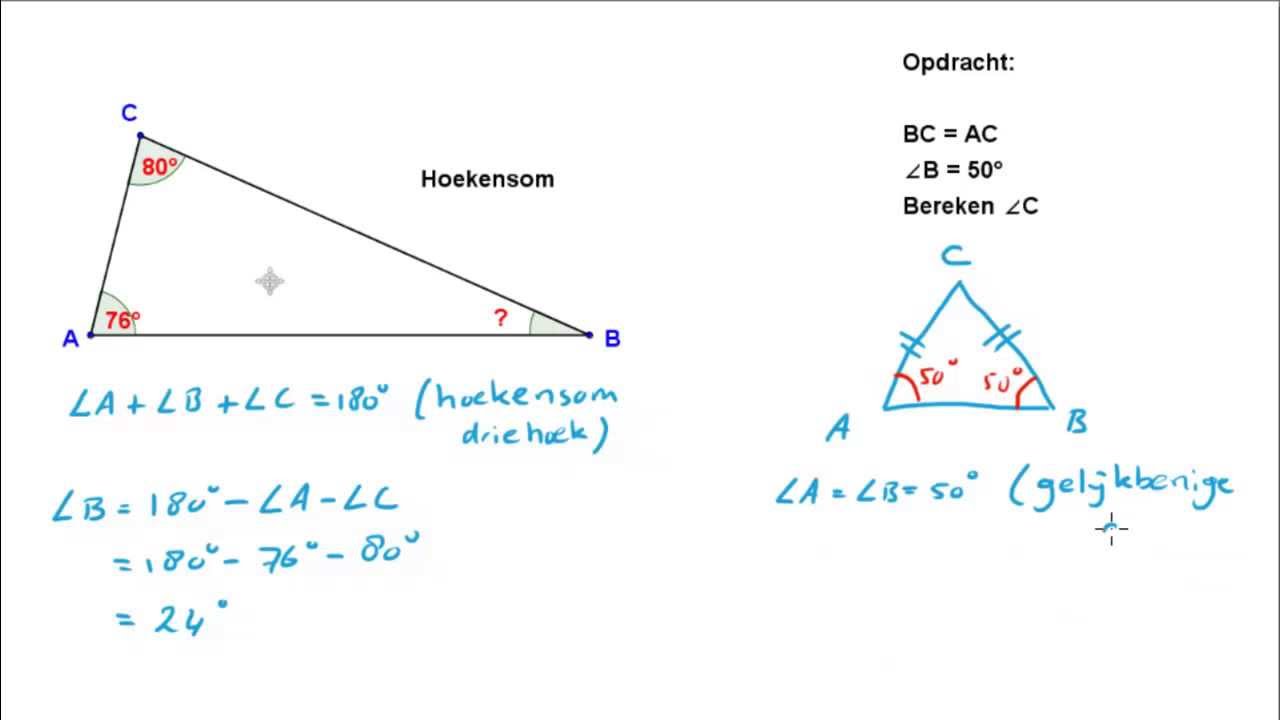
• Gelijkbenige driehoek: Twee zijden zijn gelijk en de hoeken tegenover die zijden zijn ook gelijk.
• Rechthoekige driehoek: Een van de hoeken is een rechte hoek (90 graden). De zijde tegenover de rechte hoek wordt de hypotenusa genoemd.
• Stomphoekige driehoek: Een van de hoeken is een stompe hoek (groter dan 90 graden).
• Scherphoekige driehoek: Alle drie hoeken zijn scherpe hoeken (kleiner dan 90 graden).

Trigonometrische Functies

Voor rechthoekige driehoeken kunnen we trigonometrische functies gebruiken: sinus (sin), cosinus (cos) en tangens (tan). Deze functies relateren de hoeken van een rechthoekige driehoek aan de verhoudingen van de lengtes van de zijden. De definities zijn als volgt:

• sin(hoek) = Overstaande zijde / Hypotenusa
• cos(hoek) = Aanliggende zijde / Hypotenusa
• tan(hoek) = Overstaande zijde / Aanliggende zijde

Hierbij is de "Overstaande zijde" de zijde tegenover de hoek die we bekijken, en de "Aanliggende zijde" is de zijde die aan de hoek grenst (maar niet de hypotenusa).

Methoden voor het Berekenen van Hoeken

Nu we de basisprincipes begrijpen, kunnen we kijken naar verschillende methoden om de hoeken van een driehoek te berekenen:

Methode 1: Bekende Hoeken Gebruiken

Als je twee hoeken van een driehoek weet, kun je de derde hoek eenvoudig berekenen door ze van 180 graden af te trekken:

∠C = 180° - ∠A - ∠B

Voorbeeld: Stel ∠A = 60° en ∠B = 80°. Dan is ∠C = 180° - 60° - 80° = 40°.

Methode 2: Trigonometrie in Rechthoekige Driehoeken

Als je een rechthoekige driehoek hebt en de lengte van twee zijden kent, kun je de trigonometrische functies gebruiken om de hoeken te berekenen:

1. Identificeer de bekende zijden (overstaand, aanliggend, hypotenusa) ten opzichte van de hoek die je wilt berekenen.
2. Kies de juiste trigonometrische functie:
   • Als je de overstaande zijde en de hypotenusa kent, gebruik je sinus (sin).
   • Als je de aanliggende zijde en de hypotenusa kent, gebruik je cosinus (cos).
   • Als je de overstaande zijde en de aanliggende zijde kent, gebruik je tangens (tan).
3. Bereken de hoek met behulp van de inverse trigonometrische functie (arcsin, arccos, arctan) op je rekenmachine. Deze functies worden vaak aangeduid als sin^-1, cos^-1 en tan^-1.

Voorbeeld: In een rechthoekige driehoek is de overstaande zijde 5 cm en de hypotenusa 10 cm. Om de hoek tegenover de overstaande zijde te berekenen, gebruik je sin(hoek) = 5/10 = 0.5. De inverse sinus van 0.5 is 30°, dus de hoek is 30 graden.

Methode 3: De Sinusregel

De Sinusregel is handig als je de lengte van één zijde en de overstaande hoek kent, plus de lengte van een andere zijde (of de overstaande hoek daarvan). De regel stelt:

a / sin(A) = b / sin(B) = c / sin(C)

Waar a, b, en c de lengtes van de zijden zijn, en A, B, en C de hoeken tegenover die zijden.

Voorbeeld: Stel a = 10 cm, A = 30°, en b = 15 cm. We willen hoek B berekenen. Dan hebben we:

10 / sin(30°) = 15 / sin(B)

sin(B) = (15 * sin(30°)) / 10 = (15 * 0.5) / 10 = 0.75

B = arcsin(0.75) ≈ 48.59°

Je kunt nu de derde hoek (C) berekenen met de regel dat de hoeken samen 180° zijn.

Methode 4: De Cosinusregel

De Cosinusregel is bruikbaar in twee situaties:

• Wanneer je alle drie de zijden kent en je wilt een van de hoeken berekenen.
• Wanneer je twee zijden en de ingesloten hoek (de hoek tussen die twee zijden) kent en je wilt de derde zijde berekenen (hoewel dit artikel zich richt op het berekenen van hoeken, is het goed om te weten dat de Cosinusregel ook voor zijden kan worden gebruikt).

De Cosinusregel luidt als volgt:

a² = b² + c² - 2bc * cos(A)

b² = a² + c² - 2ac * cos(B)

c² = a² + b² - 2ab * cos(C)

Waar a, b, en c de lengtes van de zijden zijn, en A, B, en C de hoeken tegenover die zijden.

Voorbeeld: Stel a = 8 cm, b = 5 cm, en c = 7 cm. We willen hoek A berekenen. Dan gebruiken we de eerste vergelijking:

8² = 5² + 7² - 2 * 5 * 7 * cos(A)

64 = 25 + 49 - 70 * cos(A)

70 * cos(A) = 25 + 49 - 64 = 10

cos(A) = 10 / 70 ≈ 0.1429

A = arccos(0.1429) ≈ 81.79°

Tips en Trucs voor Nauwkeurige Berekeningen

• Gebruik een rekenmachine met trigonometrische functies en inverse trigonometrische functies.
• Controleer je antwoord. Zorg ervoor dat de som van de hoeken in de driehoek 180 graden is.
• Wees nauwkeurig. Gebruik voldoende decimalen in je berekeningen om afrondingsfouten te minimaliseren.
• Oefen! Hoe meer je oefent, hoe beter je wordt in het herkennen van de juiste methode en het uitvoeren van de berekeningen.

Tot Slot: De Waarde van Kennis

Het berekenen van de hoeken van een driehoek is een vaardigheid die je niet alleen in de schoolbanken, maar ook in de echte wereld van pas kan komen. Of je nu een probleem in een wiskundeles wilt oplossen, een doe-het-zelf project wilt uitvoeren, of gewoon je ruimtelijk inzicht wilt verbeteren, de kennis die je hier hebt opgedaan, zal van onschatbare waarde zijn. Blijf leren en ontdekken, want de wereld van de wiskunde zit vol met fascinerende concepten die wachten om ontdekt te worden.