Hoeveel Diagonalen Heeft Een Twintighoek

Het bepalen van het aantal diagonalen in een veelhoek, met name een twintighoek (een polygoon met 20 zijden), is een interessant geometrisch probleem. In dit artikel zullen we dieper ingaan op de formule om dit aantal te berekenen, deze formule uitleggen en illustreren met voorbeelden. We zullen ook kort ingaan op de relevantie van dit concept in verschillende vakgebieden.

Wat is een Diagonaal?

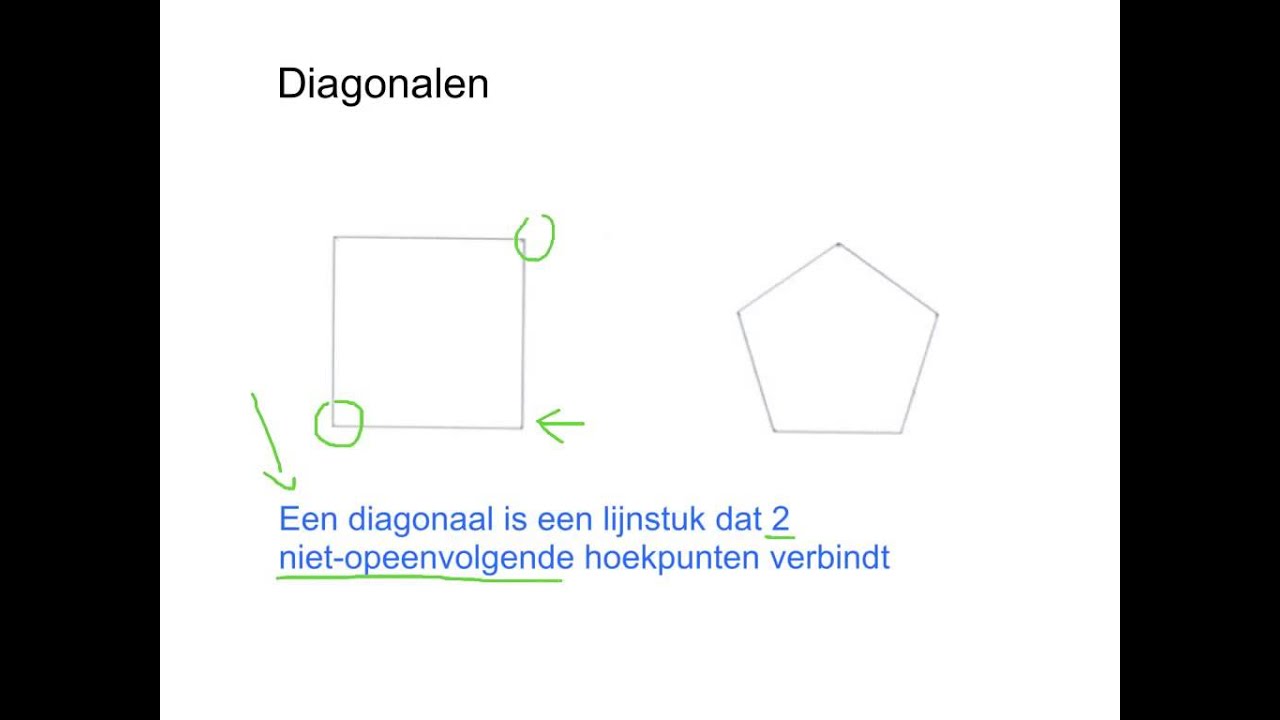
Voordat we ons op de twintighoek richten, is het belangrijk om te definiëren wat een diagonaal precies is. Een diagonaal is een lijnsegment dat twee niet-opeenvolgende hoekpunten van een veelhoek verbindt. Met andere woorden, het is een lijn die geen zijde van de veelhoek is.

Stel je een vierkant voor. Het heeft vier hoekpunten. De zijden verbinden opeenvolgende hoekpunten. De diagonalen verbinden de hoekpunten die niet direct naast elkaar liggen. Een vierkant heeft dus twee diagonalen.

De Formule voor het Berekenen van Diagonalen

Er is een algemene formule om het aantal diagonalen in een willekeurige veelhoek te berekenen, ongeacht het aantal zijden. Deze formule is:

n(n - 3) / 2

Waarbij 'n' het aantal zijden (of hoekpunten) van de veelhoek voorstelt. Laten we eens kijken waar deze formule vandaan komt.

Uitleg van de Formule

Elk hoekpunt in een veelhoek kan verbonden worden met alle andere hoekpunten, behalve met zichzelf en de twee aangrenzende hoekpunten (want die verbindingen vormen zijden). Dus, vanuit één hoekpunt kunnen we (n - 3) diagonalen trekken.

Aangezien er 'n' hoekpunten zijn, lijkt het alsof we n(n - 3) diagonalen hebben. Echter, we tellen elke diagonaal twee keer (één keer vanuit elk van de twee eindpunten van de diagonaal). Daarom moeten we de totale telling delen door 2 om het juiste aantal diagonalen te krijgen. Dit leidt tot de formule: n(n - 3) / 2.

Het Aantal Diagonalen in een Twintighoek

Nu kunnen we de formule toepassen om het aantal diagonalen in een twintighoek te berekenen. Een twintighoek heeft 20 zijden, dus n = 20.

Aantal diagonalen = 20(20 - 3) / 2

Aantal diagonalen = 20(17) / 2

Aantal diagonalen = 340 / 2

Aantal diagonalen = 170

Dus, een twintighoek heeft 170 diagonalen.

Voorbeelden en Toepassingen

Hoewel het tellen van diagonalen misschien een puur theoretische oefening lijkt, heeft het wel degelijk toepassingen in verschillende gebieden.

Grafentheorie

In de grafentheorie wordt een veelhoek vaak gemodelleerd als een complete graaf. Het aantal diagonalen komt overeen met het aantal mogelijke verbindingen tussen knooppunten, minus de verbindingen die al als zijden van de graaf gedefinieerd zijn. Dit is belangrijk voor het optimaliseren van netwerkverbindingen en het analyseren van relaties tussen objecten.

Architectuur en Design

Diagonalen worden gebruikt in architectuur en design om stabiliteit en sterkte aan constructies te geven. Denk bijvoorbeeld aan de steunbalken in een brug of een dakconstructie. Hoewel een twintighoek zelden direct in een gebouw wordt gebruikt, kunnen de principes van diagonale versterking worden toegepast op meer complexe geometrische vormen die wel in architectuur voorkomen.

Computer Graphics

In computer graphics worden veelhoeken gebruikt om 3D-objecten te modelleren. Het berekenen van diagonalen is essentieel voor het trianguleren van veelhoeken. Triangulatie is het proces waarbij een veelhoek wordt opgedeeld in driehoeken. Dit is nodig omdat driehoeken de meest stabiele en makkelijkst te renderen polygonen zijn. Het aantal diagonalen bepaalt het aantal manieren waarop een veelhoek kan worden getrianguleerd.

Verschillende Veelhoeken en Hun Diagonalen

Laten we eens kijken naar het aantal diagonalen van enkele andere veelhoeken:

• Driehoek (3 zijden): 3(3-3)/2 = 0 diagonalen
• Vierhoek (4 zijden): 4(4-3)/2 = 2 diagonalen
• Vijfhoek (5 zijden): 5(5-3)/2 = 5 diagonalen
• Zeshoek (6 zijden): 6(6-3)/2 = 9 diagonalen
• Achtkhoek (8 zijden): 8(8-3)/2 = 20 diagonalen
• Tienhoek (10 zijden): 10(10-3)/2 = 35 diagonalen

Je kunt zien dat het aantal diagonalen snel toeneemt naarmate het aantal zijden toeneemt.

Complexiteit en Algoritmen

Het berekenen van het aantal diagonalen met de formule n(n-3)/2 is zeer efficiënt. De complexiteit is O(1), wat betekent dat de berekening in constante tijd kan worden uitgevoerd, ongeacht de grootte van 'n'. Er zijn geen complexe algoritmen nodig. Echter, het probleem van het vinden van *alle* diagonalen, bijvoorbeeld in een computerprogramma, vereist een iets ander algoritme met een hogere complexiteit, namelijk O(n^2), omdat je alle mogelijke paren van niet-opeenvolgende hoekpunten moet bekijken.

Overwegingen bij het Programmeren

Als je een programma schrijft om de diagonalen van een veelhoek te vinden, moet je rekening houden met de manier waarop de veelhoek wordt voorgesteld. Meestal worden de hoekpunten opgeslagen als een lijst van coördinaten. Het algoritme moet dan door de lijst itereren en controleren welke hoekpunten niet-opeenvolgend zijn.

Conclusie

Het aantal diagonalen in een twintighoek is 170. Dit aantal werd berekend met de formule n(n - 3) / 2, die een algemene regel biedt voor het bepalen van het aantal diagonalen in elke veelhoek. Hoewel het tellen van diagonalen misschien een abstract concept lijkt, heeft het praktische toepassingen in de grafentheorie, architectuur, design en computer graphics. Het begrijpen van de wiskundige principes achter geometrische vormen stelt ons in staat om de wereld om ons heen beter te begrijpen en te modelleren.

Dus, de volgende keer dat je een veelhoek ziet, daag jezelf dan uit om te visualiseren hoeveel diagonalen erin verborgen zitten! Denk erover na hoe deze diagonalen de structuur versterken of hoe ze in een digitaal model zouden worden weergegeven. Blijf nieuwsgierig en blijf leren!