Hoeveel Diagonalen Heeft Een Veelhoek

Het bepalen van het aantal diagonalen in een veelhoek is een fundamenteel concept in de meetkunde. Veelhoeken komen in talloze vormen en maten voor, van eenvoudige driehoeken tot complexe figuren met vele zijden. Het begrijpen hoe je het aantal diagonalen berekent, is niet alleen een academische oefening, maar ook een nuttige vaardigheid met toepassingen in diverse gebieden. In dit artikel duiken we dieper in de materie en ontrafelen we de formule achter deze berekening, illustreren we het met voorbeelden en bespreken we enkele praktische toepassingen.

Wat is een Diagonaal?

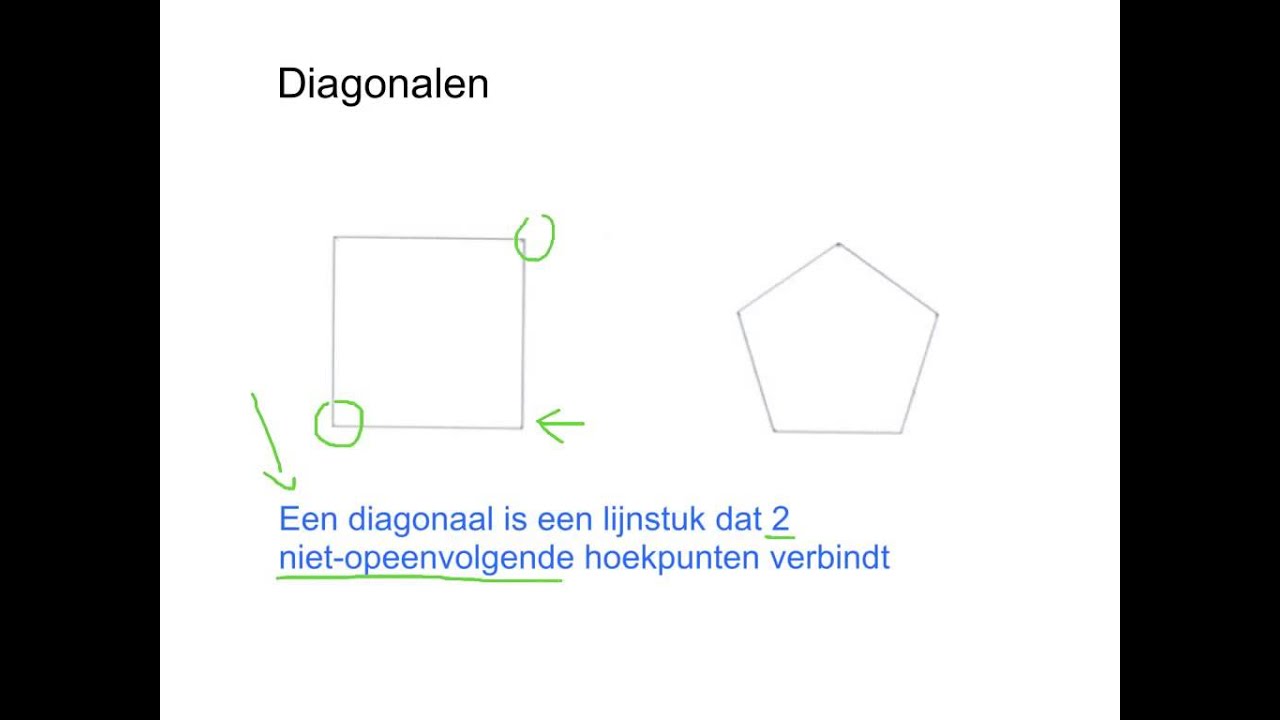
Voordat we het aantal diagonalen kunnen berekenen, is het essentieel om te definiëren wat een diagonaal precies is. Een diagonaal is een lijnsegment dat twee niet-opeenvolgende hoekpunten van een veelhoek verbindt. Met andere woorden, het is een lijnstuk dat geen zijde van de veelhoek is.

Denk bijvoorbeeld aan een vierkant. Het heeft vier hoekpunten en vier zijden. De diagonalen zijn de lijnen die de tegenoverliggende hoekpunten verbinden. Een driehoek daarentegen heeft geen diagonalen, omdat alle hoekpunten opeenvolgend zijn verbonden.

De Formule voor het Aantal Diagonalen

Er is een elegante formule om het aantal diagonalen in een veelhoek te berekenen, afhankelijk van het aantal zijden. De formule is als volgt:

Aantal diagonalen = n(n - 3) / 2

Waarbij 'n' staat voor het aantal zijden (of hoekpunten) van de veelhoek. Laten we de componenten van deze formule eens nader bekijken:

Uitleg van de Formule

• n(n - 3): Elk hoekpunt kan worden verbonden met (n - 3) andere hoekpunten om een diagonaal te vormen. We trekken er 3 af omdat:
  • Het hoekpunt zelf niet mee kan worden verbonden.
  • De twee aangrenzende hoekpunten (de hoekpunten aan weerszijden) al via zijden verbonden zijn.
• / 2: We delen het resultaat door 2 omdat elke diagonaal twee keer wordt geteld. Als we elk hoekpunt bekijken en lijnen tekenen, tellen we de diagonaal van hoekpunt A naar hoekpunt C, en vervolgens de diagonaal van hoekpunt C naar hoekpunt A. Dit is dezelfde diagonaal, dus we moeten de dubbele telling corrigeren door te delen door 2.

Voorbeelden van het Gebruik van de Formule

Laten we de formule toepassen op verschillende veelhoeken om het aantal diagonalen te bepalen:

Vierkant (n = 4)

Aantal diagonalen = 4(4 - 3) / 2 = 4(1) / 2 = 2

Een vierkant heeft inderdaad 2 diagonalen.

Vijfhoek (n = 5)

Aantal diagonalen = 5(5 - 3) / 2 = 5(2) / 2 = 5

Een vijfhoek heeft 5 diagonalen.

Zeshoek (n = 6)

Aantal diagonalen = 6(6 - 3) / 2 = 6(3) / 2 = 9

Een zeshoek heeft 9 diagonalen.

Zevenhoek (n = 7)

Aantal diagonalen = 7(7 - 3) / 2 = 7(4) / 2 = 14

Een zevenhoek heeft 14 diagonalen.

Achthoek (n = 8)

Aantal diagonalen = 8(8 - 3) / 2 = 8(5) / 2 = 20

Een achthoek heeft 20 diagonalen.

Zoals je kunt zien, neemt het aantal diagonalen snel toe naarmate het aantal zijden van de veelhoek toeneemt. Dit komt door de kwadratische relatie tussen het aantal zijden en het aantal diagonalen in de formule.

Praktische Toepassingen van het Berekenen van Diagonalen

Hoewel het berekenen van diagonalen misschien een abstract wiskundig concept lijkt, heeft het wel degelijk praktische toepassingen in diverse velden:

• Bouwkunde en Engineering: Bij het ontwerpen van structuren zoals bruggen en gebouwen is het belangrijk om de sterkte en stabiliteit te waarborgen. Diagonalen worden vaak gebruikt om structuren te verstevigen en te voorkomen dat ze vervormen onder belasting. Het begrijpen van de relatie tussen het aantal zijden en diagonalen kan ingenieurs helpen bij het optimaliseren van het ontwerp.
• Computergraphics: In de computergraphics worden veelhoeken gebruikt om objecten weer te geven. Bij het renderen van deze objecten is het soms nodig om de veelhoeken op te delen in kleinere stukken, bijvoorbeeld in driehoeken (triangulatie). Het aantal diagonalen kan van pas komen bij het bepalen van de optimale manier om een veelhoek te trianguleren.
• Netwerkanalyse: In de netwerkanalyse kunnen veelhoeken worden gebruikt om de connectiviteit van een netwerk weer te geven. De diagonalen kunnen dan de verbindingen tussen niet-aangrenzende knooppunten in het netwerk voorstellen. Het tellen van diagonalen kan een maatstaf zijn voor de complexiteit en redundantie van het netwerk.
• Geometrisch Ontwerp: Bij het ontwerpen van patronen en tessellaties is het begrijpen van de eigenschappen van veelhoeken, waaronder het aantal diagonalen, cruciaal. Het kan helpen bij het creëren van visueel aantrekkelijke en wiskundig consistente ontwerpen.

Complexere Voorbeelden en Uitzonderingen

De formule n(n - 3) / 2 is van toepassing op convexe veelhoeken. Een convexe veelhoek is een veelhoek waarbij alle inwendige hoeken kleiner zijn dan 180 graden. Met andere woorden, als je een lijnsegment tussen twee willekeurige punten binnen de veelhoek tekent, ligt dat lijnsegment volledig binnen de veelhoek.

Bij concave veelhoeken (ook wel niet-convexe veelhoeken genoemd), waarin minstens één inwendige hoek groter is dan 180 graden, kan de formule nog steeds worden gebruikt, maar de interpretatie van de diagonalen kan complexer worden. Sommige diagonalen kunnen buiten de veelhoek vallen.

Voor zeer complexe veelhoeken, vooral die met veel zijden, kan het visueel tellen van diagonalen een tijdrovende en foutgevoelige taak zijn. De formule biedt dan een snelle en betrouwbare manier om het aantal diagonalen te bepalen.

Conclusie

Het berekenen van het aantal diagonalen in een veelhoek is een eenvoudig maar krachtig concept in de meetkunde. De formule n(n - 3) / 2 biedt een handige manier om het aantal diagonalen te bepalen, ongeacht het aantal zijden. Of je nu een student bent die meetkunde studeert, een ingenieur die structuren ontwerpt, of een ontwerper die patronen creëert, het begrijpen van deze formule kan van grote waarde zijn.

Dus, de volgende keer dat je een veelhoek tegenkomt, daag jezelf dan uit om het aantal diagonalen te berekenen. Het is een leuke en leerzame oefening die je wiskundige vaardigheden zal verbeteren en je waardering voor de schoonheid van de meetkunde zal vergroten!