Hoeveel Diagonalen Heeft Een Zeshoek

Heb je je ooit afgevraagd hoeveel diagonalen een zeshoek eigenlijk heeft? Het is een vraag die misschien eenvoudig lijkt, maar die een interessante reis door de wereld van de meetkunde onthult. Dit artikel is bedoeld voor iedereen die nieuwsgierig is naar wiskunde, van leerlingen tot hobbyisten. We gaan samen ontdekken hoe je het aantal diagonalen in een zeshoek kunt berekenen en de logica erachter begrijpen. Geen ingewikkelde wiskundige formules zonder uitleg; we gaan het stap voor stap bekijken.

Wat is een Diagonaal Eigenlijk?

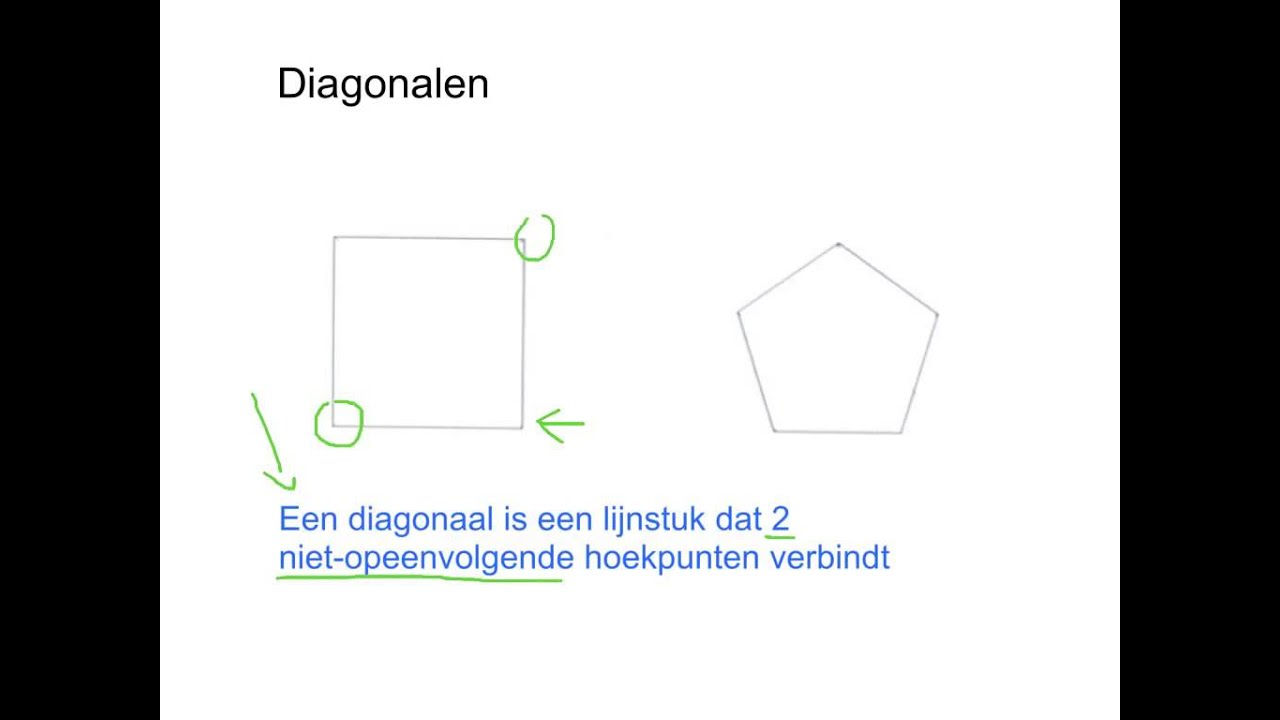
Voordat we in de zeshoek duiken, moeten we even stilstaan bij wat een diagonaal precies is. In de meetkunde is een diagonaal een lijnstuk dat twee niet-opeenvolgende hoekpunten van een veelhoek verbindt. Met andere woorden, het is een lijn die je kunt tekenen binnen een figuur, van de ene hoek naar een andere, zonder dat het een van de zijden van de figuur is. Stel je voor dat je een doos hebt. Een diagonaal zou een lijn zijn die van de ene hoek bovenop naar de tegenoverliggende hoek aan de onderkant loopt.

Het is cruciaal om het verschil tussen een zijde en een diagonaal te begrijpen. De zijden vormen de buitenrand van de veelhoek, terwijl diagonalen 'binnenin' de figuur lopen.

De Zeshoek: Een Kennismaking

Nu we weten wat een diagonaal is, laten we eens kijken naar onze ster van de show: de zeshoek. Een zeshoek is een veelhoek met zes zijden en zes hoekpunten. Het is een figuur die je overal om je heen kunt vinden, van de cellen in een honingraat tot bepaalde moeren en bouten. Er bestaan regelmatige en onregelmatige zeshoeken. Een regelmatige zeshoek heeft zes gelijke zijden en zes gelijke hoeken. Een onregelmatige zeshoek heeft zijden en/of hoeken van verschillende groottes.

Voor de berekening van het aantal diagonalen maakt het in principe niet uit of de zeshoek regelmatig of onregelmatig is. Het enige wat telt, is het aantal hoekpunten.

Het Aantal Diagonalen: Een Intuïtieve Aanpak

Laten we beginnen met een intuïtieve aanpak. We kunnen de zeshoek tekenen en proberen alle diagonalen te tekenen. Dit is een goede manier om te beginnen, maar het kan snel ingewikkeld worden en het risico op fouten neemt toe. Maar het geeft wel een visuele representatie.

Stel je voor dat je de zes hoekpunten van de zeshoek hebt. Vanuit elk hoekpunt kun je lijnen trekken naar de andere hoekpunten. Maar pas op! We moeten de volgende dingen in gedachten houden:

• Je kunt geen lijn trekken van een hoekpunt naar zichzelf.
• Je kunt geen lijn trekken naar de twee aangrenzende hoekpunten (omdat dat zijden zijn, geen diagonalen).

Dus, vanuit elk hoekpunt van de zeshoek kun je lijnen trekken naar 6 - 1 - 2 = 3 andere hoekpunten. Dat betekent dat je 3 diagonalen kunt tekenen vanuit elk hoekpunt.

Aangezien er 6 hoekpunten zijn, zou je kunnen denken dat er 6 * 3 = 18 diagonalen zijn. Maar wees voorzichtig! We hebben elke diagonaal dubbel geteld. De diagonaal van hoekpunt A naar hoekpunt C is dezelfde diagonaal als van hoekpunt C naar hoekpunt A. Daarom moeten we het resultaat delen door 2.

Dus, het aantal diagonalen is (6 * 3) / 2 = 9. Een zeshoek heeft dus 9 diagonalen.

De Formule: Een Meer Algemene Methode

De intuïtieve aanpak is handig voor de zeshoek, maar wat als we een veelhoek hebben met veel meer zijden? Dan wordt het tekenen en tellen van diagonalen erg lastig. Gelukkig is er een formule die we kunnen gebruiken om het aantal diagonalen in een veelhoek met 'n' zijden te berekenen:

Aantal diagonalen = n * (n - 3) / 2

Waar 'n' het aantal zijden (en hoekpunten) van de veelhoek is.

Laten we deze formule toepassen op de zeshoek. In dit geval is n = 6:

Aantal diagonalen = 6 * (6 - 3) / 2 = 6 * 3 / 2 = 18 / 2 = 9

We komen dus weer op hetzelfde antwoord uit: 9 diagonalen.

Waarom werkt deze formule?

Laten we de formule eens ontleden om te begrijpen waarom deze werkt:

• n * (n - 3): Dit berekent het aantal lijnen dat je vanuit elk hoekpunt kunt trekken, waarbij je jezelf en de twee aangrenzende hoekpunten uitsluit.
• / 2: Dit deelt het resultaat door 2 omdat we elke diagonaal dubbel hebben geteld (van A naar C is hetzelfde als van C naar A).

De formule is dus een efficiënte manier om het aantal diagonalen in elke veelhoek te berekenen, ongeacht het aantal zijden.

Voorbeelden met Andere Veelhoeken

Om het concept verder te verduidelijken, laten we eens kijken naar enkele andere veelhoeken en het aantal diagonalen dat ze hebben:

• Driehoek (n=3): Aantal diagonalen = 3 * (3 - 3) / 2 = 3 * 0 / 2 = 0. Een driehoek heeft geen diagonalen.
• Vierhoek (n=4): Aantal diagonalen = 4 * (4 - 3) / 2 = 4 * 1 / 2 = 2. Een vierhoek heeft twee diagonalen.
• Vijfhoek (n=5): Aantal diagonalen = 5 * (5 - 3) / 2 = 5 * 2 / 2 = 5. Een vijfhoek heeft vijf diagonalen.

Je kunt zelf de formule toepassen op veelhoeken met nog meer zijden. Je zult zien dat het aantal diagonalen snel toeneemt naarmate het aantal zijden toeneemt.

Waarom is Dit Nuttig?

Je vraagt je misschien af: "Waarom is het belangrijk om te weten hoeveel diagonalen een zeshoek heeft?" Hoewel het misschien geen direct praktisch nut heeft in het dagelijks leven, helpt het begrijpen van deze concepten je analytisch denken en probleemoplossende vaardigheden te ontwikkelen.

Daarnaast is meetkunde een fundamenteel onderdeel van de wiskunde, en het begrijpen van de basisprincipes is essentieel voor het bestuderen van meer geavanceerde onderwerpen. Dit soort kennis kan van pas komen bij vakken als architectuur, engineering, computer graphics en zelfs kunst.

Bovendien kan het oplossen van dit soort problemen je nieuwsgierigheid prikkelen en je aanmoedigen om de wereld om je heen op een andere manier te bekijken. Je begint patronen en relaties te zien die je anders misschien over het hoofd zou zien.

Conclusie: De Kracht van de Meetkunde

We hebben in dit artikel ontdekt dat een zeshoek 9 diagonalen heeft. We hebben dit aangetoond door middel van een intuïtieve aanpak en door het gebruik van een algemene formule. We hebben ook gekeken naar voorbeelden met andere veelhoeken en besproken waarom het begrijpen van deze concepten nuttig kan zijn.

Het bestuderen van meetkunde is meer dan alleen het leren van formules en het oplossen van problemen. Het gaat om het ontwikkelen van een manier van denken die je helpt om de wereld om je heen te begrijpen en te waarderen. Dus de volgende keer dat je een zeshoek ziet, denk dan even aan de 9 diagonalen die erin verborgen zitten!

We hopen dat dit artikel je heeft geholpen om het concept van diagonalen in een zeshoek te begrijpen. Blijf leren, blijf ontdekken en blijf nieuwsgierig!