Hoeveel Diagonalen Heeft Een Zevenhoek
Heb je je ooit afgevraagd hoeveel diagonalen een zevenhoek heeft? Het lijkt misschien een simpele geometrische vraag, maar voor velen kan het lastig zijn om dit direct uit te rekenen. Misschien zit je vast met een wiskunde huiswerkopdracht, ben je een docent die een uitleg zoekt, of gewoon nieuwsgierig naar geometrie. Wat de reden ook is, we gaan je helpen om dit raadsel op te lossen en de logica erachter te begrijpen.
Wat is een diagonaal eigenlijk?
Laten we beginnen bij de basis. Een diagonaal is een lijnstuk dat twee niet-opeenvolgende hoekpunten van een veelhoek verbindt. Met andere woorden, het is een lijn die binnen een figuur loopt en twee hoeken verbindt die niet direct naast elkaar liggen. Stel je voor dat je een ster tekent; de lijnen die je trekt zijn in feite diagonalen van de veelhoek die de ster vormt.
Het is belangrijk om het verschil te begrijpen tussen een zijde en een diagonaal. Een zijde verbindt twee opeenvolgende hoekpunten, en vormt zo de rand van de veelhoek. Een diagonaal daarentegen steekt als het ware over de figuur heen.
Waarom is dit belangrijk?
Je vraagt je misschien af: "Waarom zou ik dit willen weten?" Goede vraag! Geometrie is niet alleen een abstract vak in de wiskunde. Het zit overal om ons heen. Denk aan architectuur, kunst, design en zelfs gaming. Het begrijpen van de eigenschappen van veelhoeken, inclusief het aantal diagonalen, kan nuttig zijn bij:
- Bouwkundig ontwerp: Diagonalen spelen een cruciale rol in de stabiliteit van constructies, bijvoorbeeld in bruggen en dakconstructies.
- Computergraphics: Bij het renderen van 3D-modellen worden veelhoeken, waaronder zevenhoeken, gebruikt. Het begrijpen van hun eigenschappen is essentieel voor efficiënte rendering.
- Probleemoplossing: Het aanpakken van geometrische problemen traint je logisch denkvermogen en probleemoplossende vaardigheden, die van pas komen in allerlei situaties.
Kortom, geometrie is meer dan alleen formules en figuren. Het is een manier om de wereld om ons heen te begrijpen en te analyseren.
De formule voor het aantal diagonalen
Gelukkig is er een formule die ons helpt om het aantal diagonalen van een veelhoek te berekenen. De formule is als volgt:
n(n - 3) / 2
Waar n staat voor het aantal zijden (en dus ook het aantal hoekpunten) van de veelhoek.
Deze formule werkt omdat:
- n(n - 3): Vanuit elk hoekpunt kunnen we een diagonaal trekken naar alle andere hoekpunten, behalve naar zichzelf en de twee direct aangrenzende hoekpunten. Dus dat zijn n - 3 mogelijkheden. We vermenigvuldigen dit met het totale aantal hoekpunten (n).
- / 2: Omdat we elke diagonaal twee keer tellen (één keer van het ene uiteinde en één keer van het andere uiteinde), delen we het resultaat door 2 om de dubbele telling te corrigeren.
De zevenhoek: Hoeveel diagonalen?
Nu we de formule hebben, kunnen we deze toepassen op een zevenhoek. Een zevenhoek heeft 7 zijden (en dus ook 7 hoekpunten). Dus n = 7.
Laten we de formule invullen:
7(7 - 3) / 2 = 7(4) / 2 = 28 / 2 = 14
Dus een zevenhoek heeft 14 diagonalen.
Visuele bevestiging
Hoewel de formule betrouwbaar is, kan het helpen om het visueel te begrijpen. Stel je een zevenhoek voor. Probeer vanuit één hoekpunt alle mogelijke diagonalen te tekenen. Je zult zien dat je vanuit dat hoekpunt 4 diagonalen kunt tekenen (niet naar zichzelf of de twee aangrenzende hoekpunten). Als je dit voor elk hoekpunt zou doen en de dubbele telling zou corrigeren, kom je uit op 14 diagonalen.
Stap voor stap uitleg met een zevenhoek:
- Hoekpunt A: Je kunt diagonalen tekenen naar hoekpunten C, D, E en F. (4 diagonalen)
- Hoekpunt B: Je kunt diagonalen tekenen naar hoekpunten D, E, F en G. (4 diagonalen)
- Hoekpunt C: Je kunt diagonalen tekenen naar hoekpunten E, F, G en A. (4 diagonalen)
- Hoekpunt D: Je kunt diagonalen tekenen naar hoekpunten F, G, A en B. (4 diagonalen)
- Hoekpunt E: Je kunt diagonalen tekenen naar hoekpunten G, A, B en C. (4 diagonalen)
- Hoekpunt F: Je kunt diagonalen tekenen naar hoekpunten A, B, C en D. (4 diagonalen)
- Hoekpunt G: Je kunt diagonalen tekenen naar hoekpunten B, C, D en E. (4 diagonalen)
In totaal hebben we 7 * 4 = 28 diagonalen geteld. Maar we hebben elke diagonaal twee keer geteld (bijvoorbeeld de diagonaal van A naar C en de diagonaal van C naar A). Daarom delen we het door 2: 28 / 2 = 14.
Counterpoints: Waarom de formule soms lastig te begrijpen is
Sommige mensen vinden de formule in eerste instantie verwarrend. Ze vragen zich bijvoorbeeld af waarom we precies 3 aftrekken van het aantal hoekpunten. Het is belangrijk om te onthouden dat we de twee aangrenzende hoekpunten en het hoekpunt zelf niet mee mogen tellen bij het tekenen van een diagonaal. Het aftrekken van 3 is dus cruciaal voor de correcte berekening.
Een andere veelvoorkomende verwarring is het delen door 2. Dit is noodzakelijk om de dubbele telling te voorkomen. Zonder deze correctie zouden we elke diagonaal twee keer tellen, wat tot een incorrect resultaat zou leiden.
Waarom dit relevant is in de praktijk
Hoewel het tellen van diagonalen misschien een theoretische oefening lijkt, zijn er praktische toepassingen. Bijvoorbeeld:
- Het ontwerpen van sterke constructies: In de bouw wordt de plaatsing van diagonalen gebruikt om de stabiliteit van structuren te garanderen. Denk aan de diagonalen in een vakwerkbrug of de verstevigingen in een frame van een fiets.
- Efficiënte routing in netwerken: In computernetwerken kan het begrip van diagonalen helpen bij het ontwerpen van efficiënte routes voor dataoverdracht.
- Optimalisatie van spellen: In game-ontwikkeling kunnen kennis van veelhoeken en hun eigenschappen helpen bij het optimaliseren van de rendering van objecten en omgevingen.
Het begrijpen van deze principes kan dus bijdragen aan innovatieve oplossingen in verschillende vakgebieden.
Oefening baart kunst
De beste manier om de formule te beheersen, is door te oefenen. Probeer het aantal diagonalen te berekenen voor verschillende veelhoeken, zoals een vierkant, een vijfhoek, een zeshoek en een achthoek. Controleer je antwoorden met online calculators of geometrie tools om zeker te zijn van je resultaten.
Door te oefenen word je niet alleen beter in het toepassen van de formule, maar ontwikkel je ook een dieper begrip van de geometrische principes die eraan ten grondslag liggen.
Conclusie
Het berekenen van het aantal diagonalen van een zevenhoek, of welke veelhoek dan ook, is een leuke en leerzame oefening die ons inzicht geeft in de fundamentele principes van geometrie. Met de formule n(n - 3) / 2 kunnen we dit probleem eenvoudig oplossen. En door de praktische toepassingen te begrijpen, realiseren we ons dat geometrie meer is dan alleen een abstract vak; het is een essentieel onderdeel van de wereld om ons heen.
Dus, nu je weet dat een zevenhoek 14 diagonalen heeft, waar ga jij deze kennis toepassen? Misschien in een creatief project, een bouwkundig ontwerp, of gewoon om indruk te maken op je vrienden met je wiskundige vaardigheden. Hoe dan ook, we hopen dat je deze uitleg nuttig en inspirerend vond!
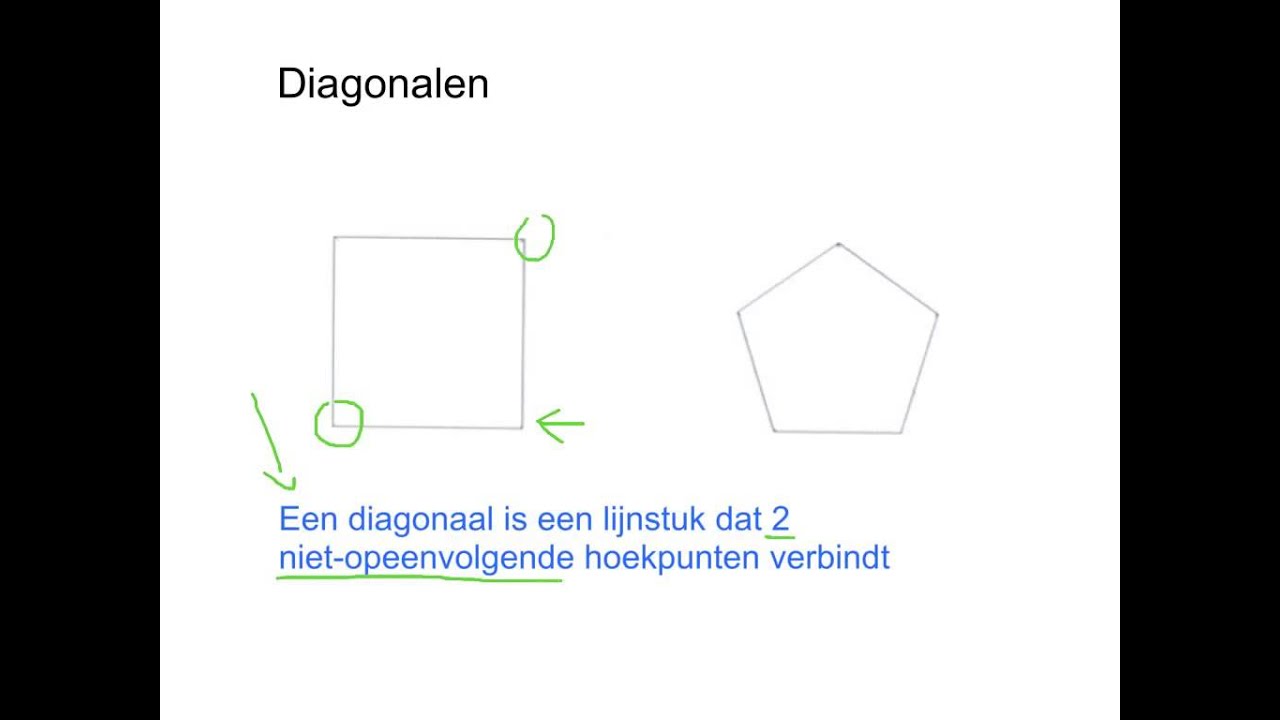
Bekijk ook deze gerelateerde berichten:
- Hoe Ga Je Om Met Stress
- Past Simple And Past Tense
- Welke Organen Links In Buik
- Hoe Lang Heeft Ddr Bestaan
- Hoeveel Procent Van De Asielzoekers Krijgt Een Verblijfsvergunning
- Blij Als Een Bij In De Zomerlucht
- Hoeveel Ml Is Een Gram
- Hoe Schrijf Je Curriculum Vitae
- Hoe Maakt Een Spin Zijn Eerste Draad
- Ti 84 Plus Ce T Uit Examenstand Met Computer
