Hoeveel Graden Heeft Een Driehoek

Heb je je ooit afgevraagd waarom bruggen zo sterk zijn? Of hoe architecten erin slagen gebouwen te ontwerpen die eeuwenlang meegaan? Het antwoord is verrassend simpel: de driehoek speelt hierin een cruciale rol. Maar voordat we in de fascinerende toepassingen duiken, moeten we eerst de basis begrijpen: hoeveel graden heeft een driehoek?

Dit is een vraag die velen zich in hun schooltijd hebben gesteld. En hoewel het antwoord vrij eenvoudig is, is het essentieel voor het begrijpen van meetkunde en vele praktische toepassingen in de echte wereld. Laten we dit samen uitzoeken, stap voor stap, op een manier die hopelijk niet aanvoelt als een wiskundeles uit het verleden!

De Magische Som: 180 Graden

Het antwoord op de vraag "Hoeveel graden heeft een driehoek?" is onomstotelijk: 180 graden. Simpel, toch? Maar wat betekent dit nu precies? Het betekent dat, ongeacht de vorm of grootte van de driehoek, de som van de drie hoeken in de driehoek altijd 180 graden zal zijn.

Stel je een driehoek voor met hoeken van 60, 60 en 60 graden. Dat is een gelijkzijdige driehoek. Als je deze hoeken bij elkaar optelt, krijg je 60 + 60 + 60 = 180 graden. Maar wat als de driehoek er heel anders uitziet? Laten we een driehoek nemen met hoeken van 90, 45 en 45 graden. Dit is een rechthoekige driehoek. Ook hier geldt: 90 + 45 + 45 = 180 graden. Het werkt altijd!

Waarom is dit zo?

Je kunt je afvragen: waarom is dit precies 180 graden en niet een ander getal? Het antwoord ligt in de fundamentele principes van de Euclidische meetkunde. Een recht lijn, een basisconcept in de meetkunde, heeft een hoek van 180 graden. Je kunt een driehoek zien als een 'vervormde' rechte lijn die is 'gebogen' om een gesloten figuur te vormen. De hoeken die ontstaan door deze 'vervorming' moeten samen de oorspronkelijke 180 graden van de rechte lijn behouden.

Er zijn verschillende manieren om dit te bewijzen, maar een van de meest intuïtieve is om een driehoek te tekenen en de hoeken af te knippen. Als je de drie afgeknipt hoeken naast elkaar legt, vormen ze precies een rechte lijn, wat overeenkomt met 180 graden.

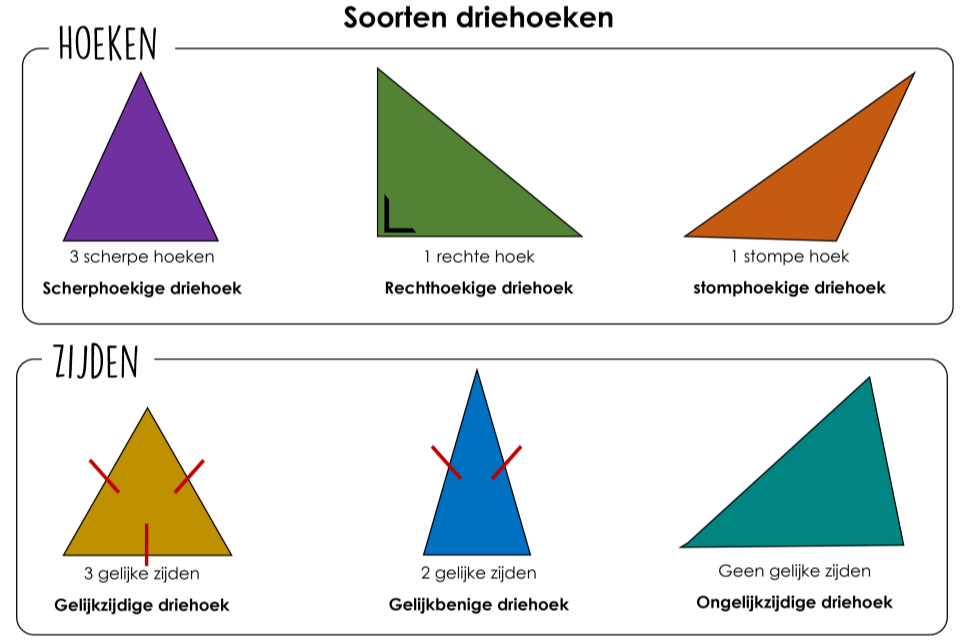
Verschillende Soorten Driehoeken

Nu we weten dat de som van de hoeken in een driehoek altijd 180 graden is, kunnen we kijken naar de verschillende soorten driehoeken en hoe deze regel van toepassing is.

• Gelijkzijdige Driehoek: Alle zijden zijn gelijk, en alle hoeken zijn gelijk (60 graden per hoek).
• Gelijkbenige Driehoek: Twee zijden zijn gelijk, en de twee hoeken tegenover deze zijden zijn ook gelijk.
• Ongelijkzijdige Driehoek: Alle zijden zijn verschillend, en alle hoeken zijn verschillend.
• Rechthoekige Driehoek: Heeft één hoek van 90 graden. De andere twee hoeken zijn samen 90 graden.
• Scherphoekige Driehoek: Alle hoeken zijn kleiner dan 90 graden.
• Stomphoekige Driehoek: Heeft één hoek groter dan 90 graden.

Het is belangrijk te onthouden dat, ongeacht het type driehoek, de som van de hoeken altijd 180 graden zal zijn. Dit is een fundamentele eigenschap van driehoeken in de Euclidische meetkunde.

De Impact in de Praktijk: Meer dan Alleen Wiskunde

Je vraagt je misschien af: "Waarom is dit belangrijk? Wat heb ik hieraan in het dagelijks leven?" Het antwoord is dat de eigenschappen van driehoeken overal om ons heen worden gebruikt, vaak zonder dat we het doorhebben.

• Architectuur: Driehoeken worden gebruikt in bruggen, daken en andere constructies om stabiliteit en sterkte te bieden. Denk aan de Eiffeltoren, een iconisch voorbeeld van een structuur die afhankelijk is van de sterkte van driehoeken.
• Constructie: Framebouw is afhankelijk van driehoeken voor de stabiliteit van muren en daken.
• Navigatie: Driehoeksmeting wordt gebruikt om afstanden en posities te bepalen, zowel op land als op zee. GPS-systemen gebruiken ook principes die gebaseerd zijn op driehoeksmeting.
• Game Development: In 3D-modellering worden objecten vaak opgebouwd uit polygonen, waarvan driehoeken de meest eenvoudige en efficiënte zijn.

De sterkte en stabiliteit van een driehoek komen voort uit het feit dat het de eenvoudigste polygon is die niet kan worden vervormd zonder de lengte van een van de zijden te veranderen. Dit maakt het een essentieel element in veel ontwerpen en constructies.

Counterpoints: Niet-Euclidische Meetkunde

Het is belangrijk om te vermelden dat de regel van 180 graden voor de som van de hoeken in een driehoek alleen geldt in de Euclidische meetkunde. Er bestaan ook niet-Euclidische meetkundes, zoals de sferische meetkunde (op het oppervlak van een bol) en de hyperbolische meetkunde. In deze meetkundes kan de som van de hoeken in een driehoek verschillen van 180 graden.

Bijvoorbeeld, op het oppervlak van een bol (zoals de aarde), kan de som van de hoeken in een driehoek groter zijn dan 180 graden. Dit komt doordat de lijnen (geodeten) op een bol gebogen zijn, in plaats van recht. Dit is essentieel om te begrijpen bij het maken van kaarten van de aarde.

Hoewel deze niet-Euclidische meetkundes minder alledaags zijn, zijn ze cruciaal in vakgebieden zoals algemene relativiteitstheorie en kosmologie, waar de kromming van de ruimte-tijd een belangrijke rol speelt.

Oefening Baart Kunst: Rekenen met Driehoeken

Laten we een paar voorbeelden bekijken om te oefenen met het toepassen van de regel van 180 graden:

• Voorbeeld 1: Een driehoek heeft hoeken van 70 graden en 50 graden. Wat is de grootte van de derde hoek?

  Oplossing: 180 - 70 - 50 = 60 graden.

• Voorbeeld 2: Een rechthoekige driehoek heeft één hoek van 30 graden. Wat is de grootte van de derde hoek?

  Oplossing: Aangezien het een rechthoekige driehoek is, weten we dat één hoek 90 graden is. Dus 180 - 90 - 30 = 60 graden.

• Voorbeeld 3: Een gelijkbenige driehoek heeft één hoek van 40 graden die niet tussen de twee gelijke zijden ligt. Wat zijn de groottes van de andere twee hoeken?

  Oplossing: De andere twee hoeken zijn gelijk aan elkaar. Noem de grootte van één van deze hoeken 'x'. Dan geldt: 40 + x + x = 180. Dus 2x = 140, en x = 70 graden.

Door te oefenen met dit soort problemen, zul je de regel van 180 graden beter begrijpen en kunnen toepassen in verschillende situaties.

Het Grotere Plaatje: Meer dan een Getal

Uiteindelijk is de kennis dat de som van de hoeken in een driehoek 180 graden is, meer dan alleen een feitelijkheid. Het is een bouwsteen voor het begrijpen van complexere meetkundige concepten en hun toepassingen in de echte wereld. Van de architectuur van imposante gebouwen tot de technologie achter onze navigatiesystemen, de eenvoudige driehoek speelt een cruciale rol.

Het is gemakkelijk om wiskundige concepten als irrelevant te beschouwen voor ons dagelijks leven. Maar hopelijk heeft dit artikel laten zien hoe zelfs een eenvoudig feit, zoals de som van de hoeken in een driehoek, een diepgaande invloed kan hebben op de wereld om ons heen.

Dus, de volgende keer dat je een brug oversteekt, een wolkenkrabber bewondert of je GPS gebruikt, denk dan eens aan de bescheiden driehoek en de magie van 180 graden.

Nu, met deze nieuwe kennis in je achterzak, hoe zou je de kracht van driehoeken kunnen gebruiken om iets te creëren of een probleem op te lossen in jouw eigen leven?