Hoeveel Grensvlakken Heeft Een Cilinder

Heb je je ooit afgevraagd hoeveel vlakken een simpele cilinder eigenlijk heeft? Het lijkt misschien een eenvoudige vraag, maar het antwoord is verrassender dan je denkt. Deze vraag komt vaak voor in wiskundelessen, puzzels en zelfs in de alledaagse engineering. In dit artikel gaan we dieper in op de geometrie van de cilinder en ontdekken we hoeveel grensvlakken (vlakken) het precies heeft. We richten ons op studenten, leraren, en iedereen die geïnteresseerd is in basisgeometrie. We zullen het concept op een heldere en begrijpelijke manier uitleggen, zodat je het gemakkelijk kunt begrijpen en onthouden.

Wat is een Cilinder?

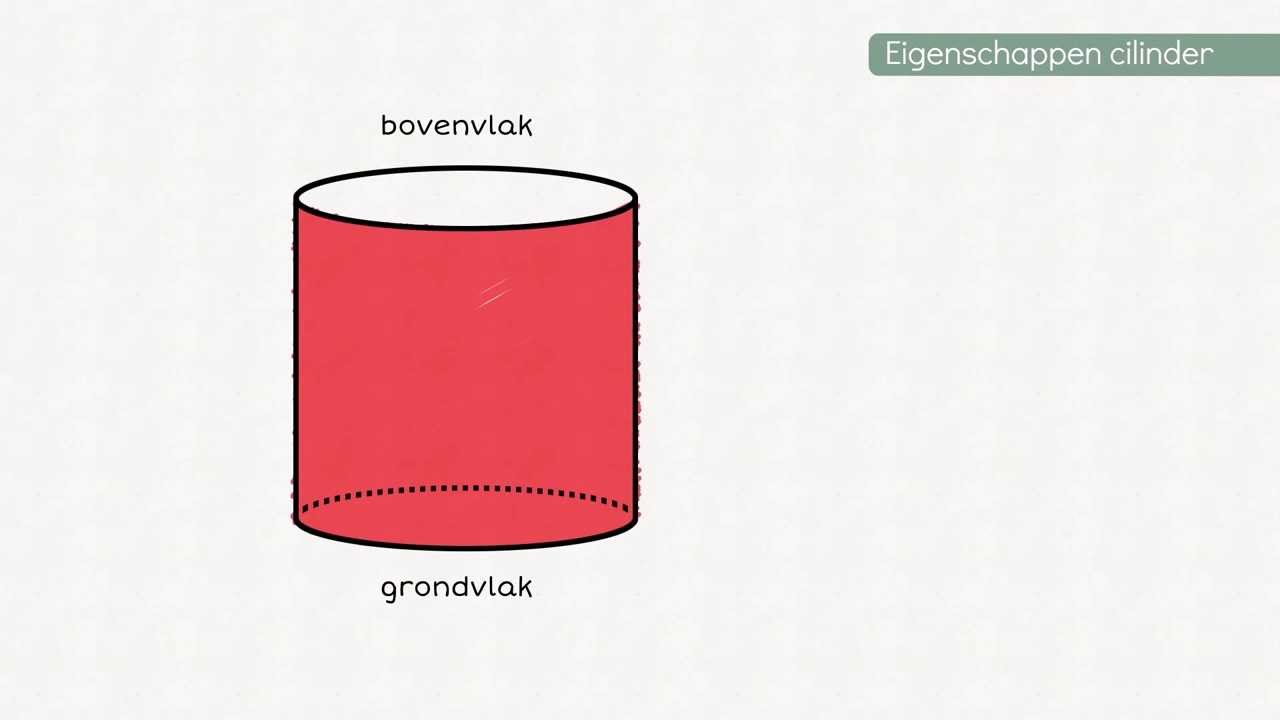
Laten we beginnen met de basis. Een cilinder is een driedimensionaal geometrisch object met twee identieke, evenwijdige cirkelvormige bases die verbonden zijn door een gebogen oppervlak. Denk aan een blik soep, een rol keukenpapier of een batterij. Al deze objecten benaderen de vorm van een cilinder. Het is cruciaal om de verschillende componenten van een cilinder te begrijpen voordat we kunnen bepalen hoeveel grensvlakken het heeft.

De Belangrijkste Componenten

Twee Cirkelvormige Bases: Dit zijn de twee platte, cirkelvormige uiteinden van de cilinder. Ze zijn perfect identiek en evenwijdig aan elkaar.
Gebogen Oppervlak: Dit is het oppervlak dat de twee cirkelvormige bases met elkaar verbindt. Het is een glad en continu oppervlak zonder hoeken of randen.

Hoeveel Grensvlakken heeft een Cilinder?

Nu komen we bij de hamvraag: hoeveel grensvlakken heeft een cilinder? Het antwoord is drie. Het is belangrijk om te begrijpen wat we precies bedoelen met een "grensvlak" in de geometrische context. Een grensvlak is een plat oppervlak dat een deel van een driedimensionaal object vormt.

Uitleg van de Grensvlakken

Het Eerste Cirkelvormige Grensvlak: Dit is de eerste cirkelvormige basis van de cilinder. Het is een plat vlak en dus een grensvlak.
Het Tweede Cirkelvormige Grensvlak: Dit is de tweede cirkelvormige basis van de cilinder. Net als de eerste, is dit ook een plat vlak en dus een grensvlak.
Het Gebogen Oppervlak (in een bepaalde context): Dit is waar de verwarring vaak ontstaat. Strikt genomen, een gebogen oppervlak is geen grensvlak in de zin van een plat vlak. Echter, in sommige contexten, vooral bij de benadering van de cilinder met behulp van polygonen (veelhoeken), wordt het gebogen oppervlak soms geconceptualiseerd als een oneindig aantal kleine, platte grensvlakken. Maar voor de fundamentele geometrie beschouwen we het gebogen oppervlak niet als een enkel grensvlak. In de context van oppervlakteberekening telt het gebogen oppervlak wel mee als een oppervlak, maar niet als een grensvlak in de letterlijke zin. Denk aan een kubus; die heeft zes duidelijke, platte grensvlakken. Een cilinder heeft er maar twee die echt plat zijn.

Dus, om het te herhalen: een standaard cilinder heeft twee platte, cirkelvormige grensvlakken en een gebogen oppervlak. Het gebogen oppervlak wordt meestal niet als een grensvlak geteld in de basisdefinitie, waardoor het totaal op twee komt. Echter, zoals hierboven beschreven, kan het in sommige gevallen als één oppervlak worden beschouwd bij het berekenen van de totale oppervlakte.

Waarom is dit Belangrijk?

Het begrijpen van de grensvlakken van een cilinder is belangrijk in verschillende disciplines, waaronder:

Wiskunde en Geometrie: Het is een basisconcept in de ruimtelijke meetkunde en helpt bij het begrijpen van complexere vormen en objecten.
Engineering: Ingenieurs gebruiken deze kennis bij het ontwerpen en construeren van verschillende objecten, van pijpleidingen tot containers.
Architectuur: Architecten passen geometrische principes toe om structuren te creëren die zowel esthetisch aantrekkelijk als functioneel zijn.
Computergraphics: Het modelleren van cilinders is essentieel in 3D-modellering en computervisualisatie.

Denk er eens over na: zonder een goed begrip van de geometrie van een cilinder, zou het moeilijk zijn om een blikje soep efficiënt te ontwerpen, een solide pijpleiding te bouwen of realistische 3D-modellen te maken. De basisbeginselen die we hier bespreken, vormen de bouwstenen voor complexere toepassingen.

Cilinders in het Dagelijks Leven

Cilinders zijn overal om ons heen! Laten we eens kijken naar enkele voorbeelden om het concept nog tastbaarder te maken:

Drankblikjes: De meeste frisdrank- en bierblikjes zijn cilindervormig. Dit ontwerp is efficiënt voor opslag en transport.
Pijpen: Waterleidingen, gasleidingen en afvoerbuizen zijn vaak cilindervormig. Dit zorgt voor een gemakkelijke doorstroming van vloeistoffen en gassen.
Kaarsen: Veel kaarsen hebben een cilindervorm, wat zorgt voor een stabiele en gelijkmatige verbranding.
Batterijen: De meeste batterijen zijn cilindervormig, wat een efficiënte manier is om chemische energie op te slaan.
Rollen Keukenpapier/Toiletpapier: De rol zelf is cilindervormig, en de inhoud is op een cilinder gewikkeld.

Als je de volgende keer naar een van deze objecten kijkt, bedenk dan dat je te maken hebt met een geometrische vorm met twee platte grensvlakken en een gebogen oppervlak!

Hoe Kun je dit Onthouden?

Het kan soms lastig zijn om te onthouden hoeveel grensvlakken een cilinder heeft. Hier zijn enkele tips om het gemakkelijker te maken:

Visualiseer: Stel je een blikje soep voor. Je ziet duidelijk de twee cirkelvormige deksels (de grensvlakken) en het gebogen oppervlak dat ze verbindt.
Maak een Tekening: Teken een cilinder en markeer de twee cirkelvormige bases. Dit visuele hulpmiddel kan helpen om het concept beter te begrijpen.
Gebruik een Ezelbruggetje: Bedenk een korte zin of woord dat je helpt om het aantal grensvlakken te onthouden. Bijvoorbeeld: "Cirkels Twee" (Cirkels staat voor de twee cirkels, en Twee voor het aantal grensvlakken).
Oefen: Oefen met het identificeren van cilinders in je omgeving en bedenk hoeveel grensvlakken ze hebben.

Door deze tips te gebruiken, zul je het concept van de grensvlakken van een cilinder gemakkelijk onthouden.

De Oppervlakte van een Cilinder

Hoewel we ons tot nu toe hebben gericht op het aantal grensvlakken, is het ook nuttig om de oppervlakte van een cilinder te bespreken. De totale oppervlakte van een cilinder bestaat uit de oppervlakte van de twee cirkelvormige bases en de oppervlakte van het gebogen oppervlak.

De formule voor de oppervlakte van een cilinder is:

Oppervlakte = 2πr² + 2πrh

2πr²: Dit is de oppervlakte van de twee cirkelvormige bases (πr² voor elke basis).
2πrh: Dit is de oppervlakte van het gebogen oppervlak, waarbij 'r' de straal van de basis is en 'h' de hoogte van de cilinder.

Het is belangrijk om te onthouden dat, hoewel het gebogen oppervlak geen grensvlak is in de strikte zin van het woord, het wel bijdraagt aan de totale oppervlakte van de cilinder. In de context van oppervlakteberekeningen wordt het gebogen oppervlak beschouwd als een integraal onderdeel van de totale oppervlakte.

Conclusie

We hebben geleerd dat een cilinder twee platte, cirkelvormige grensvlakken heeft en een gebogen oppervlak. Hoewel het gebogen oppervlak geen grensvlak is in de strikte zin, is het belangrijk voor het begrijpen van de vorm en het berekenen van de oppervlakte van de cilinder. Dit concept is essentieel in de wiskunde, engineering, architectuur en vele andere disciplines. Door de voorbeelden uit het dagelijks leven en de geheugentips, hopen we dat je nu een beter begrip hebt van de geometrie van de cilinder.

Dus, de volgende keer dat je een blikje soep, een pijp of een batterij ziet, kun je nadenken over de geometrische eigenschappen van deze alledaagse objecten. Geometrie is overal om ons heen, en door de basisprincipes te begrijpen, kunnen we de wereld om ons heen beter waarderen!