Hoeveel Zijden Heeft Een Piramide

Heb je je ooit afgevraagd hoeveel vlakken zo’n imposante piramide nu eigenlijk heeft? Het antwoord lijkt misschien simpel, maar er zit meer achter dan je in eerste instantie denkt. Veel mensen worstelen met dit concept, vooral omdat er verschillende soorten piramides bestaan, elk met een eigen aantal zijden. We gaan deze ingewikkelde vormen samen ontrafelen, zodat je straks precies weet hoe het zit.

De Basis: Wat is een Piramide?

Laten we beginnen met de basis. Een piramide is een veelvlak, een 3D-vorm, met een veelhoekige basis en driehoekige zijvlakken die samenkomen in een punt, de top. Het aantal zijden hangt dus direct af van de vorm van de basis.

Het Belang van de Basis

De vorm van de basis is cruciaal. Denk aan een huis: het fundament bepaalt alles wat erop gebouwd wordt. Zo is het ook met piramides. Een piramide met een vierkante basis is heel anders dan een met een driehoekige basis.

Verschillende Soorten Piramides

Hier zijn een paar veelvoorkomende voorbeelden:

• Driehoekige Piramide (Tetraëder): Heeft een driehoek als basis.
• Vierkante Piramide: Heeft een vierkant als basis.
• Vijfhoekige Piramide: Heeft een vijfhoek als basis.
• Zeshoekige Piramide: Heeft een zeshoek als basis.

Hoeveel Zijden Heeft Elke Piramide Nu Precies?

Laten we elk type piramide eens onder de loep nemen en uitrekenen hoeveel zijden ze hebben. Denk eraan: elk zijvlak is een vlak.

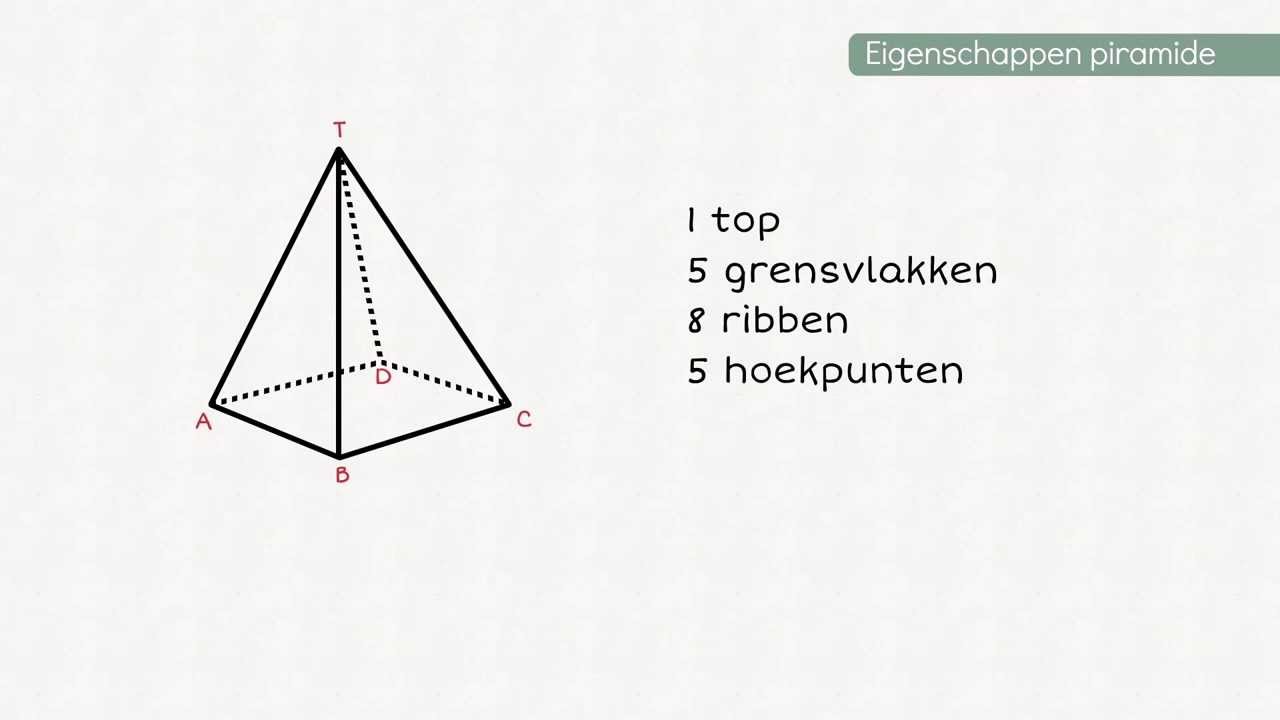
De Driehoekige Piramide (Tetraëder)

De driehoekige piramide, ook wel een tetraëder genoemd, heeft een driehoekige basis en drie driehoekige zijvlakken. Dat betekent:

• 1 driehoekige basis
• 3 driehoekige zijvlakken
• Totaal: 4 zijden

Dit is de eenvoudigste vorm van een piramide. Je kunt je voorstellen dat dit als een soort 'bouwpakket' piramide is - heel basic, maar wel een echte piramide.

De Vierkante Piramide

De vierkante piramide heeft een vierkante basis en vier driehoekige zijvlakken. Dus:

• 1 vierkante basis
• 4 driehoekige zijvlakken
• Totaal: 5 zijden

Dit is de meest bekende vorm, denk maar aan de piramides in Egypte! Ze zijn indrukwekkend en een perfect voorbeeld van hoe de basis de hele structuur bepaalt.

De Vijfhoekige Piramide

Nu wordt het iets lastiger. De vijfhoekige piramide heeft een vijfhoekige basis en vijf driehoekige zijvlakken:

• 1 vijfhoekige basis
• 5 driehoekige zijvlakken
• Totaal: 6 zijden

Stel je voor dat je een snoepje in de vorm van een vijfhoekige piramide hebt. Lekker toch?

De Zeshoekige Piramide

Tenslotte, de zeshoekige piramide heeft een zeshoekige basis en zes driehoekige zijvlakken:

• 1 zeshoekige basis
• 6 driehoekige zijvlakken
• Totaal: 7 zijden

Zoals je ziet, het patroon is duidelijk. Elke keer als we een zijde aan de basis toevoegen, voegen we ook een zijde toe aan het totale aantal zijden van de piramide.

De Formule Achter het Aantal Zijden

Als je het patroon ziet, kun je het generaliseren. Voor een piramide met een *n*-hoekige basis geldt de volgende formule:

Aantal zijden = n + 1

Dus, als je een piramide hebt met een achthoekige basis, dan heeft deze 8 + 1 = 9 zijden.

Waarom is Dit Nuttig om te Weten?

Misschien denk je: "Leuk hoor, al die wiskunde, maar wat heb ik eraan?" Nou, kennis van geometrische vormen is essentieel in veel beroepen. Denk aan:

• Architectuur: Voor het ontwerpen van gebouwen en structuren.
• Engineering: Voor het berekenen van sterkte en stabiliteit.
• Grafisch ontwerp: Voor het creëren van visuele elementen.
• Game development: Voor het modelleren van 3D-werelden.

Zelfs als je geen van deze beroepen ambieert, helpt het je om ruimtelijk inzicht te ontwikkelen, wat handig is bij het inpakken van dozen, het monteren van meubels, of gewoon het begrijpen van de wereld om je heen.

Misverstanden en Tegenargumenten

Sommige mensen verwarren zijden vaak met ribben (de lijnen waar de zijden samenkomen) of hoekpunten (de punten waar de ribben samenkomen). Het is belangrijk om deze termen goed uit elkaar te houden. Ook denken sommigen dat alle piramides vierkant zijn, maar dat is dus absoluut niet waar!

Een ander tegenargument is dat het allemaal erg theoretisch is. Maar zelfs theoretische kennis kan praktisch worden toegepast. Bijvoorbeeld, in de bouw wordt er constant gerekend met geometrische vormen om ervoor te zorgen dat een gebouw stevig en veilig is.

Oplossingsgericht Denken

In plaats van alleen te praten over het aantal zijden, kunnen we ook kijken naar hoe we piramides kunnen bouwen! Denk aan het bouwen van een modelpiramide met karton of LEGO. Dit is een leuke en educatieve manier om de theorie in de praktijk te brengen.

Daarnaast zijn er talloze online tools en simulaties waarmee je verschillende soorten piramides kunt visualiseren en manipuleren. Dit maakt het leren interactiever en leuker.

Conclusie

Het aantal zijden van een piramide hangt dus volledig af van de vorm van de basis. Van de simpele tetraëder met 4 zijden tot de complexere vormen met een vijfhoekige of zeshoekige basis, elke piramide is uniek. Door de formule te begrijpen, kun je eenvoudig het aantal zijden berekenen, ongeacht de vorm van de basis.

Hopelijk heb je nu een beter begrip van piramides en hun zijden. Is er een specifiek type piramide waar je meer over wilt weten? Of ga je zelf aan de slag met het bouwen van een modelpiramide?