Hoogte Van Een Driehoek Berekenen

Heb je ooit voor een project gestaan, of dat nu een schoolopdracht is, een doe-het-zelf project in huis, of zelfs een complexere berekening in de wiskunde of bouwkunde, waarbij je de hoogte van een driehoek nodig had? Misschien voelde je je overweldigd, alsof je een onbekend terrein betrad. Dat gevoel is heel normaal. Veel mensen worstelen met meetkundige concepten, vooral als het gaat om het correct toepassen van de juiste formules.

Maar wees gerust, de hoogte van een driehoek berekenen is minder ingewikkeld dan het op het eerste gezicht lijkt. In dit artikel gaan we dieper in op de verschillende manieren om de hoogte van een driehoek te berekenen, en we leggen uit hoe je deze kennis in de praktijk kunt toepassen. We zullen verschillende scenario's bekijken, van de meest eenvoudige tot de wat meer uitdagende.

Waarom is de Hoogte van een Driehoek Belangrijk?

De hoogte van een driehoek is niet zomaar een wiskundig concept; het heeft reële toepassingen in verschillende vakgebieden. Denk aan:

• Bouwkunde: Bij het berekenen van dakoppervlaktes, de stabiliteit van constructies en het ontwerpen van gebouwen.
• Landmeetkunde: Bij het bepalen van de oppervlakte van stukken land of het uitzetten van grenzen.
• Engineering: Bij het ontwerpen van bruggen, machines en andere structuren waar de stabiliteit en kracht van driehoeken essentieel zijn.
• Gaming en Graphics: Bij het renderen van 3D-modellen, waarbij driehoeken de basis vormen van complexe objecten.
• Alledaagse situaties: Zelfs bij het inlijsten van een foto of het snijden van een taart kan de kennis van driehoeken van pas komen.

Kortom, het begrijpen van hoe je de hoogte van een driehoek kunt berekenen, opent deuren naar een breed scala aan praktische toepassingen.

Wat is de Hoogte van een Driehoek Eigenlijk?

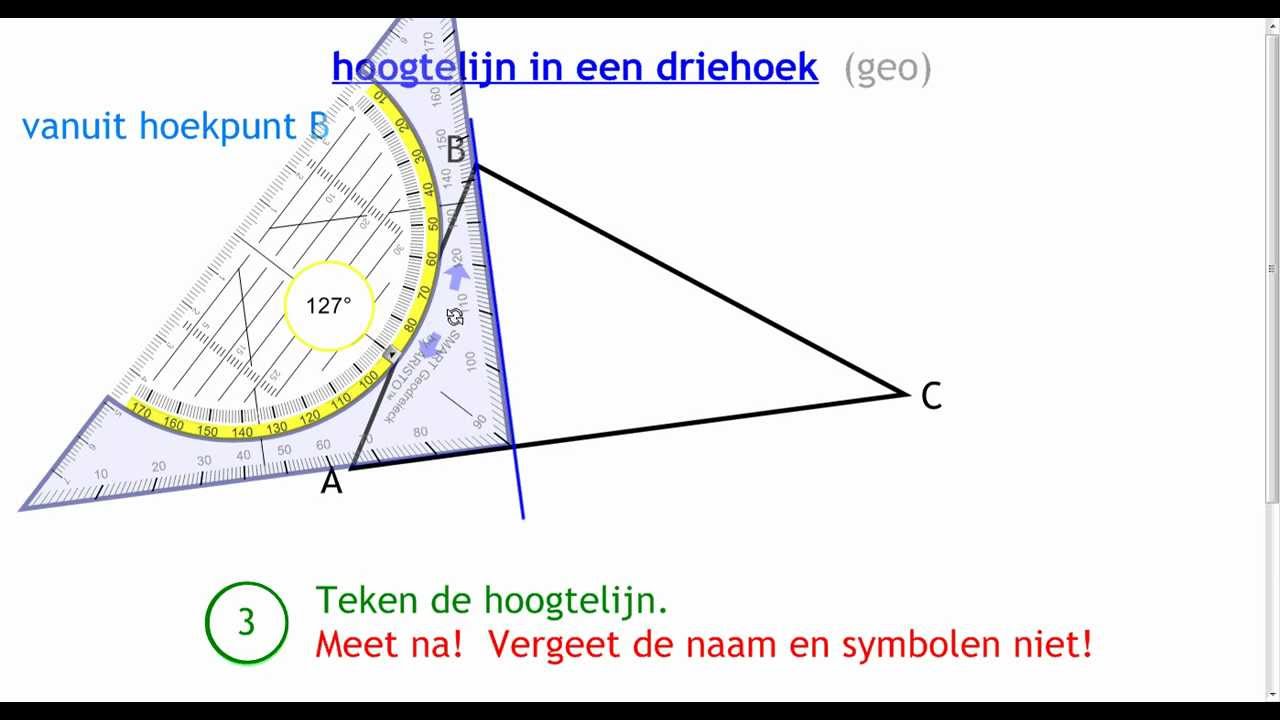
De hoogte van een driehoek is de loodrechte afstand van een hoekpunt naar de tegenoverliggende zijde (de basis). Het is belangrijk om te benadrukken dat de hoogte altijd loodrecht (onder een hoek van 90 graden) op de basis staat. Elke driehoek heeft drie mogelijke hoogtes, afhankelijk van welke zijde je als basis beschouwt.

Stel je een driehoek voor die op een van zijn zijden staat. De hoogte is dan de afstand van het hoogste punt (het tegenoverliggende hoekpunt) naar de grond (de basis). Als de driehoek niet recht staat, moet je de hoogte ‘laten zakken’ tot een punt op de basis of een verlenging ervan.

Methoden om de Hoogte van een Driehoek te Berekenen

Er zijn verschillende manieren om de hoogte van een driehoek te berekenen, afhankelijk van de informatie die je al hebt. We bespreken de meest voorkomende methoden:

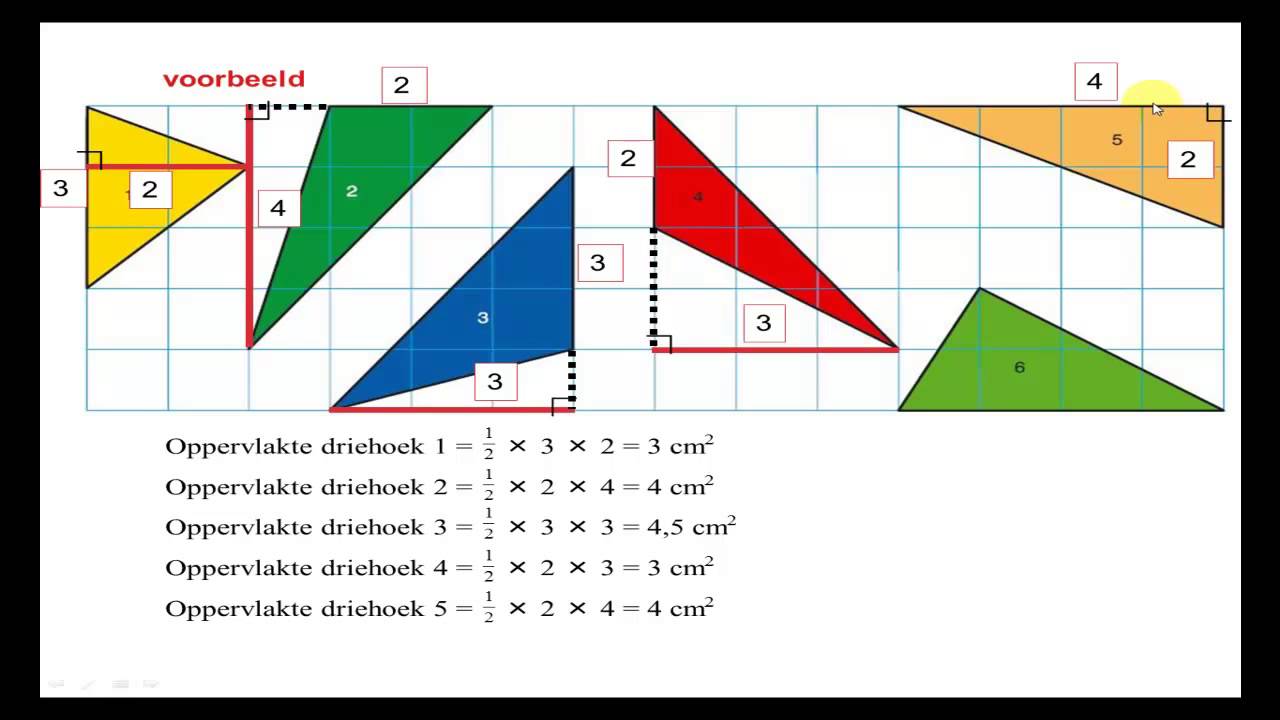
1. Met behulp van de Oppervlakteformule

Als je de oppervlakte (A) en de lengte van de basis (b) van de driehoek kent, kun je de hoogte (h) berekenen met de volgende formule:

A = (1/2) * b * h

Om de hoogte te vinden, herschrijven we de formule als:

h = (2 * A) / b

Voorbeeld: Stel dat de oppervlakte van een driehoek 20 cm² is en de basis 8 cm. Dan is de hoogte: h = (2 * 20) / 8 = 5 cm.

2. Met behulp van de Stelling van Pythagoras (voor Rechthoekige Driehoeken)

De Stelling van Pythagoras (a² + b² = c²) is een krachtig hulpmiddel, maar alleen toepasbaar op rechthoekige driehoeken (driehoeken met een rechte hoek van 90 graden). In een rechthoekige driehoek is één van de zijden (de zijde tegenover de rechte hoek, de hypotenusa) altijd langer dan de andere twee zijden (de rechthoekszijden). Als je de lengte van de hypotenusa en één rechthoekszijde kent, kun je de andere rechthoekszijde berekenen, en deze kan dienen als de hoogte (als je de andere rechthoekszijde als basis beschouwt).

Voorbeeld: In een rechthoekige driehoek is de hypotenusa 13 cm en een rechthoekszijde 5 cm. De andere rechthoekszijde (die we als hoogte kunnen beschouwen) is dan: √(13² - 5²) = √(169 - 25) = √144 = 12 cm.

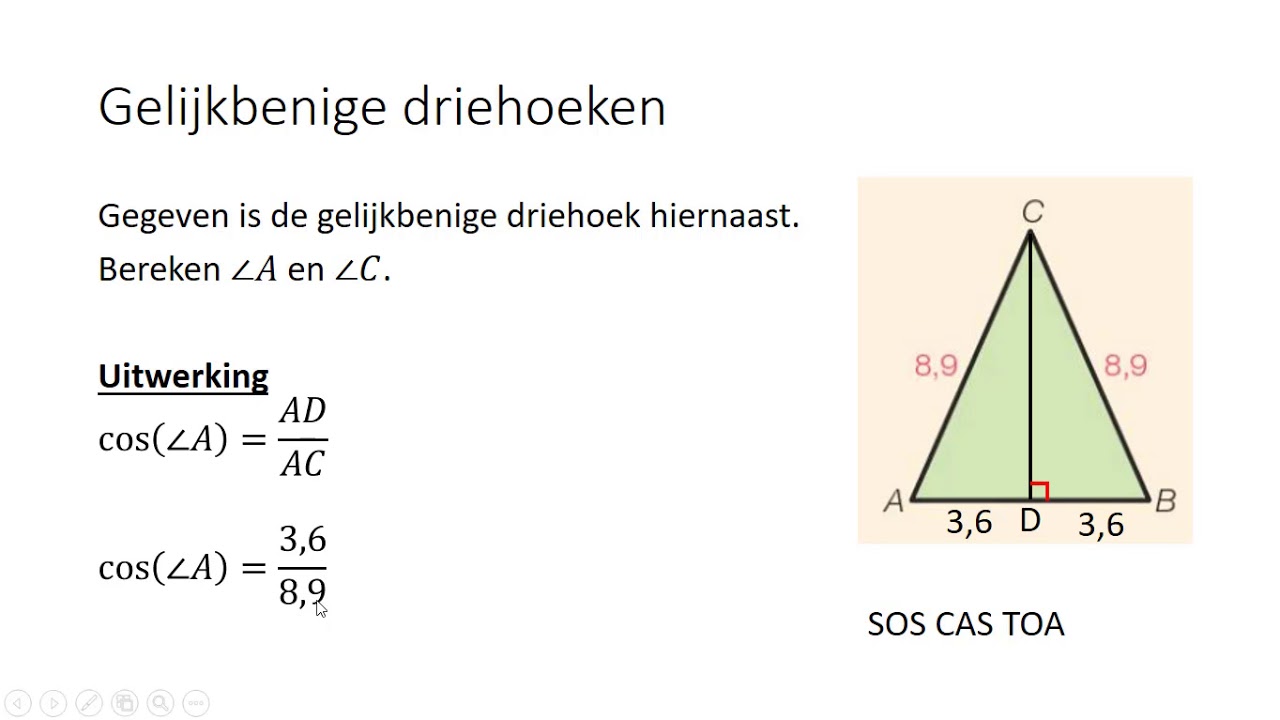
3. Met behulp van Trigonometrie (Sinus, Cosinus, Tangens)

Trigonometrie is handig als je een hoek en de lengte van een zijde van de driehoek kent. De sinusfunctie (sin) is hierbij vaak nuttig. De sinus van een hoek is gelijk aan de overstaande zijde gedeeld door de schuine zijde (hypotenusa).

Als je een hoek (θ) en de lengte van de schuine zijde (c) kent, dan is de hoogte (h) ten opzichte van de basis die aan die hoek grenst:

h = c * sin(θ)

Voorbeeld: Stel dat een hoek in een driehoek 30 graden is en de schuine zijde (hypotenusa) 10 cm. Dan is de hoogte: h = 10 * sin(30°) = 10 * 0.5 = 5 cm. (Let op: je rekenmachine moet in de juiste modus staan (graden of radialen)).

4. Met behulp van de Formule van Heron

De Formule van Heron is handig als je de lengtes van alle drie de zijden van de driehoek kent, maar geen hoeken of de oppervlakte. Deze formule stelt je in staat om eerst de oppervlakte van de driehoek te berekenen, waarna je de hoogte kunt bepalen met behulp van de oppervlakteformule (zoals besproken in punt 1).

Eerst bereken je de semi-perimeter (s) van de driehoek:

s = (a + b + c) / 2

Waar a, b, en c de lengtes van de drie zijden zijn. Vervolgens bereken je de oppervlakte (A) met de formule:

A = √(s * (s - a) * (s - b) * (s - c))

Zodra je de oppervlakte hebt, kun je de hoogte berekenen met behulp van de formule h = (2 * A) / b, waarbij je één van de zijden als basis (b) kiest.

Voorbeeld: Stel dat de zijden van een driehoek 5 cm, 7 cm en 8 cm zijn. Eerst berekenen we de semi-perimeter: s = (5 + 7 + 8) / 2 = 10 cm. Vervolgens berekenen we de oppervlakte: A = √(10 * (10 - 5) * (10 - 7) * (10 - 8)) = √(10 * 5 * 3 * 2) = √300 ≈ 17.32 cm². Als we de zijde van 8 cm als basis kiezen, dan is de hoogte: h = (2 * 17.32) / 8 ≈ 4.33 cm.

Counterpoints en Alternatieve Methoden

Sommige mensen beweren dat er snellere of eenvoudigere manieren zijn om de hoogte van een driehoek te berekenen, bijvoorbeeld door gebruik te maken van geavanceerde software of online calculators. Hoewel deze hulpmiddelen zeker hun waarde hebben, is het essentieel om de onderliggende principes te begrijpen. Zonder dit begrip loop je het risico op verkeerde interpretaties en blinde vlekken, vooral wanneer je te maken krijgt met onverwachte situaties of complexe problemen.

Er zijn ook grafische methoden, waarbij je de driehoek tekent en de hoogte meet. Hoewel dit visueel aantrekkelijk kan zijn, is het doorgaans minder nauwkeurig dan de wiskundige methoden, vooral bij kleine of complexe driehoeken.

Tips en Trucs

• Teken een schets: Maak altijd een schets van de driehoek om een visueel beeld te krijgen en de gegeven informatie te organiseren.
• Identificeer de beschikbare informatie: Bepaal welke informatie je al hebt (zijden, hoeken, oppervlakte) en kies de meest geschikte methode op basis daarvan.
• Controleer je antwoord: Zorg ervoor dat je antwoord logisch is. De hoogte kan bijvoorbeeld niet langer zijn dan de langste zijde van de driehoek.
• Wees consistent met eenheden: Gebruik dezelfde eenheden (bijv. centimeters, meters) voor alle metingen.
• Oefening baart kunst: Hoe meer je oefent met het berekenen van de hoogte van driehoeken, hoe sneller en zelfverzekerder je wordt.

Samenvatting

Het berekenen van de hoogte van een driehoek is een fundamentele vaardigheid met tal van praktische toepassingen. We hebben verschillende methoden besproken, waaronder het gebruik van de oppervlakteformule, de stelling van Pythagoras, trigonometrie en de formule van Heron. De keuze van de juiste methode hangt af van de beschikbare informatie. Onthoud dat het essentieel is om de onderliggende principes te begrijpen en te oefenen om de vaardigheid te beheersen.

Door de juiste aanpak te kiezen en de formules correct toe te passen, kan iedereen de hoogte van een driehoek berekenen, ongeacht de complexiteit. En door deze vaardigheid te beheersen, open je deuren naar een breed scala aan praktische toepassingen, van bouwkunde tot gaming.

We hopen dat dit artikel je heeft geholpen om de hoogte van een driehoek beter te begrijpen.

Ben je nu klaar om je nieuw verworven kennis in de praktijk te brengen en een paar oefenopgaven te maken? Of wil je wellicht andere meetkundige concepten verder verkennen?