Oppervlakte Driehoek Berekenen Met 3 Zijden

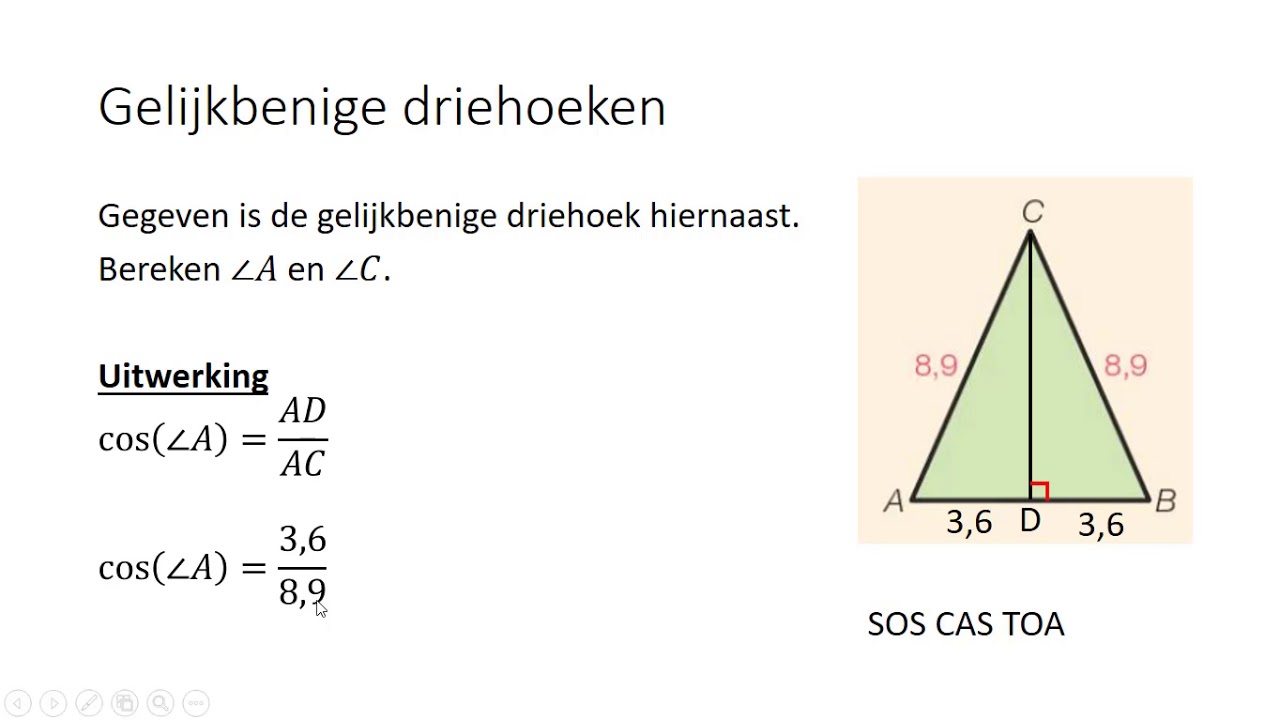
Heb je ooit voor een uitdaging gestaan waarbij je de oppervlakte van een driehoek moest berekenen, maar je had alleen de lengtes van de zijden? Geen zorgen, je bent niet de enige! Veel mensen vinden dit lastig, vooral als ze geen directe hoogtelijn hebben. We begrijpen dat het soms frustrerend kan zijn om vast te lopen op zo'n ogenschijnlijk simpele opgave. Maar geloof ons, er is een elegante oplossing: de formule van Heron. Laten we samen deze wiskundige uitdaging overwinnen!

Waarom is de oppervlakte van een driehoek berekenen belangrijk?

Je vraagt je misschien af: wanneer heb ik dit in het echte leven nou écht nodig? Nou, verrassend genoeg komt het vaker voor dan je denkt. Denk aan:

• Architectuur en Bouw: Architecten en bouwkundigen gebruiken driehoeken in hun ontwerpen voor stabiliteit en esthetiek. Het berekenen van de oppervlakte is cruciaal voor het bepalen van de hoeveelheid materiaal die nodig is.
• Landmeten: Landmeters gebruiken driehoeksmeting om land te verdelen en in kaart te brengen. De oppervlakte van deze driehoeken is essentieel voor het bepalen van eigendomsgrenzen.
• Engineering: Ingenieurs gebruiken driehoeken in de constructie van bruggen, daken en andere structuren. De oppervlakteberekening helpt bij het bepalen van de belasting en stabiliteit.
• Tuinieren en Landschapsarchitectuur: Bij het ontwerpen van tuinen en landschappen kan het handig zijn om de oppervlakte van driehoekige perken of gazons te berekenen voor het plannen van beplanting en het bestellen van de juiste hoeveelheid materialen.

Kortom, het berekenen van de oppervlakte van een driehoek is meer dan alleen een wiskundige oefening. Het is een praktische vaardigheid met toepassingen in diverse vakgebieden die ons dagelijks leven beïnvloeden.

De Formule van Heron: Een Elegante Oplossing

De formule van Heron, ook wel de formule van Hero genoemd, biedt een directe manier om de oppervlakte van een driehoek te berekenen als je de lengtes van de drie zijden kent. Laten we de formule eens bekijken:

Oppervlakte = √(s(s - a)(s - b)(s - c))

Waar:

• a, b en c de lengtes van de zijden van de driehoek zijn.
• s de halve omtrek is, berekend als: s = (a + b + c) / 2

Laten we deze formule eens toepassen op een concreet voorbeeld:

Voorbeeld: Een driehoek met zijden van 5 cm, 7 cm en 8 cm

1. Bereken de halve omtrek (s): s = (5 + 7 + 8) / 2 = 10 cm
2. Pas de formule van Heron toe: Oppervlakte = √(10(10 - 5)(10 - 7)(10 - 8)) = √(10 * 5 * 3 * 2) = √300 ≈ 17.32 cm²

Dus, de oppervlakte van de driehoek is ongeveer 17.32 vierkante centimeter.

Waarom Werkt de Formule van Heron?

De formule van Heron is afgeleid van trigonometrische principes, met name de cosinusregel. Hoewel de exacte afleiding complex kan zijn, is het belangrijk te begrijpen dat de formule wiskundig solide is. Het maakt gebruik van de relaties tussen de zijden en hoeken van een driehoek om de oppervlakte te berekenen zonder dat je de hoogte hoeft te weten.

Alternatieve Methoden en Hun Beperkingen

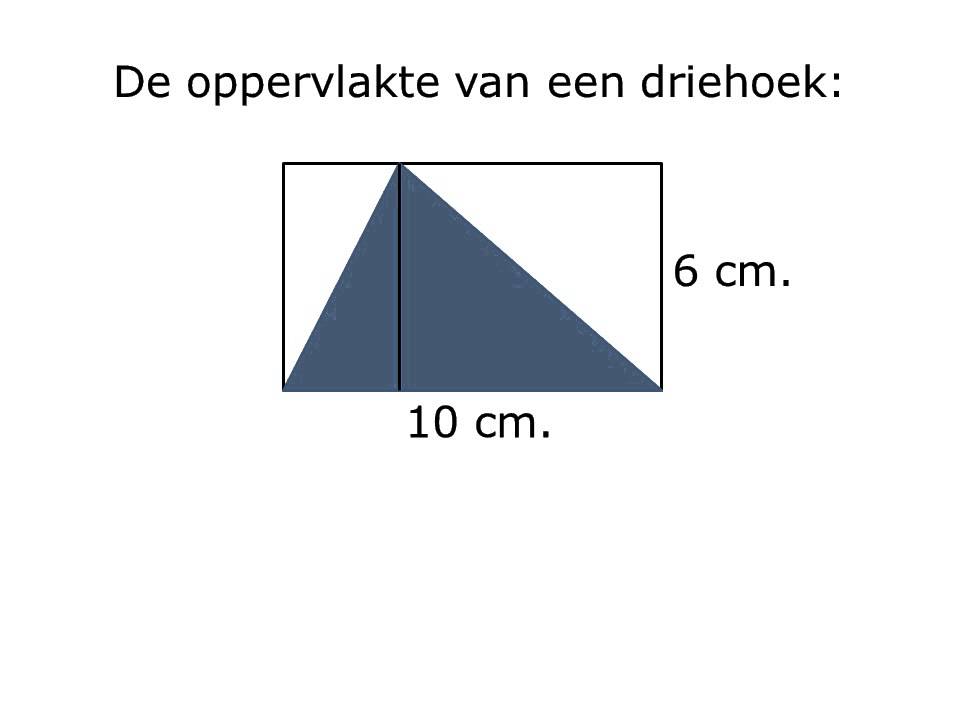
Natuurlijk zijn er andere manieren om de oppervlakte van een driehoek te berekenen. De meest bekende is waarschijnlijk de formule: Oppervlakte = (1/2) * basis * hoogte. Maar wat als je de hoogte niet weet? Hier komt de formule van Heron van pas. Andere methoden omvatten het gebruik van trigonometrie (sinusregel, cosinusregel) om hoeken te berekenen en vervolgens de oppervlakte te bepalen. Maar deze methoden zijn vaak complexer en vereisen meer gegevens dan alleen de zijdelengtes.

Een andere methode is het gebruik van coördinatengeometrie als je de coördinaten van de hoekpunten van de driehoek kent. Je kunt dan de afstand tussen de punten berekenen (om de zijden te vinden) en vervolgens de formule van Heron gebruiken, of je kunt direct de oppervlakte berekenen met behulp van een determinantformule. Echter, deze methode is alleen relevant als je de coördinaten van de hoekpunten hebt, wat niet altijd het geval is.

Mogelijke Valstrikken en Hoe Ze te Vermijden

Bij het gebruik van de formule van Heron zijn er een paar potentiële valkuilen waar je op moet letten:

• Foutieve Halve Omtrek: Een veelgemaakte fout is het verkeerd berekenen van de halve omtrek (s). Zorg ervoor dat je de som van alle zijden deelt door 2.
• Negatieve Waarden onder de Wortel: Als de waarden onder de wortel negatief zijn, betekent dit dat de ingevoerde zijdelengtes geen geldige driehoek vormen (de driehoek ongelijkheid stelling is niet voldaan: de som van twee zijden moet altijd groter zijn dan de derde zijde). Controleer je invoer!
• Rekenfouten: Zorg ervoor dat je nauwkeurig rekent, vooral bij het kwadrateren en worteltrekken. Het is handig om een rekenmachine te gebruiken om fouten te minimaliseren.
• Eenheden: Let op de eenheden! Als de zijden in centimeters zijn, is de oppervlakte in vierkante centimeters.

Tips voor een Succesvolle Berekening

Om de formule van Heron succesvol toe te passen, volgen hier enkele tips:

• Dubbelcheck je data: Zorg ervoor dat je de juiste lengtes van de zijden hebt.
• Gebruik een rekenmachine: Een rekenmachine helpt om nauwkeurig te rekenen en fouten te voorkomen.
• Schrijf tussenstappen op: Noteer de halve omtrek en de verschillende termen in de formule. Dit maakt het makkelijker om fouten op te sporen.
• Controleer je antwoord: Als je een onverwacht resultaat krijgt, controleer dan je berekeningen en de ingevoerde data.

De Formule van Heron in de Praktijk: Een Case Study

Stel je voor dat je een stuk land hebt in de vorm van een driehoek. Je wilt weten hoeveel graszaad je nodig hebt om het hele oppervlak te bedekken. Je meet de zijden en vindt dat ze 25 meter, 30 meter en 40 meter lang zijn. Met de formule van Heron kun je de oppervlakte berekenen en de benodigde hoeveelheid graszaad bepalen.

1. Bereken de halve omtrek (s): s = (25 + 30 + 40) / 2 = 47.5 meter
2. Pas de formule van Heron toe: Oppervlakte = √(47.5(47.5 - 25)(47.5 - 30)(47.5 - 40)) = √(47.5 * 22.5 * 17.5 * 7.5) ≈ 432.8 vierkante meter

Je weet nu dat je ongeveer 432.8 vierkante meter graszaad nodig hebt. Dit praktische voorbeeld illustreert hoe de formule van Heron je kan helpen bij alledaagse problemen.

Conclusie

De formule van Heron is een krachtig hulpmiddel om de oppervlakte van een driehoek te berekenen als je alleen de lengtes van de zijden kent. Het is een elegante en efficiënte oplossing die breed toepasbaar is in verschillende vakgebieden. Hoewel er alternatieve methoden zijn, biedt de formule van Heron een directe en betrouwbare manier om dit probleem op te lossen. Door de potentiële valkuilen te vermijden en de tips te volgen, kun je de formule met vertrouwen toepassen en nauwkeurige resultaten behalen.

Heb je nu meer vertrouwen in het berekenen van de oppervlakte van een driehoek met 3 bekende zijden? Welke andere wiskundige uitdagingen wil je graag aanpakken?