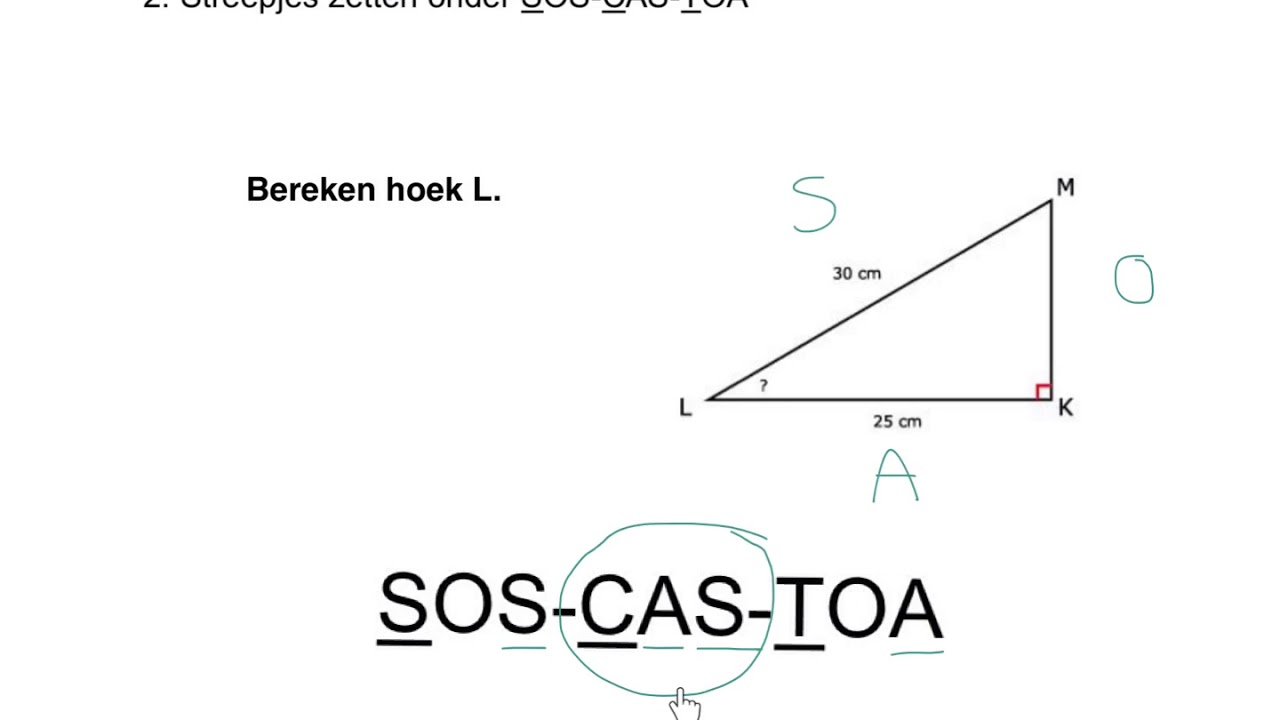
Schuine Zijde Berekenen Met Hoek

Je staat daar, te kijken naar dat dak. Je weet de hoek die het maakt met de grond, en je kent de hoogte van de muur. Maar hoe lang is die schuine kant eigenlijk? Dat is een vraag die veel mensen zich stellen, niet alleen bouwvakkers en wiskundeleraren, maar ook klussers, doe-het-zelvers en zelfs mensen die gewoon nieuwsgierig zijn naar de wereld om hen heen. Het berekenen van die schuine zijde, ofwel de hypotenusa, kan in eerste instantie intimiderend lijken, maar met een beetje uitleg en de juiste tools, is het verrassend eenvoudig.

Laten we eerlijk zijn, wiskunde was voor velen niet het favoriete vak op school. De formules en regels leken soms abstract en irrelevant. Maar in de praktijk kom je wiskundige principes vaker tegen dan je denkt. Denk aan het ophangen van een schilderij (zorg dat het recht hangt!), het bouwen van een vogelhuisje (zorg dat de hoeken kloppen!) of, inderdaad, het berekenen van de lengte van een dak (zorg dat het stevig is!). De schuine zijde berekenen is zo'n praktisch wiskundig probleem dat direct impact heeft op de dingen die je bouwt en maakt.

Waarom is dit belangrijk?

De impact van het correct berekenen van de schuine zijde reikt verder dan alleen het voorkomen van een scheef dak. Denk aan:

• Veiligheid: In de bouw is de juiste hoek en lengte cruciaal voor de stabiliteit van constructies. Een verkeerde berekening kan leiden tot instorting en gevaarlijke situaties.
• Efficiëntie: Het correct inschatten van de benodigde materialen bespaart tijd en geld. Je voorkomt verspilling en onnodige ritten naar de bouwmarkt.
• Esthetiek: Een goed gebouwde constructie ziet er simpelweg beter uit. Perfecte hoeken en lijnen dragen bij aan een professionele uitstraling.
• Functionaliteit: Of het nu gaat om een trap, een hellingbaan of een dak, de juiste afmetingen zorgen ervoor dat de constructie goed functioneert.

Stel je voor: je bent een schuur aan het bouwen. Je kent de hoogte van de muur (de overstaande zijde) en de hoek van het dak (bijvoorbeeld 30 graden). Als je de lengte van de schuine zijde (het dak) niet correct berekent, kan het dak te kort zijn, waardoor er regen binnenkomt, of te lang, waardoor het er lelijk uitziet en misschien zelfs niet goed past. Een kleine meetfout kan grote gevolgen hebben.

De Stelling van Pythagoras en Trigonometrie

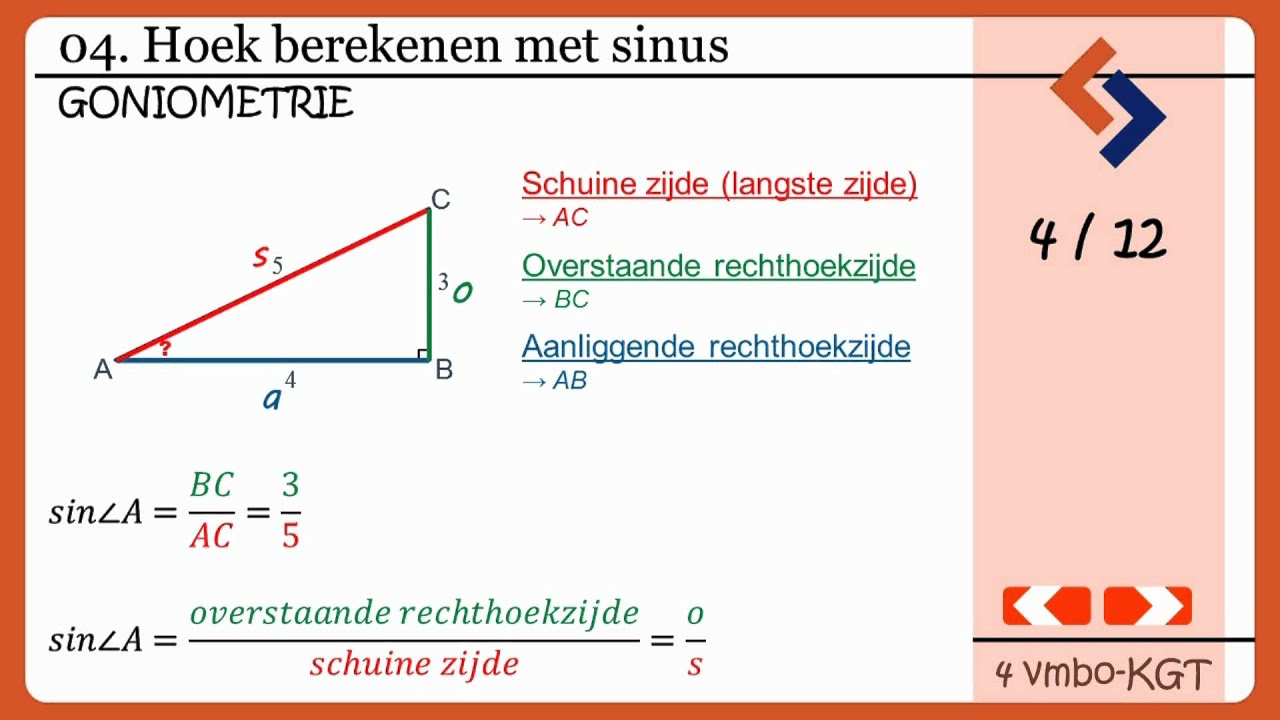
De meest bekende manier om de schuine zijde te berekenen is via de Stelling van Pythagoras: a² + b² = c². Deze stelling is echter alleen bruikbaar als je twee zijden van een rechthoekige driehoek kent. Als je alleen een hoek en één zijde weet, moet je overstappen op de trigonometrie.

Trigonometrie is de tak van de wiskunde die zich bezighoudt met de relaties tussen de hoeken en zijden van driehoeken. Binnen de trigonometrie zijn er drie belangrijke functies:

• Sinus (sin): Verhouding tussen de overstaande zijde en de schuine zijde (sin(hoek) = overstaande / schuine)
• Cosinus (cos): Verhouding tussen de aanliggende zijde en de schuine zijde (cos(hoek) = aanliggende / schuine)
• Tangens (tan): Verhouding tussen de overstaande zijde en de aanliggende zijde (tan(hoek) = overstaande / aanliggende)

Hoe werkt het in de praktijk?

Laten we teruggaan naar het voorbeeld van de schuur. Je weet de hoogte van de muur (de overstaande zijde, bijvoorbeeld 3 meter) en de hoek van het dak (bijvoorbeeld 30 graden). Je wilt de lengte van de schuine zijde weten.

Omdat je de overstaande zijde en de hoek weet, en je de schuine zijde wilt berekenen, gebruik je de sinus-functie:

sin(30°) = overstaande / schuine

sin(30°) = 3 / schuine

Om de schuine zijde te berekenen, herleid je de formule:

schuine = 3 / sin(30°)

De sinus van 30 graden is 0.5 (dit kun je opzoeken in een tabel of berekenen met een rekenmachine).

schuine = 3 / 0.5 = 6 meter

Dus de lengte van de schuine zijde van het dak is 6 meter.

Counterpoints en Misvattingen

Er zijn mensen die beweren dat je geen wiskunde nodig hebt om te klussen. "Meten is weten," zeggen ze, "en met een goede rolmaat kom je een heel eind." Hoewel meten belangrijk is, kan een gebrek aan wiskundig inzicht leiden tot fouten die makkelijk te vermijden waren. Een rolmaat kan je de lengte geven, maar niet de correctie voor de hoek.

Een andere misvatting is dat je een wiskunde genie moet zijn om dit te begrijpen. Niets is minder waar. Met een beetje oefening en een goede rekenmachine kan iedereen de basisprincipes van trigonometrie toepassen.

Tools en Hulpmiddelen

Gelukkig hoef je tegenwoordig niet meer alles handmatig te berekenen. Er zijn tal van tools en hulpmiddelen beschikbaar:

• Rekenmachines: Wetenschappelijke rekenmachines hebben sinus, cosinus en tangens functies.
• Online Calculators: Er zijn veel websites die gespecialiseerde calculators aanbieden voor het berekenen van de schuine zijde. Zoek bijvoorbeeld op "schuine zijde berekenen calculator".
• Apps: Er zijn diverse apps voor smartphones en tablets die je helpen met geometrische berekeningen.
• Meetinstrumenten: Digitale hoekmeters geven nauwkeurige hoekmetingen.

Maak gebruik van deze tools om je berekeningen te controleren en fouten te voorkomen. Ze maken het proces een stuk eenvoudiger en sneller.

Tips voor Nauwkeurigheid

Nauwkeurigheid is cruciaal bij het berekenen van de schuine zijde. Hier zijn een paar tips om fouten te minimaliseren:

• Nauwkeurig Meten: Zorg ervoor dat je de hoek en de bekende zijde zo nauwkeurig mogelijk meet.
• Correcte Eenheden: Gebruik dezelfde eenheden voor alle metingen (bijvoorbeeld meters of centimeters).
• Rond Correct Af: Rond je resultaten pas af aan het einde van de berekening, om afrondingsfouten te voorkomen.
• Dubbelcheck: Controleer je berekeningen altijd, bij voorkeur met een andere methode of calculator.

Onthoud: "Meten is weten, maar controleren is zeker weten!"

Oefening Baart Kunst

Zoals met alles, geldt ook hier: oefening baart kunst. Probeer verschillende scenario's uit, gebruik verschillende hoeken en zijden, en experimenteer met de verschillende trigonometrische functies. Naarmate je meer oefent, zul je steeds meer vertrouwd raken met de principes en de toepassingen.

Start met eenvoudige voorbeelden, zoals het berekenen van de lengte van de schuine zijde van een gelijkzijdige driehoek of een rechthoekige driehoek met bekende hoeken. Naarmate je meer vertrouwen krijgt, kun je overgaan op complexere problemen, zoals het berekenen van de helling van een dak of de lengte van een diagonale steunbalk.

Samenvatting

Het berekenen van de schuine zijde met een hoek is essentieel voor veel praktische toepassingen, van de bouw tot de interieurinrichting. Hoewel het in eerste instantie complex kan lijken, kan het met de juiste tools, kennis en oefening een eenvoudige en bevredigende taak zijn. Onthoud de basisprincipes van trigonometrie (sinus, cosinus, tangens), gebruik online calculators of apps om je te helpen, en neem de tijd om je metingen te controleren.

De Toekomst

De technologie staat niet stil. In de toekomst zullen er waarschijnlijk nog meer geavanceerde tools en technieken beschikbaar komen om de schuine zijde te berekenen. Denk aan augmented reality apps die je helpen bij het meten en visualiseren van constructies, of aan AI-gestuurde systemen die automatisch de optimale hoeken en afmetingen berekenen. Maar de basisprincipes van trigonometrie zullen altijd relevant blijven. Het begrijpen van de wiskunde achter de tools stelt je in staat om ze effectiever te gebruiken.

De wereld om ons heen is vol wiskunde. Door de schuine zijde te begrijpen, krijg je een beter inzicht in de structuren en vormen die ons omringen. Je ziet de wereld met andere ogen, een oog dat niet alleen de lengte en breedte ziet, maar ook de hoeken en verhoudingen.

Wat ga jij nu met deze kennis doen? Ga je een nieuwe schuur bouwen? Een vogelhuisje ontwerpen? Of simpelweg de helling van je dak berekenen? De mogelijkheden zijn eindeloos. De eerste stap is gezet, nu is het tijd om de theorie in de praktijk te brengen.

Waar ga jij de kennis van het berekenen van de schuine zijde voor gebruiken?