Stelling Van Pythagoras Hoek Berekenen
Weet je nog, die ene formule uit de wiskundeles die je nooit echt begreep, maar die je toch moest stampen? De stelling van Pythagoras. Het klinkt misschien als een stoffig stukje theorie, maar geloof me, het is veel relevanter dan je denkt. Vooral als je hoeken wilt berekenen!
Je bent misschien geen wiskundige, maar misschien wel een doe-het-zelver, een architect, een programmeur, of simpelweg iemand die graag dingen begrijpt. In al die gevallen kan de stelling van Pythagoras en het berekenen van hoeken een cruciaal hulpmiddel zijn. Laten we eens duiken in hoe dit werkt en waarom het zo belangrijk is.
Waarom zou je dit willen weten?
Stel je voor:
- Je bouwt een schuurtje in de tuin en wilt zeker weten dat de hoeken precies 90 graden zijn.
- Je ontwerpt een website en moet de positie van elementen nauwkeurig bepalen.
- Je navigeert in de wildernis met een kaart en kompas en moet afstanden en richtingen berekenen.
In al deze scenario's is kennis van de stelling van Pythagoras en het berekenen van hoeken onmisbaar. Het is niet alleen theoretische kennis, maar een praktische vaardigheid die je in talloze situaties van pas kan komen.
De Stelling van Pythagoras: Een Opfrisser
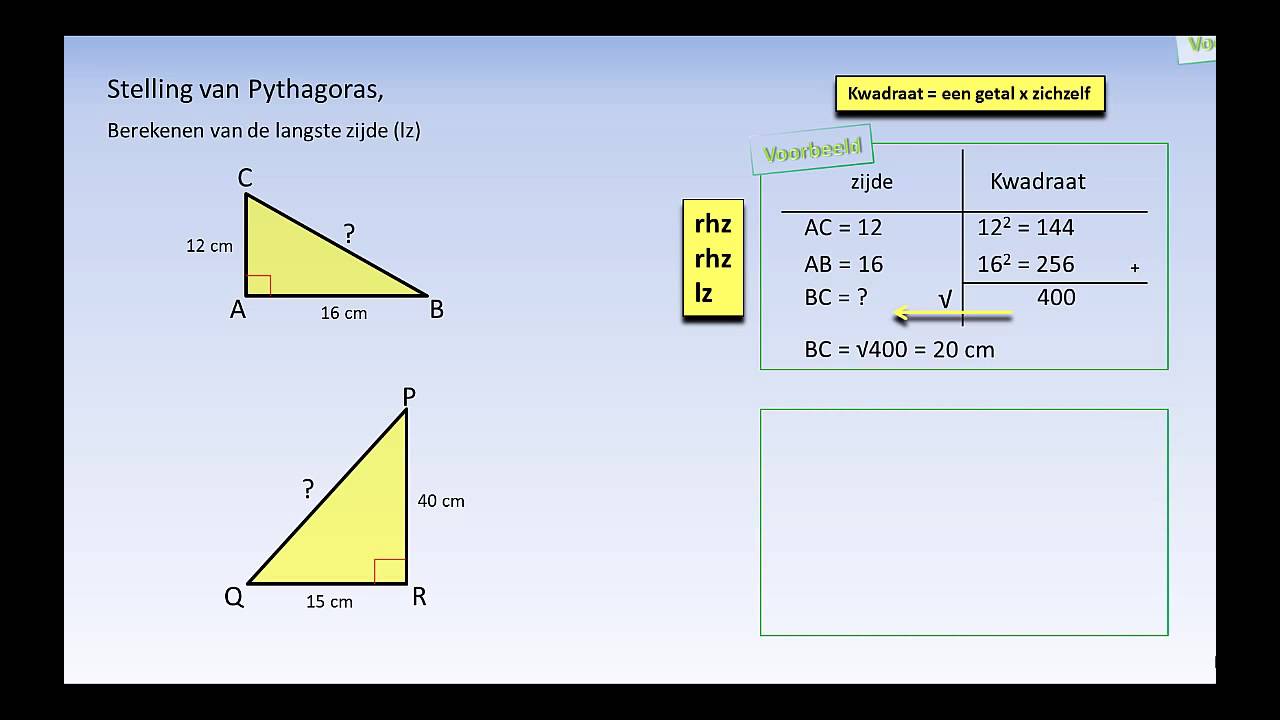
De stelling van Pythagoras is een wiskundige relatie tussen de zijden van een rechthoekige driehoek. Een rechthoekige driehoek is een driehoek met één hoek van 90 graden (een rechte hoek). De stelling stelt:
a2 + b2 = c2
Waar:
- a en b zijn de lengtes van de rechthoekszijden (de zijden die de rechte hoek vormen).
- c is de lengte van de schuine zijde (de zijde tegenover de rechte hoek, ook wel de hypotenusa genoemd).
Simpel gezegd: het kwadraat van de ene rechthoekszijde plus het kwadraat van de andere rechthoekszijde is gelijk aan het kwadraat van de schuine zijde.
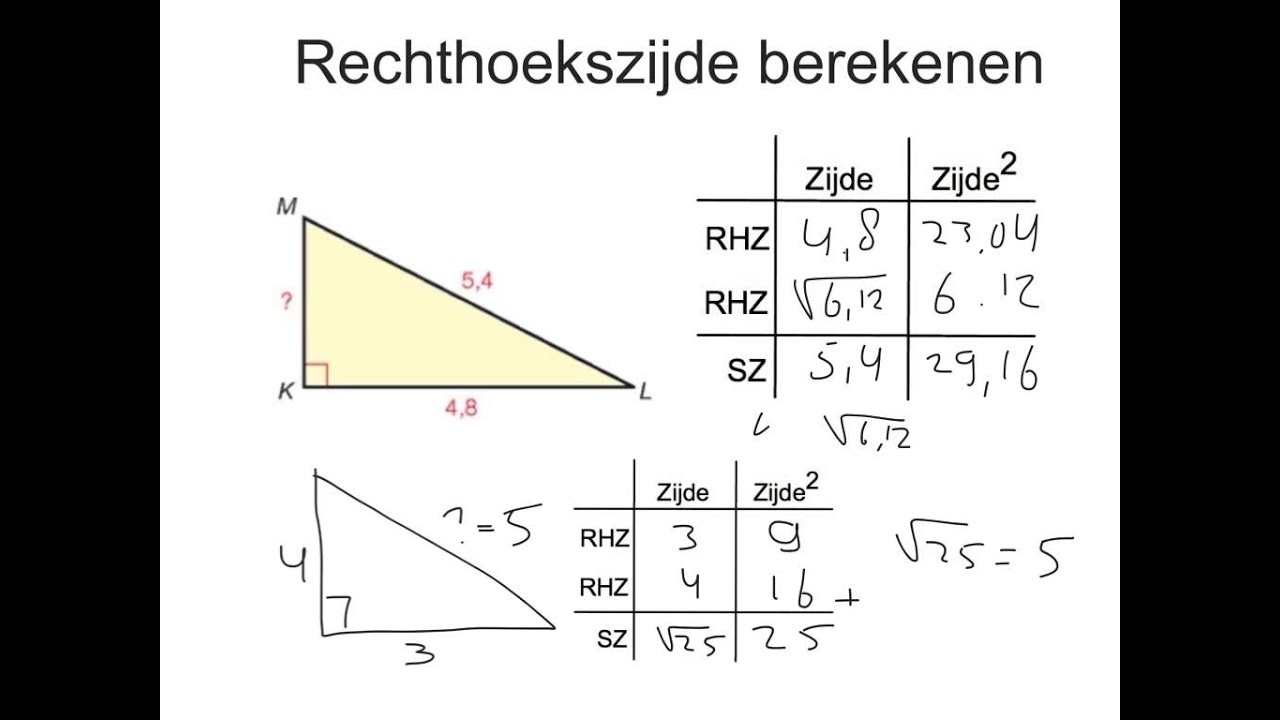
Voorbeeld: Stel a = 3 en b = 4. Dan is c2 = 32 + 42 = 9 + 16 = 25. Dus c = √25 = 5.
Hoeken Berekenen: Meer dan Alleen de Stelling
De stelling van Pythagoras op zichzelf geeft je niet direct de hoeken van een driehoek. Daarvoor hebben we trigonometrie nodig. Trigonometrie is de tak van de wiskunde die zich bezighoudt met de relaties tussen de hoeken en zijden van driehoeken.
De drie belangrijkste trigonometrische functies zijn:
- Sinus (sin): Overstaande zijde / Schuine zijde (sin(hoek) = overstaande / schuine)
- Cosinus (cos): Aanliggende zijde / Schuine zijde (cos(hoek) = aanliggende / schuine)
- Tangens (tan): Overstaande zijde / Aanliggende zijde (tan(hoek) = overstaande / aanliggende)
Om een hoek te berekenen, hebben we de inverse van deze functies nodig. Deze worden ook wel arcsinus (asin of sin-1), arccosinus (acos of cos-1) en arctangens (atan of tan-1) genoemd.
Voorbeeld: Stel we hebben een rechthoekige driehoek met een overstaande zijde van 3 en een aanliggende zijde van 4. Dan is de tangens van de hoek tegenover de overstaande zijde: tan(hoek) = 3/4 = 0.75. De hoek is dan atan(0.75) ≈ 36.87 graden.
Stappenplan voor het Berekenen van een Hoek
- Identificeer de bekende zijden: Welke zijden van de driehoek ken je? De overstaande, aanliggende en/of schuine zijde?
- Kies de juiste trigonometrische functie: Afhankelijk van welke zijden je kent, kies je de sinus, cosinus of tangens.
- Bereken de waarde van de trigonometrische functie: Deel de lengte van de relevante zijden.
- Gebruik de inverse functie: Gebruik arcsinus, arccosinus of arctangens om de hoek te berekenen. De meeste rekenmachines hebben deze functies beschikbaar.
Praktische Toepassingen
Laten we eens kijken naar een paar concrete voorbeelden:
Bouw en Constructie
Zoals eerder genoemd, is het berekenen van hoeken essentieel bij het bouwen van constructies. Denk aan het bepalen van de helling van een dak, het uitzetten van funderingen, of het controleren van de haaksheid van muren. Een kleine afwijking in een hoek kan leiden tot grote problemen in de algehele structuur.
Navigatie
In de navigatie wordt de stelling van Pythagoras en trigonometrie gebruikt om afstanden en richtingen te bepalen. Zowel in de traditionele navigatie met kaart en kompas als in moderne GPS-systemen spelen deze principes een cruciale rol.
Spelontwikkeling en Grafisch Ontwerp
Bij het ontwikkelen van games en grafische ontwerpen is het belangrijk om de positie en oriëntatie van objecten nauwkeurig te bepalen. Trigonometrie wordt gebruikt om objecten te roteren, te verschalen en te positioneren in 2D- en 3D-ruimtes.
Robotica
Robotica is sterk afhankelijk van wiskunde. Voor het berekenen van de hoeken van robotarmen, de positie van sensoren en de trajecten die robots afleggen is de stelling van Pythagoras en het berekenen van hoeken onmisbaar.
Counterpoints: Waarom is dit nog steeds belangrijk?
Je zou kunnen denken: "Met alle moderne technologie, zoals lasers en GPS, is het toch niet meer nodig om deze berekeningen zelf te doen?" Dat is gedeeltelijk waar. Technologie heeft veel taken vereenvoudigd. Echter, het begrijpen van de onderliggende principes is nog steeds belangrijk:
- Foutopsporing: Als je de basisprincipes begrijpt, kun je fouten in de output van technologie sneller herkennen en corrigeren.
- Creativiteit en Innovatie: Kennis van de wiskunde achter technologie stelt je in staat om creatieve oplossingen te bedenken en nieuwe technologieën te ontwikkelen.
- Onafhankelijkheid: Je bent niet volledig afhankelijk van technologie. Als de technologie faalt, kun je nog steeds de basisberekeningen zelf uitvoeren.
Tools en Hulpmiddelen
Gelukkig zijn er tegenwoordig veel tools en hulpmiddelen beschikbaar om je te helpen met het berekenen van hoeken en het toepassen van de stelling van Pythagoras:
- Rekenmachines: De meeste wetenschappelijke rekenmachines hebben trigonometrische functies en inverse functies.
- Online rekenhulpen: Er zijn veel websites en apps die je helpen met het berekenen van hoeken en zijden van driehoeken.
- Software: Programma's zoals GeoGebra zijn uitstekend geschikt voor het visualiseren van meetkundige problemen en het uitvoeren van berekeningen.
- Cursussen en tutorials: Online platforms zoals Khan Academy bieden gratis cursussen over trigonometrie en gerelateerde onderwerpen.
Oefening Baart Kunst
De beste manier om de stelling van Pythagoras en het berekenen van hoeken onder de knie te krijgen, is door te oefenen. Begin met eenvoudige voorbeelden en werk geleidelijk toe naar complexere problemen.
Hier zijn een paar oefensuggesties:
- Bepaal de lengte van de schuine zijde van een rechthoekige driehoek als je de lengtes van de rechthoekszijden weet.
- Bepaal de grootte van een hoek in een rechthoekige driehoek als je de lengtes van twee zijden weet.
- Pas de stelling van Pythagoras toe op een praktisch probleem, zoals het berekenen van de lengte van een ladder die tegen een muur staat.
Vergeet niet, het is oké om fouten te maken. Het belangrijkste is dat je leert van je fouten en blijft oefenen.
Conclusie: Meer dan een Formule
De stelling van Pythagoras en het berekenen van hoeken is meer dan alleen een formule. Het is een krachtig hulpmiddel dat je kan helpen om de wereld om je heen beter te begrijpen en problemen op te lossen in verschillende vakgebieden.
Door de basisprincipes te begrijpen en te oefenen, kun je deze vaardigheden toepassen in je dagelijks leven en je professionele carrière.
Dus, waar ga jij de stelling van Pythagoras en het berekenen van hoeken voor gebruiken? Ga je nu een hoek in je huis opmeten of berekenen?
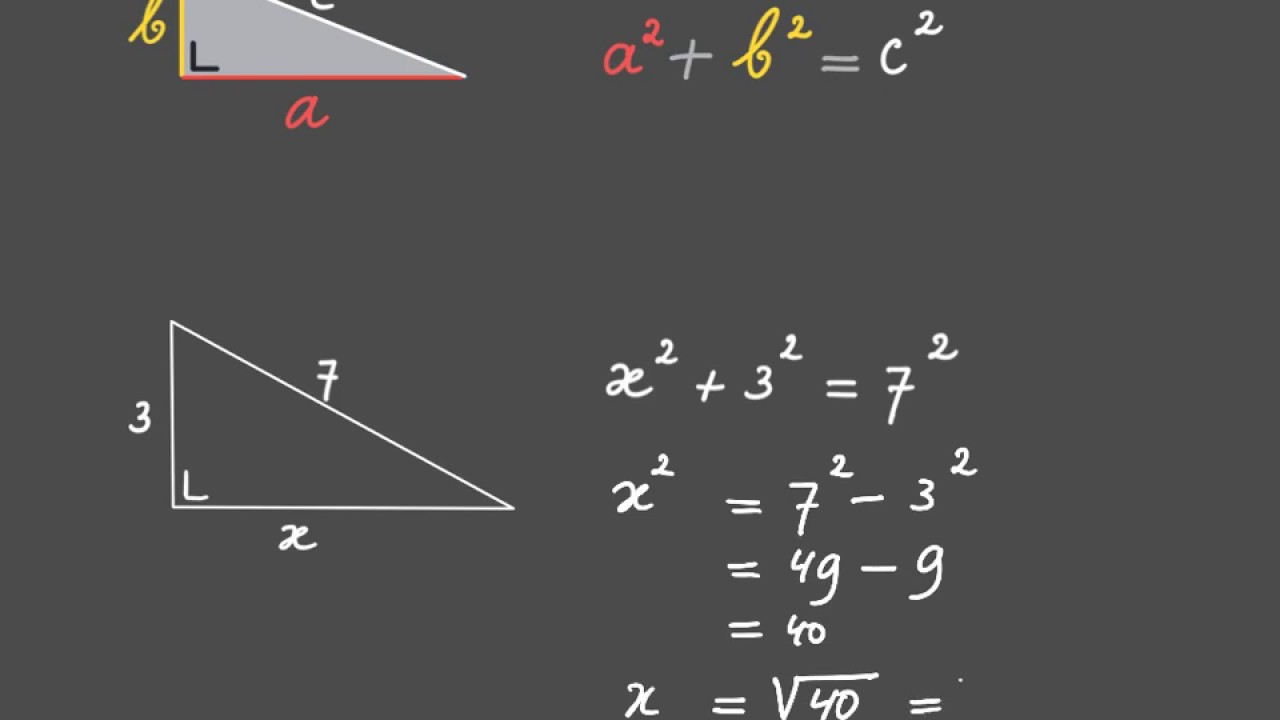
Bekijk ook deze gerelateerde berichten:
- Bloedonderzoek Alat Wat Is Dat
- Hoeveel Slaap Baby 1 Jaar
- Hoeveel Procent Gaat Er Van Je Bruto Salaris Af
- Hoe Bereken Je 1 Procent
- Het Land Van Ooit Zwarte Ridder
- Hoeveel Geld Is Een Rug
- Wat Valt Onder Regio Midden
- Wat Is De Aanleiding Van De Eerste Wereldoorlog
- Geschiedenis Examen Vmbo Tl 2023
- Hoe Krijg Je De Pest
