Stelling Van Pythagoras Rechte Zijde Berekenen

Ken je dat moment dat je naar een schuine ladder kijkt, leunend tegen een muur, en je je afvraagt: hoe hoog reikt die ladder eigenlijk? Of dat je een perfect recht hoekje in je tuin wilt aanleggen, maar geen idee hebt hoe je de juiste afmetingen moet bepalen? Je bent niet de enige! Veel mensen worstelen met dit soort vragen, en de oplossing ligt verrassend genoeg in een eeuwenoude wiskundige formule: de Stelling van Pythagoras.

Deze stelling, vernoemd naar de Griekse wiskundige Pythagoras, is veel meer dan een abstracte formule. Het is een krachtig hulpmiddel dat ons helpt afstanden te berekenen, hoeken te bepalen, en problemen op te lossen in talloze alledaagse situaties. Maar laten we eerlijk zijn, wiskunde kan soms intimiderend zijn. Daarom gaan we deze complexe ideeën stap voor stap ontleden, zodat je straks zelfverzekerd met de Stelling van Pythagoras aan de slag kunt. Geen moeilijke formules meer, maar praktische toepassingen en een helder begrip.

Wat is de Stelling van Pythagoras precies?

De Stelling van Pythagoras is een fundamentele regel in de meetkunde die de relatie beschrijft tussen de zijden van een rechthoekige driehoek. Een rechthoekige driehoek is een driehoek met één hoek van precies 90 graden, ook wel een rechte hoek genoemd. De zijde tegenover de rechte hoek noemen we de hypotenusa, en de twee andere zijden noemen we de rechthoekszijden (ook wel catheti).

De stelling zelf is verrassend eenvoudig: de som van de kwadraten van de lengtes van de rechthoekszijden is gelijk aan het kwadraat van de lengte van de hypotenusa. In formulevorm:

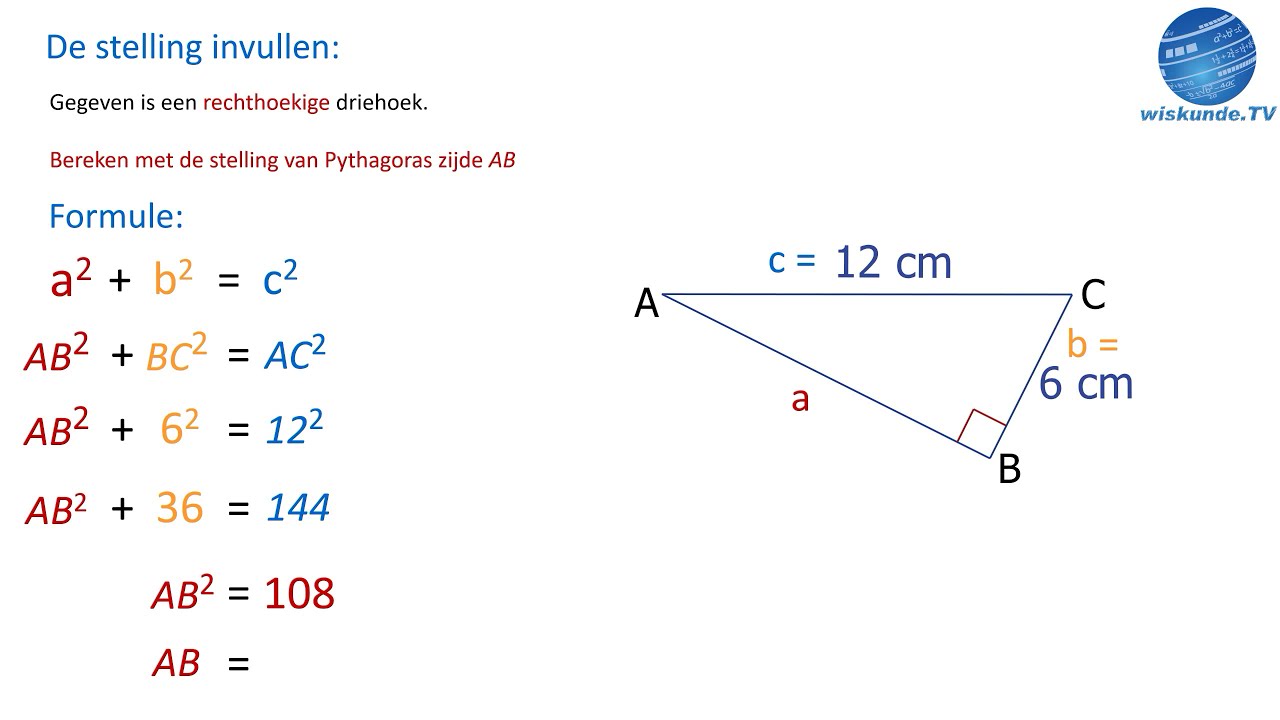
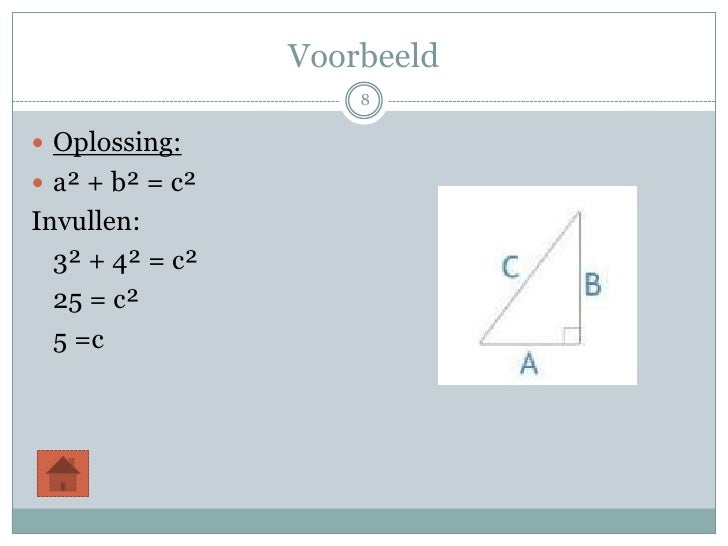
a² + b² = c²

Waar:

• a en b de lengtes zijn van de rechthoekszijden.
• c de lengte is van de hypotenusa.

Dus, als je de lengte van twee zijden van een rechthoekige driehoek weet, kun je de lengte van de derde zijde berekenen. En dat is waar de magie begint!

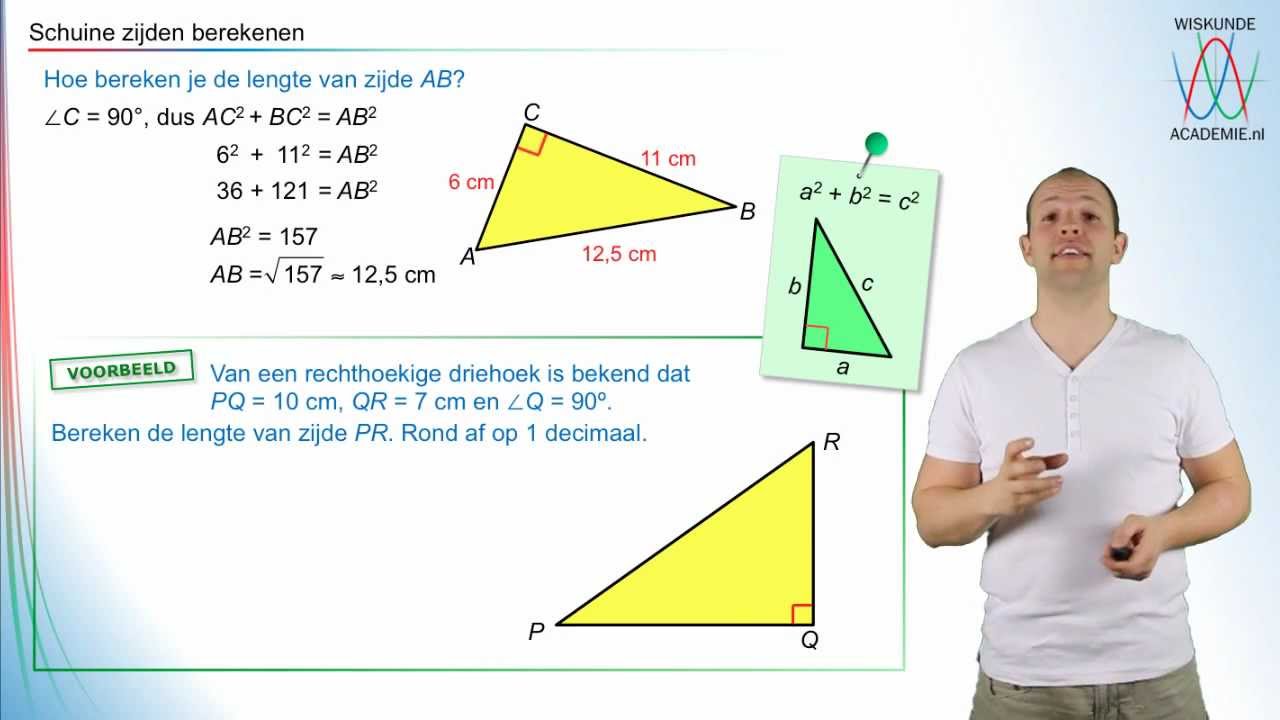
Hoe bereken je een rechthoekszijde?

Vaak weet je de lengte van de hypotenusa en één rechthoekszijde, en wil je de lengte van de andere rechthoekszijde berekenen. Geen probleem! We kunnen de formule eenvoudig aanpassen.

Stel, je weet de lengte van de hypotenusa (c) en de lengte van rechthoekszijde a. Je wilt rechthoekszijde b berekenen. Dan ziet de formule er als volgt uit:

b² = c² - a²

Om b te vinden, neem je de wortel van het resultaat:

b = √(c² - a²)

Hetzelfde geldt als je de lengte van de hypotenusa (c) en de lengte van rechthoekszijde b weet, en je wilt rechthoekszijde a berekenen. Dan ziet de formule er als volgt uit:

a² = c² - b²

Om a te vinden, neem je de wortel van het resultaat:

a = √(c² - b²)

Een praktisch voorbeeld

Stel, je hebt een ladder van 5 meter (de hypotenusa) die tegen een muur staat. De voet van de ladder staat 3 meter van de muur (een rechthoekszijde). Hoe hoog reikt de ladder tegen de muur (de andere rechthoekszijde)?

1. c (hypotenusa) = 5 meter
2. a (rechthoekszijde) = 3 meter
3. We willen b (de hoogte tegen de muur) berekenen.

Gebruik de formule: b = √(c² - a²)

b = √(5² - 3²)

b = √(25 - 9)

b = √16

b = 4 meter

De ladder reikt dus 4 meter hoog tegen de muur.

Waarom is de Stelling van Pythagoras belangrijk?

De Stelling van Pythagoras is niet alleen relevant voor schoolboeken en wiskundeleraren. Het is een fundamenteel principe dat wordt gebruikt in verschillende velden, waaronder:

• Architectuur en constructie: Voor het berekenen van afstanden, hoeken en de stabiliteit van gebouwen. Denk aan het ontwerpen van schuine daken, het plaatsen van funderingen en het bepalen van de juiste afmetingen voor constructies.
• Navigatie: Voor het bepalen van de kortste route tussen twee punten, vooral in de luchtvaart en scheepvaart. GPS-systemen gebruiken triangulatie, een techniek gebaseerd op de Stelling van Pythagoras, om je positie te bepalen.
• Engineering: Voor het ontwerpen van machines, bruggen en andere structuren. Het berekenen van krachten en spanningen vereist vaak het gebruik van de Stelling van Pythagoras.
• Tuinieren en landschapsarchitectuur: Voor het uitzetten van rechte hoeken, het berekenen van de benodigde materialen en het ontwerpen van terrassen en paden.
• Gaming en 3D-modellering: Voor het berekenen van afstanden en hoeken in virtuele werelden, wat essentieel is voor realistische bewegingen en perspectieven.

Kortom, de Stelling van Pythagoras is een krachtig hulpmiddel dat ons helpt de wereld om ons heen te begrijpen en problemen op te lossen.

Counterpoints en Misvattingen

Sommige mensen beschouwen de Stelling van Pythagoras als een abstracte en nutteloze theorie. Ze vragen zich af waarom ze dit ooit in hun leven nodig zouden hebben. Het is waar dat je de formule misschien niet dagelijks gebruikt, maar het onderliggende principe van het berekenen van afstanden en hoeken is van onschatbare waarde in vele situaties.

Een andere misvatting is dat de Stelling van Pythagoras alleen van toepassing is op perfecte rechthoekige driehoeken. In de praktijk komen perfecte rechthoeken zelden voor. Echter, de Stelling van Pythagoras kan ook worden gebruikt om benaderingen te maken in situaties waarin geen perfecte rechthoek aanwezig is. Door de situatie te vereenvoudigen en te modelleren als een rechthoekige driehoek, kun je een redelijke schatting krijgen.

Bovendien, het leren van de Stelling van Pythagoras bevordert het logisch denken en probleemoplossende vaardigheden, wat ook buiten de wiskunde van pas komt.

Hoe kun je de Stelling van Pythagoras beter begrijpen?

Hier zijn enkele tips om de Stelling van Pythagoras beter te begrijpen en toe te passen:

• Visualiseer: Teken rechthoekige driehoeken en label de zijden. Gebruik verschillende lengtes en oefen met het berekenen van de ontbrekende zijde.
• Praktijk: Zoek voorbeelden in je omgeving waar je de Stelling van Pythagoras kunt toepassen. Meet bijvoorbeeld de lengte en breedte van een rechthoekige tafel en bereken de lengte van de diagonaal.
• Gebruik online tools: Er zijn veel online calculators en interactieve tools beschikbaar die je kunnen helpen bij het berekenen van de zijden van een rechthoekige driehoek en het visualiseren van de Stelling van Pythagoras.
• Zoek uitleg in verschillende vormen: Lees artikelen, bekijk video's en luister naar podcasts over de Stelling van Pythagoras. Verschillende bronnen kunnen je helpen de concepten op verschillende manieren te begrijpen.
• Vraag om hulp: Als je vastloopt, aarzel dan niet om hulp te vragen aan een wiskundeleraar, een vriend of een online forum.

Onthoud dat oefening kunst baart. Hoe meer je oefent met het toepassen van de Stelling van Pythagoras, hoe beter je het zult begrijpen en hoe zelfverzekerder je zult zijn in het gebruik ervan.

Oplossingsgerichte aanpak

In plaats van alleen te focussen op de theorie, is het belangrijk om te kijken naar praktische toepassingen en oplossingen. Bijvoorbeeld:

• Online tools: Gebruik websites en apps die de berekeningen voor je doen, zodat je je kunt concentreren op het begrijpen van het concept en het toepassen ervan in de praktijk.
• Stapsgewijze handleidingen: Volg stapsgewijze handleidingen die je door verschillende scenario's leiden en je laten zien hoe je de Stelling van Pythagoras kunt gebruiken om problemen op te lossen.
• Real-world projecten: Werk aan real-world projecten, zoals het bouwen van een vogelhuisje of het ontwerpen van een kleine tuin, waarbij je de Stelling van Pythagoras moet toepassen om de juiste afmetingen te bepalen.

Door een oplossingsgerichte aanpak te hanteren, kun je de Stelling van Pythagoras niet alleen beter begrijpen, maar ook leren hoe je het effectief kunt gebruiken om problemen in je dagelijks leven op te lossen.

De Stelling van Pythagoras is een krachtige tool die je kan helpen om problemen op te lossen in veel verschillende situaties. Door de formule te begrijpen, te visualiseren en te oefenen met praktische voorbeelden, kun je je wiskundige vaardigheden verbeteren en je zelfvertrouwen vergroten. Dus, pak een pen en papier, zoek een paar rechthoekige driehoeken en begin met oefenen!

Nu je meer weet over de Stelling van Pythagoras, waar ga jij deze kennis voor gebruiken?