Wat Is De Abc Formule

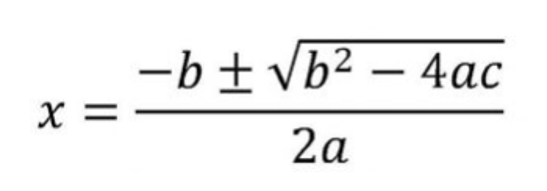
De ABC-formule, ook wel bekend als de wortelformule of de kwadratische formule, is een essentieel instrument in de wiskunde, met name bij het oplossen van kwadratische vergelijkingen. Hoewel de formule misschien intimiderend lijkt, is het begrijpen ervan cruciaal voor het beheersen van algebra en calculus. Dit artikel zal de ABC-formule in detail ontleden, de afleiding ervan uitleggen, de toepassingen ervan illustreren en enkele veelvoorkomende valkuilen vermijden.

Wat is een Kwadratische Vergelijking?

Voordat we de ABC-formule zelf induiken, is het belangrijk om te begrijpen wat een kwadratische vergelijking is. Een kwadratische vergelijking is een polynoomvergelijking van de tweede graad, die algemeen kan worden weergegeven als:

ax² + bx + c = 0

waarbij a, b en c constanten zijn, en a ≠ 0. De term 'kwadratisch' verwijst naar de hoogste macht van de variabele x, die 2 is. Het doel is om de waarde(n) van x te vinden die de vergelijking waar maken. Deze waarden worden de wortels, oplossingen of nulpunten van de kwadratische vergelijking genoemd.

De ABC-Formule: De Sleutel tot Oplossing

De ABC-formule biedt een directe manier om de wortels van een kwadratische vergelijking te vinden, ongeacht hoe complex of eenvoudig deze is. De formule luidt:

x = (-b ± √(b² - 4ac)) / 2a

Deze formule geeft twee mogelijke oplossingen voor x, aangeduid met het ±-teken. Eén oplossing wordt verkregen door de plus te gebruiken en de andere door de min te gebruiken. Het deel onder het wortelteken, b² - 4ac, wordt de discriminant genoemd en speelt een cruciale rol bij het bepalen van de aard van de wortels.

De Discriminant: Het Hart van de Aard van de Wortels

De discriminant, Δ = b² - 4ac, geeft informatie over het aantal en de aard van de wortels van de kwadratische vergelijking:

• Δ > 0: De vergelijking heeft twee verschillende reële wortels. Dit betekent dat de grafiek van de kwadratische functie de x-as op twee verschillende punten snijdt.
• Δ = 0: De vergelijking heeft precies één reële wortel (een dubbele wortel). In dit geval raakt de grafiek van de kwadratische functie de x-as op één punt.
• Δ < 0: De vergelijking heeft geen reële wortels, maar twee complexe wortels (conjugaten). De grafiek van de kwadratische functie snijdt de x-as niet.

Hoe de ABC-Formule te Gebruiken: Stap voor Stap

Hier volgt een stapsgewijze handleiding voor het toepassen van de ABC-formule:

1. Identificeer a, b en c: Zorg ervoor dat de kwadratische vergelijking in de standaardvorm staat (ax² + bx + c = 0) en noteer de waarden van a, b en c.
2. Bereken de Discriminant: Bereken Δ = b² - 4ac. Dit helpt je om de aard van de wortels te begrijpen.
3. Pas de ABC-formule toe: Vervang de waarden van a, b en c in de formule: x = (-b ± √(b² - 4ac)) / 2a.
4. Vereenvoudig de uitdrukking: Vereenvoudig de uitdrukking zoveel mogelijk. Let op de volgorde van de bewerkingen (eerst de wortel, dan de vermenigvuldiging, dan de optelling/aftrekking).
5. Bereken de wortels: Bereken de twee mogelijke waarden van x met behulp van zowel de plus als de min in de ±.

Voorbeelden uit de Praktijk

Laten we enkele voorbeelden bekijken om het gebruik van de ABC-formule te illustreren:

Voorbeeld 1: Twee verschillende reële wortels

Los de volgende vergelijking op: x² + 5x + 6 = 0

1. a = 1, b = 5, c = 6
2. Δ = 5² - 4 * 1 * 6 = 25 - 24 = 1 (Δ > 0, dus twee reële wortels)
3. x = (-5 ± √1) / (2 * 1)
4. x = (-5 ± 1) / 2
5. x₁ = (-5 + 1) / 2 = -2 en x₂ = (-5 - 1) / 2 = -3

De oplossingen zijn x = -2 en x = -3.

Voorbeeld 2: Eén reële wortel (dubbele wortel)

Los de volgende vergelijking op: x² - 4x + 4 = 0

1. a = 1, b = -4, c = 4
2. Δ = (-4)² - 4 * 1 * 4 = 16 - 16 = 0 (Δ = 0, dus één reële wortel)
3. x = (4 ± √0) / (2 * 1)
4. x = 4 / 2 = 2

De oplossing is x = 2 (een dubbele wortel).

Voorbeeld 3: Geen reële wortels (complexe wortels)

Los de volgende vergelijking op: x² + 2x + 5 = 0

1. a = 1, b = 2, c = 5
2. Δ = 2² - 4 * 1 * 5 = 4 - 20 = -16 (Δ < 0, dus geen reële wortels)
3. x = (-2 ± √-16) / (2 * 1)
4. x = (-2 ± 4i) / 2 (waarbij i de imaginaire eenheid is, √-1)
5. x₁ = -1 + 2i en x₂ = -1 - 2i

De oplossingen zijn de complexe getallen x = -1 + 2i en x = -1 - 2i.

Reële Toepassingen van Kwadratische Vergelijkingen en de ABC-Formule

Kadratische vergelijkingen en de ABC-formule vinden toepassingen in diverse velden, waaronder:

• Natuurkunde: Het berekenen van de baan van een projectiel, de hoogte van een object dat in de lucht wordt gegooid, en de beweging van objecten onder invloed van de zwaartekracht.
• Engineering: Het ontwerpen van bruggen, gebouwen en andere structuren, waarbij krachten en belastingen worden geanalyseerd.
• Financiën: Het berekenen van samengestelde rente, het modelleren van investeringen en het voorspellen van marktontwikkelingen.
• Computerwetenschappen: Het optimaliseren van algoritmen, het ontwerpen van grafische interfaces en het modelleren van complexe systemen.
• Economie: Het modelleren van vraag- en aanbodcurves, het analyseren van marktevenwichten en het voorspellen van economische groei.

Denk bijvoorbeeld aan een voetballer die een bal trapt. De baan van de bal kan worden gemodelleerd met een kwadratische vergelijking. Met behulp van de ABC-formule kunnen we de afstand bepalen die de bal zal afleggen voordat hij landt, of de maximale hoogte die hij zal bereiken.

Of neem een ingenieur die een brug ontwerpt. De spanning en belasting op de brug kunnen worden gemodelleerd met behulp van kwadratische vergelijkingen. Door de ABC-formule te gebruiken, kan de ingenieur bepalen hoe de brug moet worden ontworpen om veilig en stabiel te zijn.

Veelvoorkomende Fouten om te Vermijden

Bij het gebruik van de ABC-formule zijn er enkele veelvoorkomende fouten die je moet vermijden:

• Verkeerde identificatie van a, b en c: Zorg ervoor dat de vergelijking in de standaardvorm staat voordat je de coëfficiënten identificeert.
• Verkeerde berekening van de discriminant: Let op de volgorde van de bewerkingen en controleer je berekeningen zorgvuldig.
• Tekenfouten: Wees extra voorzichtig met de tekens van a, b en c, vooral als ze negatief zijn.
• Verkeerde vereenvoudiging: Vereenvoudig de uitdrukking stap voor stap en let op de wiskundige regels.
• Het vergeten van beide oplossingen: Vergeet niet dat de ABC-formule twee mogelijke oplossingen geeft, één met de plus en één met de min.

Conclusie: Beheers de ABC-Formule

De ABC-formule is een krachtig hulpmiddel voor het oplossen van kwadratische vergelijkingen en het begrijpen van de aard van hun wortels. Door de stappen zorgvuldig te volgen, de discriminant te begrijpen en veelvoorkomende fouten te vermijden, kun je deze formule met succes toepassen in een breed scala aan wiskundige en real-world problemen. Oefening baart kunst! Blijf oefenen met verschillende soorten kwadratische vergelijkingen om je vaardigheden te verbeteren en je vertrouwen in de ABC-formule te vergroten.

Neem de tijd om de concepten te herhalen, los extra oefenopgaven op en raadpleeg bronnen zoals wiskundeboeken, online tutorials of docenten om je begrip van de ABC-formule te verdiepen. Met de juiste inspanning en toewijding kun je deze essentiële wiskundige tool beheersen en je succes in de wiskunde vergroten.