Wat Is De Basis Van Een Driehoek

Heb je ooit naar een dak gekeken, een stuk pizza gepakt, of zelfs een verkeersbord bestudeerd? Dan ben je al in aanraking gekomen met de basis van een driehoek, misschien zonder er bewust van te zijn. In de wiskunde, en in het dagelijks leven, speelt de driehoek een cruciale rol. Maar wat is nu precies die basis, en waarom is het zo belangrijk om dit concept te begrijpen?

Laten we eerlijk zijn, wiskunde kan soms intimiderend zijn. Al die termen, formules en regels... het kan je behoorlijk overweldigen. Maar het is belangrijk om te onthouden dat wiskunde niet zomaar abstracte theorie is. Het is een gereedschap dat ons helpt de wereld om ons heen te begrijpen en te voorspellen. De basis van een driehoek is een van die fundamentele bouwstenen die je kunt gebruiken om complexe problemen op te lossen en de structuren om je heen te waarderen. Laten we samen duiken in dit onderwerp en ontdekken hoe verrassend nuttig het kan zijn.

De Definitie van de Basis van een Driehoek

In de eenvoudigste bewoordingen is de basis van een driehoek gewoon een van de zijden van de driehoek. Het is echter niet zo willekeurig als het klinkt. In de context van het berekenen van de oppervlakte van een driehoek, wordt de basis vaak beschouwd als de zijde waarnaar de hoogte (de loodrechte afstand van de basis naar het tegenoverliggende hoekpunt) wordt gemeten. Denk eraan als de "vloer" waarop de driehoek rust, hoewel dit visuele hulpmiddel niet altijd letterlijk hoeft te kloppen.

Het is belangrijk om te onthouden dat elke zijde van een driehoek in principe als basis kan worden beschouwd. De keuze van de basis is vaak afhankelijk van de beschikbare informatie of het doel van de berekening. Als je bijvoorbeeld de hoogte al kent ten opzichte van een specifieke zijde, dan is het logisch om die zijde als basis te kiezen.

Verschillende Soorten Driehoeken en hun Basis

De eigenschappen van de basis kunnen variëren afhankelijk van het type driehoek:

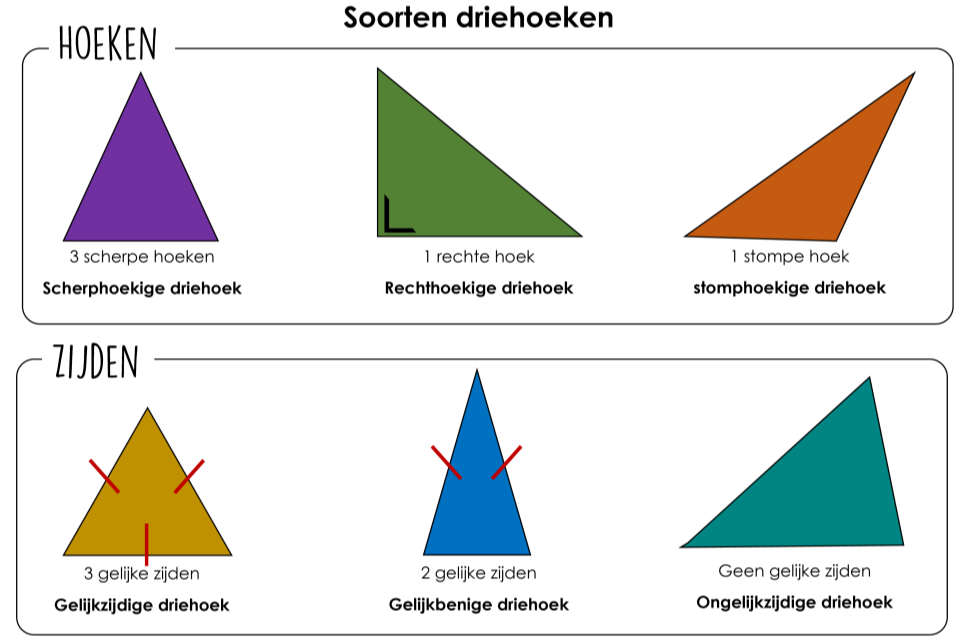
Gelijkzijdige Driehoek: In een gelijkzijdige driehoek zijn alle drie de zijden even lang. Daarom kan elke zijde als basis worden beschouwd, zonder dat dit de berekeningen beïnvloedt.
Gelijkbenige Driehoek: Een gelijkbenige driehoek heeft twee zijden die even lang zijn. De derde zijde, die niet even lang is als de andere twee, wordt vaak als de basis beschouwd. De gelijke zijden heten de benen.
Ongelijkzijdige Driehoek: In een ongelijkzijdige driehoek zijn alle drie de zijden van verschillende lengtes. Ook hier kan elke zijde als basis worden gekozen, afhankelijk van de context.
Rechthoekige Driehoek: Een rechthoekige driehoek heeft een hoek van 90 graden. De twee zijden die de rechte hoek vormen, worden de rechthoekszijden genoemd. Een van deze rechthoekszijden kan als basis worden beschouwd, waarbij de andere rechthoekszijde dan de hoogte is. De zijde tegenover de rechte hoek is de hypotenusa.

Waarom is de Basis Belangrijk?

De basis van een driehoek is niet zomaar een willekeurige zijde. Het is een essentieel element bij het bepalen van verschillende eigenschappen, zoals de oppervlakte.

Oppervlakteberekening: De meest voorkomende toepassing van de basis is bij de berekening van de oppervlakte van een driehoek. De formule hiervoor is:

Oppervlakte = (1/2) * basis * hoogte

Zoals je kunt zien, is de lengte van de basis direct van invloed op de berekende oppervlakte. Zonder de basis (en de bijbehorende hoogte) is het onmogelijk om de oppervlakte van een driehoek te bepalen.

Stabiliteit en Structuur: Driehoeken worden veel gebruikt in de architectuur en de techniek vanwege hun stabiliteit. De basis is cruciaal voor het verdelen van de krachten en het garanderen van de structurele integriteit. Denk aan de basis van een brugpijler of de constructie van een dak.

Real-World Impact: Meer dan alleen een wiskundeles

De principes van driehoeken, en dus ook het concept van de basis, vinden we overal om ons heen. Denk aan:

Architectuur: Bruggen, daken, torens - veel constructies maken gebruik van driehoeken voor stabiliteit en stevigheid. De basis is essentieel voor het berekenen van de benodigde materialen en het garanderen van de veiligheid.
Navigatie: In de navigatie, bijvoorbeeld bij het bepalen van afstanden met behulp van triangulatie, spelen driehoeken een cruciale rol. De basislijnen worden gebruikt om hoeken te meten en posities te bepalen.
Grafisch Ontwerp: Driehoeken worden veel gebruikt in grafische ontwerpen voor visuele compositie en het creëren van dynamische effecten. De basis kan worden gebruikt om de verhoudingen en de balans in een ontwerp te bepalen.
Games en Animatie: In computer graphics worden 3D-modellen vaak opgebouwd uit kleine driehoeken (polygonen). De basis en hoogte van deze driehoeken bepalen de vorm en textuur van de objecten.

Een concreet voorbeeld: stel je voor dat je een zeilboot ontwerpt. De vorm van het zeil, vaak een driehoek, is cruciaal voor de prestaties van de boot. De lengte van de basis van het zeil, samen met de hoogte, bepaalt het oppervlak en dus de hoeveelheid wind die het zeil kan vangen. Een onjuiste berekening van de basis kan leiden tot een inefficiënt zeil en een slechte performance van de boot.

Counterpoints: Is de Basis Echt Zo Belangrijk?

Sommigen beweren misschien dat in de geavanceerde wiskunde, met complexe geometrische vormen, de simpele definitie van de basis van een driehoek minder relevant wordt. En dat is tot op zekere hoogte waar. In de hogere wiskunde zijn er meer abstracte concepten en generalisaties die de rol van de "basis" overnemen. Echter, het fundamentele begrip van de basis als een referentiepunt voor hoogte en oppervlakte blijft essentieel voor het begrijpen van deze meer geavanceerde concepten.

Een ander argument kan zijn dat moderne software de berekeningen automatisch uitvoert, waardoor het handmatig bepalen van de basis minder belangrijk wordt. Hoewel dit waar is, vereist het gebruik van deze software nog steeds een fundamenteel begrip van de principes die eraan ten grondslag liggen. Zonder dit begrip is het moeilijk om de resultaten te interpreteren en kritisch te beoordelen.

Oplossingsgericht: De Basis Als Fundament voor Verder Leren

Het begrijpen van de basis van een driehoek is meer dan alleen een wiskundeles; het is een springplank naar het begrijpen van meer complexe concepten. Hier zijn een paar ideeën om je begrip verder te verdiepen:

Oefen met verschillende soorten driehoeken: Bereken de oppervlakte van verschillende driehoeken, waarbij je verschillende zijden als basis kiest. Experimenteer met verschillende hoogtes en kijk hoe dit de oppervlakte beïnvloedt.
Visualiseer de concepten: Gebruik geometrische software of online tools om driehoeken te tekenen en te manipuleren. Dit kan je helpen om de relatie tussen de basis, de hoogte en de oppervlakte beter te begrijpen.
Zoek naar toepassingen in de echte wereld: Ga op zoek naar voorbeelden van driehoeken in je omgeving. Analyseer hoe de basis en de hoogte worden gebruikt in deze toepassingen.
Verdiep je in trigonometrie: Trigonometrie is de studie van de relaties tussen de zijden en hoeken van driehoeken. Dit is een vervolgstap die je kan helpen om nog complexere problemen op te lossen.

Denk aan de basis van een driehoek als de eerste noot van een melodie. Het is eenvoudig, maar cruciaal voor het opbouwen van een complex en harmonieus geheel. Beheers deze basis en je zult versteld staan van de mogelijkheden die zich openen.

Conclusie

De basis van een driehoek, zo simpel als het lijkt, is een fundamenteel concept met een breed scala aan toepassingen. Van het berekenen van de oppervlakte tot het ontwerpen van stabiele structuren, de basis speelt een essentiële rol. Door dit concept te begrijpen, leg je een sterke basis voor verder leren in de wiskunde en daarbuiten.

Nu je dit artikel hebt gelezen, wat is jouw volgende stap om je begrip van de basis van een driehoek verder te verdiepen? Ga je oefenen met berekeningen, op zoek naar toepassingen in de echte wereld, of misschien zelfs verder duiken in de wereld van de trigonometrie?