Wat Is De Noemer En Wat Is De Teller

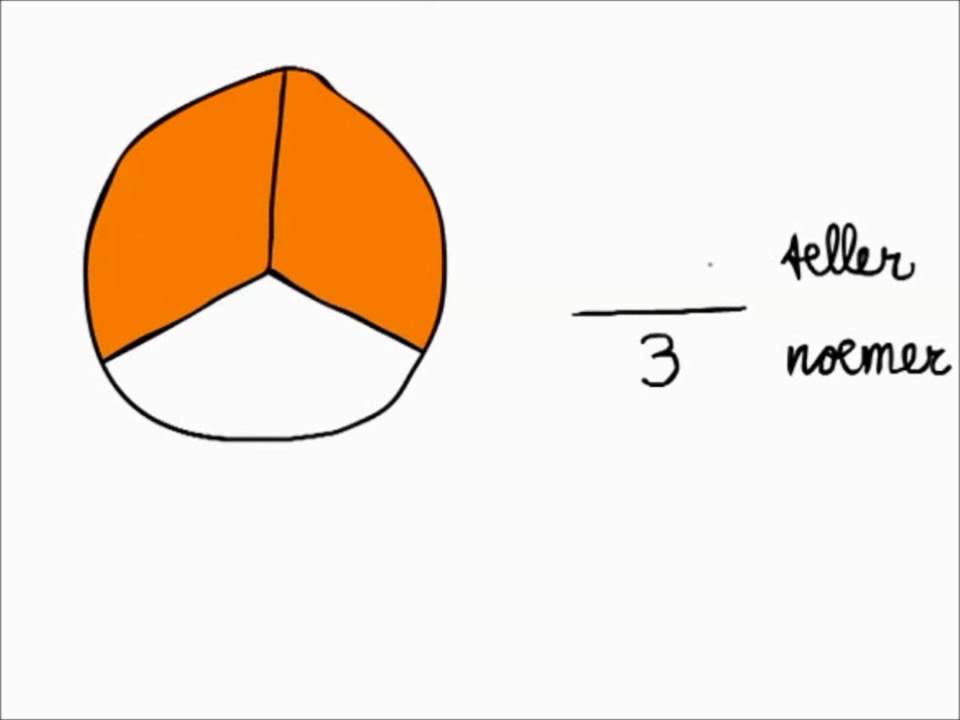
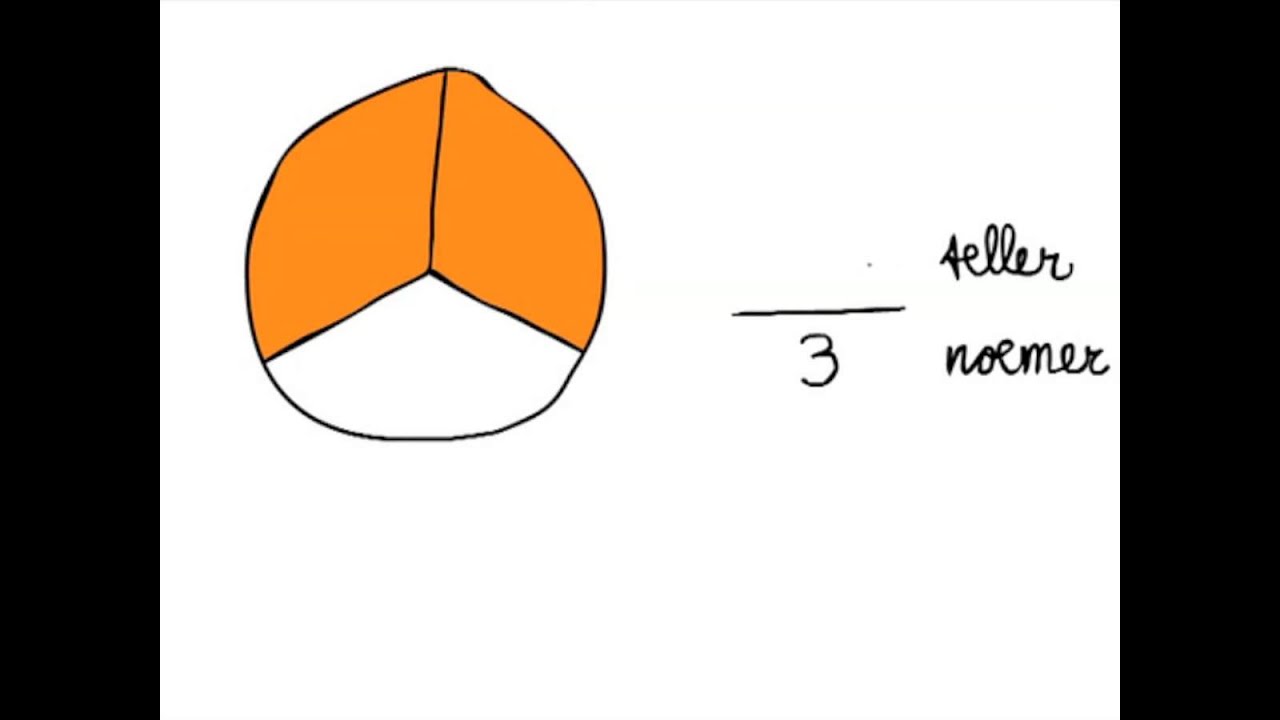
Heb je je ooit afgevraagd wat die twee getallen boven en onder een streep betekenen? We duiken vandaag in de wereld van breuken en ontrafelen de mysteries van de teller en de noemer. Dit artikel is speciaal geschreven voor iedereen die breuken beter wil begrijpen, of je nu een scholier bent, een ouder die huiswerk helpt, of gewoon je wiskundige kennis wilt opfrissen.

Wat is een Breuk Eigenlijk?

Een breuk is een manier om een deel van een geheel weer te geven. Stel je voor dat je een pizza hebt. Als je die pizza in 8 gelijke stukken snijdt en je neemt er 3 stukken van, dan heb je 3/8 van de pizza. Die 3/8 is een breuk.

Maar wat betekenen die getallen precies?

De Teller: Het Aantal Geselecteerde Delen

De teller is het getal dat boven de breukstreep staat. Het vertelt ons hoeveel delen we hebben geselecteerd of in beschouwing nemen. In het voorbeeld van de pizza is de teller 3. Dit betekent dat we 3 van de 8 stukken hebben.

De teller geeft aan hoeveel 'eenheden' van de noemer we hebben.
Het is belangrijk om te onthouden dat de teller kleiner, gelijk aan, of groter dan de noemer kan zijn.
Bijvoorbeeld: 5/4 betekent dat we meer dan één 'gehele' hebben, want we hebben 5 delen van iets dat in 4 delen verdeeld is.

Denk aan een taart die in 6 stukken is verdeeld. Als je 2 stukken neemt, dan is de teller 2, omdat je 2 stukken hebt. Als je alle 6 stukken neemt, dan is de teller 6, en heb je 6/6 van de taart, oftewel de hele taart.

De Noemer: Het Totale Aantal Delen

De noemer is het getal dat onder de breukstreep staat. Het vertelt ons in hoeveel gelijke delen het geheel is verdeeld. In het pizza-voorbeeld is de noemer 8. Dit betekent dat de pizza in 8 gelijke stukken is gesneden.

De noemer geeft aan hoe groot elk deel is.
De noemer kan nooit nul zijn! Delen door nul is wiskundig ongedefinieerd.
Bijvoorbeeld: als de noemer 4 is, dan is elk deel 1/4 van het geheel.

Stel je voor dat je een reep chocola hebt die in 10 stukjes is verdeeld. De noemer is dan 10, omdat de reep in 10 stukjes is verdeeld. Of je er nu 1 stukje, 5 stukjes of alle 10 stukjes opeet, de noemer blijft altijd 10, zolang de reep in 10 stukjes verdeeld is.

Teller en Noemer in Actie: Voorbeelden

Laten we een paar voorbeelden bekijken om het concept van teller en noemer nog duidelijker te maken:

1/2: De noemer (2) vertelt ons dat iets in twee gelijke delen is verdeeld. De teller (1) vertelt ons dat we één van die delen hebben. Denk aan de helft van een appel.
3/4: De noemer (4) vertelt ons dat iets in vier gelijke delen is verdeeld. De teller (3) vertelt ons dat we drie van die delen hebben. Denk aan driekwart van een glas water.
7/10: De noemer (10) vertelt ons dat iets in tien gelijke delen is verdeeld. De teller (7) vertelt ons dat we zeven van die delen hebben. Denk aan zeven van de tien snoepjes in een zak.

Voorbeeld 1: Een verjaardagstaart

Op een verjaardag is er een taart die in 12 stukken is gesneden. De noemer is dus 12. Als er 5 kinderen een stuk taart eten, dan is de teller 5. De breuk die het deel van de taart representeert dat opgegeten is, is 5/12.

Voorbeeld 2: Een pizza avond

Je bestelt een pizza die in 8 stukken is gesneden. Je eet zelf 3 stukken en je vriend eet er 2. De totale hoeveelheid pizza die gegeten is, kan als volgt berekend worden:

Jij: 3/8

Vriend: 2/8

Samen: 3/8 + 2/8 = 5/8. De teller is 5 (het totale aantal gegeten stukken) en de noemer is 8 (het totale aantal stukken waarin de pizza was verdeeld).

Waarom Zijn Tellers en Noemers Belangrijk?

Begrip van tellers en noemers is cruciaal voor veel wiskundige concepten, zoals:

Breuken vereenvoudigen: Je kunt een breuk vereenvoudigen door de teller en de noemer door hetzelfde getal te delen. Bijvoorbeeld, 4/8 kan vereenvoudigd worden tot 1/2.
Breuken vergelijken: Om breuken te vergelijken, moeten ze dezelfde noemer hebben. Je kunt breuken gelijknamig maken door de teller en noemer van beide breuken met een geschikt getal te vermenigvuldigen.
Breuken optellen en aftrekken: Breuken kunnen alleen worden opgeteld of afgetrokken als ze dezelfde noemer hebben.
Rekenen met verhoudingen en percentages: Breuken vormen de basis van verhoudingen en percentages.
Probleemoplossing in het dagelijks leven: Van het koken met recepten tot het berekenen van kortingen in de winkel, breuken zijn overal!

Veelgemaakte Fouten en Hoe Ze Te Vermijden

Sommige veelgemaakte fouten met betrekking tot tellers en noemers zijn:

De teller en noemer verwisselen: Zorg ervoor dat je onthoudt dat de teller boven de breukstreep staat en de noemer eronder.
Breuken optellen of aftrekken zonder dezelfde noemer: Dit is een veelgemaakte fout. Zorg er altijd voor dat de breuken dezelfde noemer hebben voordat je ze optelt of aftrekt.
De noemer negeren bij het vereenvoudigen: Je moet zowel de teller als de noemer door hetzelfde getal delen om een breuk te vereenvoudigen.
Denken dat een grotere noemer altijd een grotere breuk betekent: Dit is niet altijd waar. Bijvoorbeeld, 1/2 is groter dan 1/4. Het is belangrijk om de teller ook in overweging te nemen.

Tips voor het Beter Begrijpen van Breuken

Hier zijn een paar tips om je te helpen breuken beter te begrijpen:

Gebruik visuele hulpmiddelen: Teken cirkels, vierkanten of rechthoeken en verdeel ze in gelijke delen om breuken te visualiseren.
Gebruik concrete voorbeelden: Denk aan pizza's, taarten, chocoladerepen of andere alledaagse objecten die je gemakkelijk in stukken kunt verdelen.
Oefen, oefen, oefen: Hoe meer je met breuken oefent, hoe beter je ze zult begrijpen. Er zijn veel online bronnen en werkboeken beschikbaar om je te helpen oefenen.
Vraag om hulp: Als je moeite hebt met breuken, aarzel dan niet om je leraar, een vriend of familielid om hulp te vragen.

Breuken in het Dagelijks Leven

Breuken zijn overal om ons heen, ook al realiseren we ons dat misschien niet altijd. Hier zijn enkele voorbeelden:

Koken en bakken: Recepten gebruiken vaak breuken om de hoeveelheid ingrediënten aan te geven. Bijvoorbeeld, 1/2 theelepel zout of 3/4 kopje bloem.
Tijd: Een half uur is 1/2 van een uur. Een kwartier is 1/4 van een uur.
Meten: Als je iets meet, gebruik je vaak breuken. Bijvoorbeeld, 2 1/2 centimeter.
Geld: 50 cent is 1/2 van een euro. 25 cent is 1/4 van een euro.
Sport: In sporten zoals basketbal en honkbal worden vaak breuken gebruikt om statistieken weer te geven.

Door deze alledaagse voorbeelden te herkennen, kun je het belang van breuken beter waarderen en ze gemakkelijker begrijpen.

Conclusie

De teller en de noemer zijn de bouwstenen van breuken. Door te begrijpen wat ze betekenen en hoe ze werken, open je een hele nieuwe wereld van wiskundige mogelijkheden. We hopen dat dit artikel je heeft geholpen om de basisprincipes van breuken beter te begrijpen. Blijf oefenen en experimenteren, en voor je het weet, ben je een breuken-expert! Onthoud: de noemer noemt hoe groot elk deel is, en de teller telt hoeveel delen je hebt. Nu je de basisprincipes kent, kun je vol vertrouwen verder bouwen aan je wiskundige kennis. Veel succes!