Wat Is De Stelling Van Pythagoras

Heb je je ooit afgevraagd hoe aannemers bepalen of een muur echt recht is, of hoe piloten de kortste route tussen twee steden berekenen? Achter veel van deze alledaagse toepassingen zit een fundamenteel wiskundig principe: de stelling van Pythagoras. Misschien heb je de naam wel eens gehoord in de wiskundeles, maar de relevantie ervan is vaak verborgen achter complexe formules. Laten we eens dieper duiken en de stelling van Pythagoras ontrafelen, en ontdekken hoe deze simpele, maar krachtige formule de wereld om ons heen vormgeeft.

Wat is de Stelling van Pythagoras?

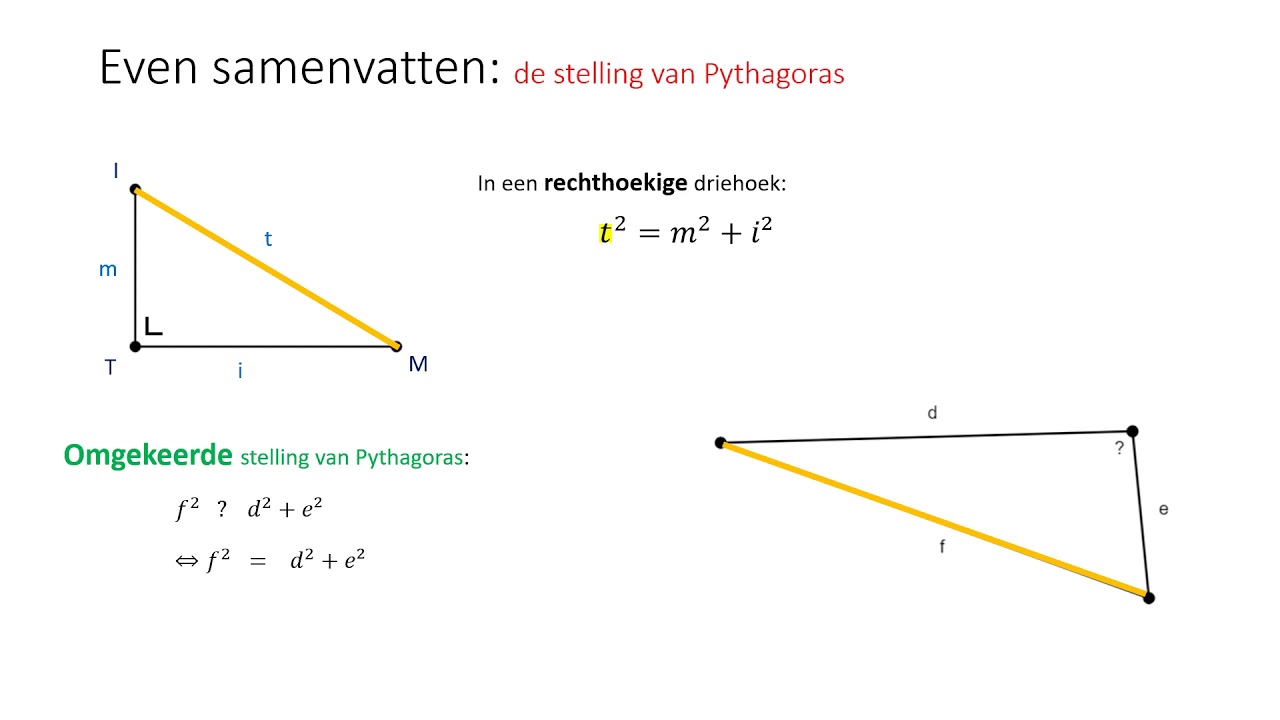
De stelling van Pythagoras is een fundamenteel principe in de meetkunde dat de relatie beschrijft tussen de zijden van een rechthoekige driehoek. Een rechthoekige driehoek is een driehoek met één hoek van precies 90 graden, ook wel een rechte hoek genoemd.

De stelling stelt dat:

In een rechthoekige driehoek is het kwadraat van de lengte van de schuine zijde (de zijde tegenover de rechte hoek) gelijk aan de som van de kwadraten van de lengtes van de andere twee zijden (de rechthoekszijden).

Dit kan worden uitgedrukt met de volgende formule:

a² + b² = c²

Waar:

a en b de lengtes zijn van de rechthoekszijden.
c de lengte is van de schuine zijde (hypotenusa).

Laten we dit visualiseren met een simpel voorbeeld. Stel je een rechthoekige driehoek voor waarbij de ene rechthoekszijde 3 cm lang is (a = 3) en de andere rechthoekszijde 4 cm lang is (b = 4). Om de lengte van de schuine zijde (c) te vinden, kunnen we de stelling van Pythagoras gebruiken:

3² + 4² = c²

9 + 16 = c²

25 = c²

c = √25

c = 5

Dus, de lengte van de schuine zijde is 5 cm.

Waarom is de Stelling van Pythagoras Belangrijk?

De stelling van Pythagoras is veel meer dan alleen een wiskundige formule. Het is een fundamenteel hulpmiddel dat in een breed scala aan disciplines wordt gebruikt. Hier zijn enkele voorbeelden van de praktische toepassingen:

Bouwkunde en Constructie

Aannemers gebruiken de stelling om er zeker van te zijn dat gebouwen rechte hoeken hebben en dat muren en funderingen stabiel zijn. Ze kunnen de stelling gebruiken om de lengte van een dakspant te berekenen, de hoogte van een gevel te bepalen, of te verifiëren of een fundering perfect rechthoekig is. Zonder de stelling van Pythagoras zouden gebouwen aanzienlijk minder stabiel en betrouwbaar zijn.

Navigatie

Piloten en zeelieden gebruiken de stelling om de kortste afstand tussen twee punten te berekenen. Hoewel de aarde rond is, kan op kleine schaal een plat vlak benaderd worden, waardoor de stelling van Pythagoras toepasbaar is. GPS-systemen maken ook gebruik van de stelling om locaties te bepalen, alhoewel in complexere berekeningen met geografische coördinaten.

Landmeetkunde

Landmeters gebruiken de stelling om landgrenzen te bepalen, hoogtes te meten en kaarten te maken. De stelling helpt bij het uitzetten van percelen en het bepalen van de afmetingen van land.

Grafisch Ontwerp en Computer Graphics

In de computer graphics wordt de stelling gebruikt om afstanden tussen punten te berekenen, perspectieven te creëren en bewegingen te simuleren. Denk bijvoorbeeld aan het berekenen van botsingen tussen objecten in een videospel of het creëren van realistische schaduwen.

Wiskunde en Natuurkunde

De stelling van Pythagoras is een hoeksteen van de meetkunde en wordt gebruikt in vele andere wiskundige en natuurkundige concepten, zoals trigonometrie, vectoralgebra en relativiteitstheorie.

Mogelijke Tegenwerpingen en Misvattingen

Hoewel de stelling van Pythagoras een fundamenteel principe is, zijn er enkele veel voorkomende misvattingen en tegenwerpingen die we moeten aanpakken:

De stelling geldt alleen voor rechthoekige driehoeken: Dit is een cruciale beperking. De stelling van Pythagoras kan niet worden gebruikt voor driehoeken die geen rechte hoek hebben. Voor niet-rechthoekige driehoeken zijn er andere trigonometrische regels, zoals de sinus- en cosinusregel.
De stelling is te abstract en niet relevant voor het dagelijks leven: Zoals we hebben gezien, heeft de stelling van Pythagoras veel praktische toepassingen in de bouwkunde, navigatie, landmeetkunde en nog veel meer. Hoewel de formule zelf misschien abstract lijkt, zijn de gevolgen ervan zeer tastbaar.
De stelling is moeilijk te begrijpen: Met de juiste visualisaties en voorbeelden kan de stelling van Pythagoras op een begrijpelijke manier worden uitgelegd. Het is belangrijk om de basisprincipes van meetkunde en algebra te begrijpen, maar met geduld en oefening kan iedereen de stelling van Pythagoras leren beheersen.

Een Oplossingsgerichte Aanpak

Hoe kunnen we de stelling van Pythagoras beter begrijpen en toepassen?

Visuele hulpmiddelen gebruiken: Diagrammen en animaties kunnen helpen om de relatie tussen de zijden van een rechthoekige driehoek te visualiseren.
Praktische voorbeelden oefenen: Werk door verschillende voorbeelden en problemen om de toepassing van de stelling te oefenen.
Online resources raadplegen: Er zijn veel online tutorials, video's en oefeningen beschikbaar om de stelling van Pythagoras te leren.
Interactieve tools gebruiken: Er zijn interactieve tools waarmee je de zijden van een rechthoekige driehoek kunt aanpassen en de resultaten direct kunt zien.

Voorbeeld: Een Ladder tegen een Muur

Stel je voor dat je een ladder tegen een muur zet. De ladder is 5 meter lang en de voet van de ladder staat 3 meter van de muur af. Hoe hoog reikt de ladder op de muur?

In dit geval vormt de muur, de grond en de ladder een rechthoekige driehoek. De ladder is de schuine zijde (c = 5), de afstand van de muur tot de voet van de ladder is een rechthoekszijde (a = 3), en de hoogte van de ladder op de muur is de andere rechthoekszijde (b = ?).

We kunnen de stelling van Pythagoras gebruiken om b te vinden:

a² + b² = c²

3² + b² = 5²

9 + b² = 25

b² = 25 - 9

b² = 16

b = √16

b = 4

Dus, de ladder reikt 4 meter hoog op de muur.

De Toekomst van de Stelling van Pythagoras

Hoewel de stelling van Pythagoras al duizenden jaren oud is, blijft het een relevante en onmisbare tool in de moderne wereld. Met de voortdurende ontwikkeling van technologie en wetenschap zullen er ongetwijfeld nieuwe en innovatieve toepassingen van de stelling van Pythagoras ontstaan. Het is een tijdloos principe dat de basis vormt voor veel van onze technologische en wetenschappelijke vooruitgang.

De stelling van Pythagoras is niet alleen een formule, maar een manier om de wereld om ons heen te begrijpen en te meten. Het leert ons dat eenvoudige principes vaak de sleutel zijn tot het oplossen van complexe problemen. En wie weet, misschien inspireert de stelling van Pythagoras je wel om zelf nieuwe wiskundige ontdekkingen te doen!

Na het lezen over de vele toepassingen van de stelling van Pythagoras, hoe zou jij deze kennis kunnen gebruiken in je eigen vakgebied of dagelijks leven? Of misschien ga je nu met een andere blik naar de gebouwen om je heen kijken?