Wat Is Een Gelijkbenige Driehoek

In de wereld van de meetkunde, en specifiek binnen de studie van veelhoeken, neemt de gelijkbenige driehoek een belangrijke plaats in. Deze driehoeksvorm, met zijn specifieke eigenschappen en toepassingen, is niet alleen een fundamenteel concept in de wiskunde, maar duikt ook verrassend vaak op in onze alledaagse omgeving. Laten we dieper ingaan op wat een gelijkbenige driehoek precies is, welke kenmerken deze definieren, en hoe deze verschilt van andere soorten driehoeken.

Definitie van een Gelijkbenige Driehoek

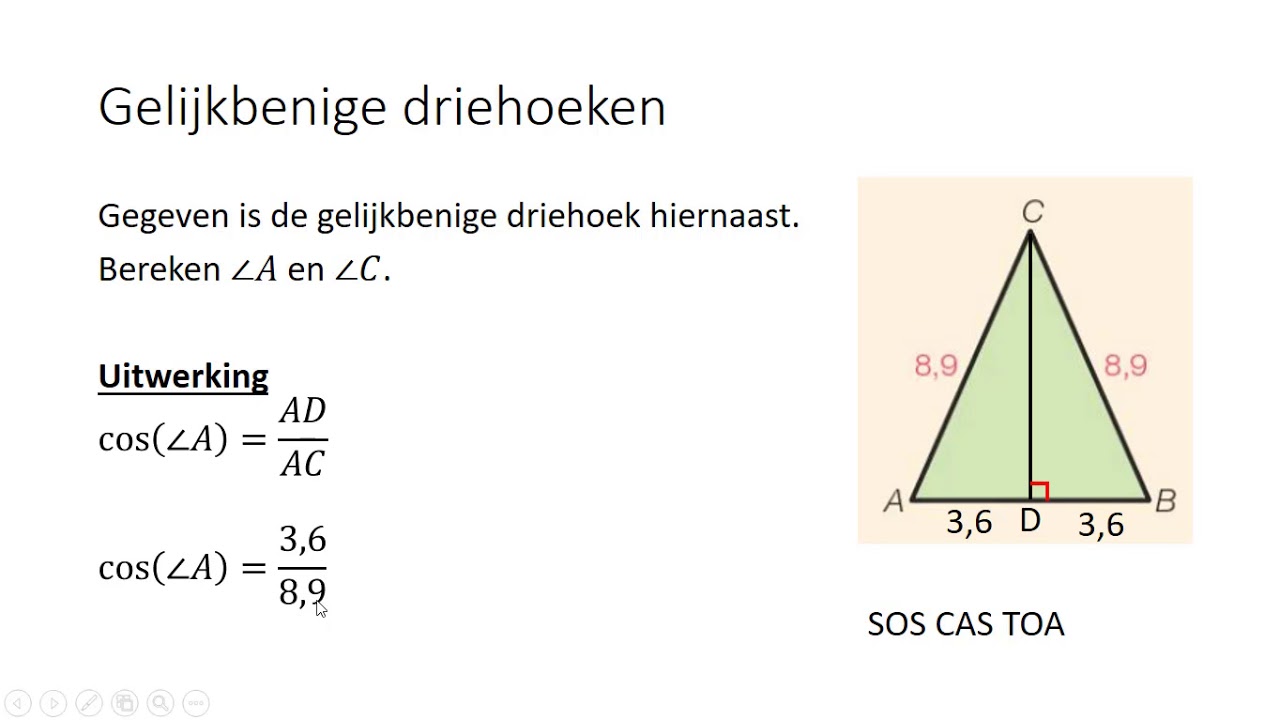
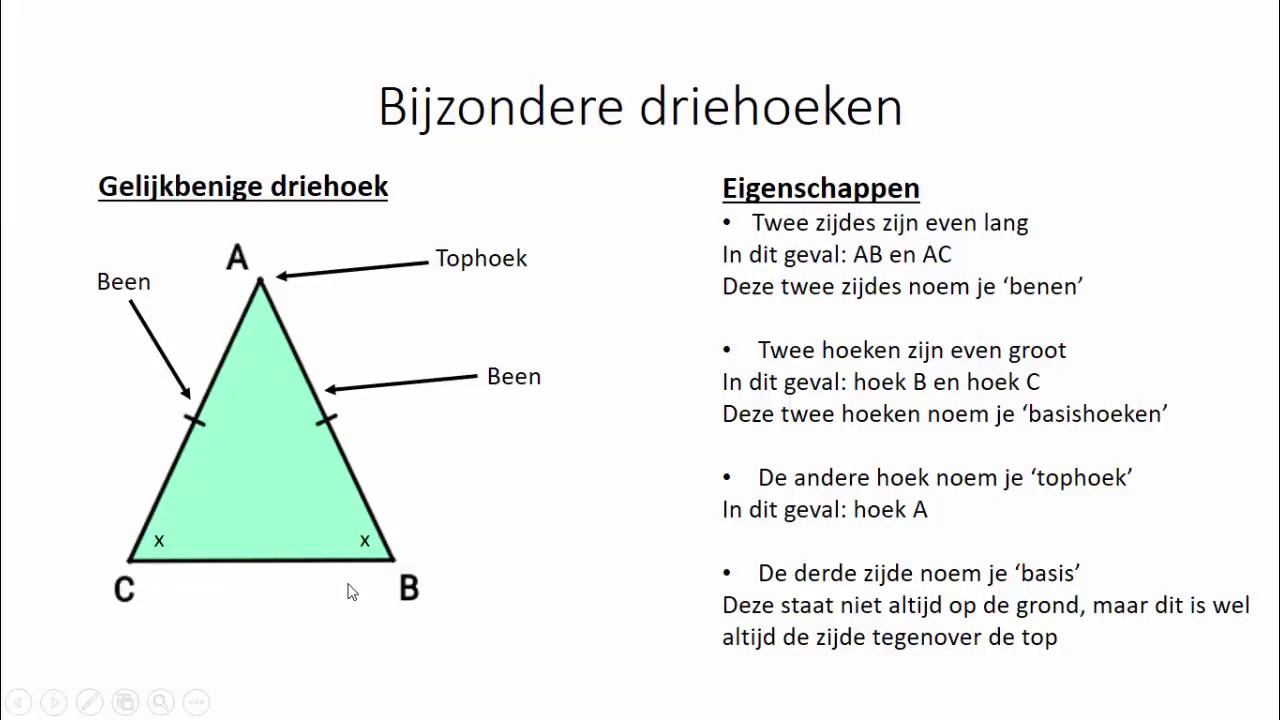
Een gelijkbenige driehoek is gedefinieerd als een driehoek met minstens twee zijden van gelijke lengte. Deze gelijke zijden worden de benen van de driehoek genoemd. De derde zijde, die mogelijk een andere lengte heeft, wordt de basis genoemd. De hoek tussen de twee benen wordt de tophoek genoemd, terwijl de twee hoeken aan de basis de basishoeken worden genoemd.

Kenmerkende Eigenschappen

Naast de definitie van twee gelijke zijden, zijn er een aantal andere belangrijke eigenschappen die kenmerkend zijn voor een gelijkbenige driehoek:

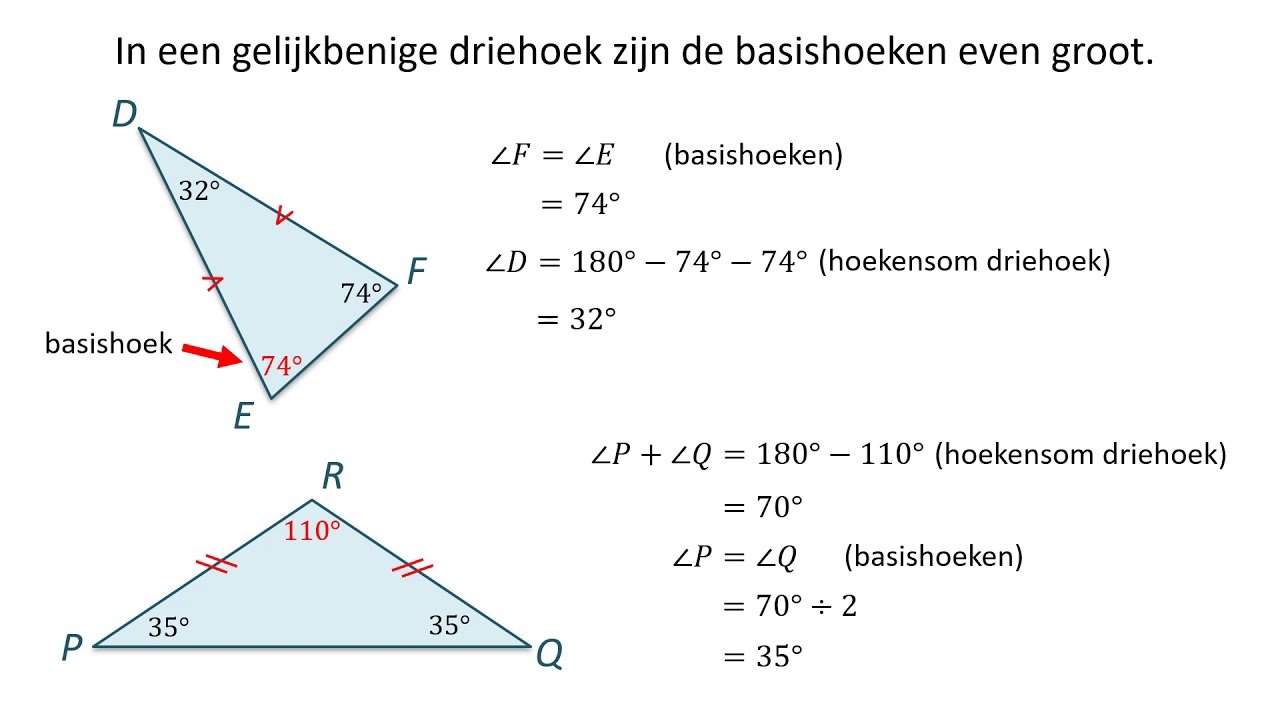
Gelijke Basishoeken: Een van de meest fundamentele eigenschappen is dat de basishoeken (de hoeken tegenover de gelijke zijden) altijd gelijk zijn. Dit is een direct gevolg van de gelijkbenige aard van de driehoek.
Symmetrie: Een gelijkbenige driehoek bezit lijnsymmetrie. Er is een denkbeeldige lijn, de symmetrieas, die van de top hoekloodrecht op de basis loopt. Deze lijn deelt de driehoek in twee identieke helften. Deze symmetrie maakt de gelijkbenige driehoek visueel aantrekkelijk en gemakkelijk te herkennen.
Hoogtelijn, Zwaartelijn en Bissectrice: De hoogtelijn (de lijn loodrecht op de basis vanuit de top), de zwaartelijn (de lijn van de top naar het midden van de basis) en de bissectrice (de lijn die de tophoek in twee gelijke hoeken verdeelt) vallen samen langs de symmetrieas. Dit is een unieke eigenschap die alleen geldt voor gelijkbenige (en gelijkzijdige) driehoeken.

Verschil met andere Driehoeken

Het is cruciaal om de gelijkbenige driehoek te onderscheiden van andere soorten driehoeken, zoals de gelijkzijdige driehoek en de ongelijkzijdige driehoek.

Gelijkbenige vs. Gelijkzijdige Driehoek

Een gelijkzijdige driehoek is een speciaal geval van een gelijkbenige driehoek. Terwijl een gelijkbenige driehoek *minstens* twee gelijke zijden heeft, heeft een gelijkzijdige driehoek drie gelijke zijden. Dit betekent dat alle drie de hoeken in een gelijkzijdige driehoek ook gelijk zijn (elk 60 graden). Daarom is elke gelijkzijdige driehoek ook een gelijkbenige driehoek, maar niet elke gelijkbenige driehoek is een gelijkzijdige driehoek.

Gelijkbenige vs. Ongelijkzijdige Driehoek

Een ongelijkzijdige driehoek daarentegen, heeft drie zijden van verschillende lengtes. Bijgevolg zijn ook alle drie de hoeken verschillend. Een ongelijkzijdige driehoek bezit geen lijnsymmetrie, in tegenstelling tot de gelijkbenige driehoek. De relaties tussen de zijden en hoeken zijn complexer in een ongelijkzijdige driehoek dan in een gelijkbenige of gelijkzijdige driehoek.

Berekeningen in een Gelijkbenige Driehoek

Verschillende berekeningen kunnen worden uitgevoerd op een gelijkbenige driehoek, waaronder het berekenen van de oppervlakte, de omtrek en de lengte van de hoogtelijn.

Oppervlakte

De oppervlakte van een gelijkbenige driehoek kan worden berekend met behulp van verschillende formules, afhankelijk van de beschikbare informatie:

Basis en Hoogte: Als de lengte van de basis (b) en de hoogte (h) bekend zijn, kan de oppervlakte (A) worden berekend met de formule: A = (1/2) * b * h.
Twee Zijden en de Ingesloten Hoek: Als de lengte van twee zijden (a en b) en de ingesloten hoek (γ) bekend zijn, kan de oppervlakte worden berekend met de formule: A = (1/2) * a * b * sin(γ). In het geval van een gelijkbenige driehoek, waarbij a = b, wordt dit: A = (1/2) * a² * sin(γ), waarbij γ de tophoek is.
Formule van Heron: Als de lengte van alle drie de zijden bekend is, kan de formule van Heron worden gebruikt. Eerst bereken je de halve omtrek (s): s = (a + b + c) / 2. Vervolgens bereken je de oppervlakte: A = √(s(s-a)(s-b)(s-c)).

Omtrek

De omtrek van een gelijkbenige driehoek is eenvoudig te berekenen door de lengtes van alle drie de zijden op te tellen. Als de lengte van de twee gelijke zijden (a) en de lengte van de basis (b) bekend zijn, is de omtrek (P) gelijk aan: P = 2a + b.

Hoogte

De hoogte van een gelijkbenige driehoek kan worden berekend met behulp van de stelling van Pythagoras. Als de lengte van een van de gelijke zijden (a) en de lengte van de halve basis (b/2) bekend zijn, kan de hoogte (h) worden berekend met de formule: h = √(a² - (b/2)²). Dit is omdat de hoogtelijn de gelijkbenige driehoek verdeelt in twee rechthoekige driehoeken.

Real-World Voorbeelden en Data

Gelijkbenige driehoeken komen verrassend vaak voor in de echte wereld. Hun stabiele en esthetisch aangename vorm maakt ze populair in verschillende toepassingen:

Architectuur: Veel daken van huizen en gebouwen hebben de vorm van een gelijkbenige driehoek. Dit zorgt voor een goede afvoer van regenwater en sneeuw. Ook in bruggen en andere constructies worden vaak gelijkbenige driehoeken gebruikt voor hun structurele stabiliteit.
Design: De vorm van een gelijkbenige driehoek wordt vaak gebruikt in logo's, symbolen en andere grafische ontwerpen. De eenvoud en symmetrie van de vorm maken hem gemakkelijk herkenbaar en visueel aantrekkelijk. Denk bijvoorbeeld aan het logo van de Toblerone chocoladereep.
Natuur: In de natuur komen gelijkbenige driehoeken minder vaak voor in perfecte vorm, maar benaderingen ervan zijn wel te vinden. Bijvoorbeeld, de vorm van sommige bladeren of de hoek van een tak aan een boomstam kunnen een gelijkbenige driehoek benaderen.
Techniek: Verschillende soorten gereedschap, zoals bepaalde soorten schroevendraaiers of messen, kunnen de vorm van een gelijkbenige driehoek hebben. Ook in meetinstrumenten, zoals de gradenboog, wordt gebruik gemaakt van gelijkbenige driehoeken om hoeken nauwkeurig te meten.

Er is geen specifieke data die de frequentie van gelijkbenige driehoeken in de natuur meet. Echter, wiskundige modellen die de optimale hoeken voor bijvoorbeeld boomvertakkingen berekenen, laten zien dat de hoeken vaak dicht bij die van een gelijkbenige driehoek liggen, wat een indicatie is van de efficiëntie van deze vorm.

Conclusie

De gelijkbenige driehoek is een fundamenteel en veelzijdig geometrisch figuur met duidelijke eigenschappen en talloze toepassingen. Van de architectuur tot de natuur, deze driehoeksvorm is alomtegenwoordig. Het begrijpen van de definitie, eigenschappen en berekeningen van een gelijkbenige driehoek is essentieel voor studenten van wiskunde en meetkunde, maar ook voor iedereen die geïnteresseerd is in de wereld om hen heen.

Neem de tijd om de wereld om je heen te observeren en je zult verrast zijn over hoe vaak je gelijkbenige driehoeken tegenkomt. Probeer de eigenschappen die je hebt geleerd toe te passen en bereken bijvoorbeeld de oppervlakte van een dak in de vorm van een gelijkbenige driehoek. Door je kennis te gebruiken, zul je de schoonheid en functionaliteit van de gelijkbenige driehoek nog meer waarderen.