Wat Is Een Omgekeerd Evenredig Verband
In de wiskunde en natuurwetenschappen komen we regelmatig relaties tegen tussen verschillende grootheden. Een van deze relaties is de omgekeerd evenredige, ook wel indirect evenredige, relatie. Dit artikel duikt dieper in wat een omgekeerd evenredig verband precies inhoudt, hoe je het herkent, en waar je het in de praktijk tegenkomt.
Wat is een Omgekeerd Evenredig Verband?
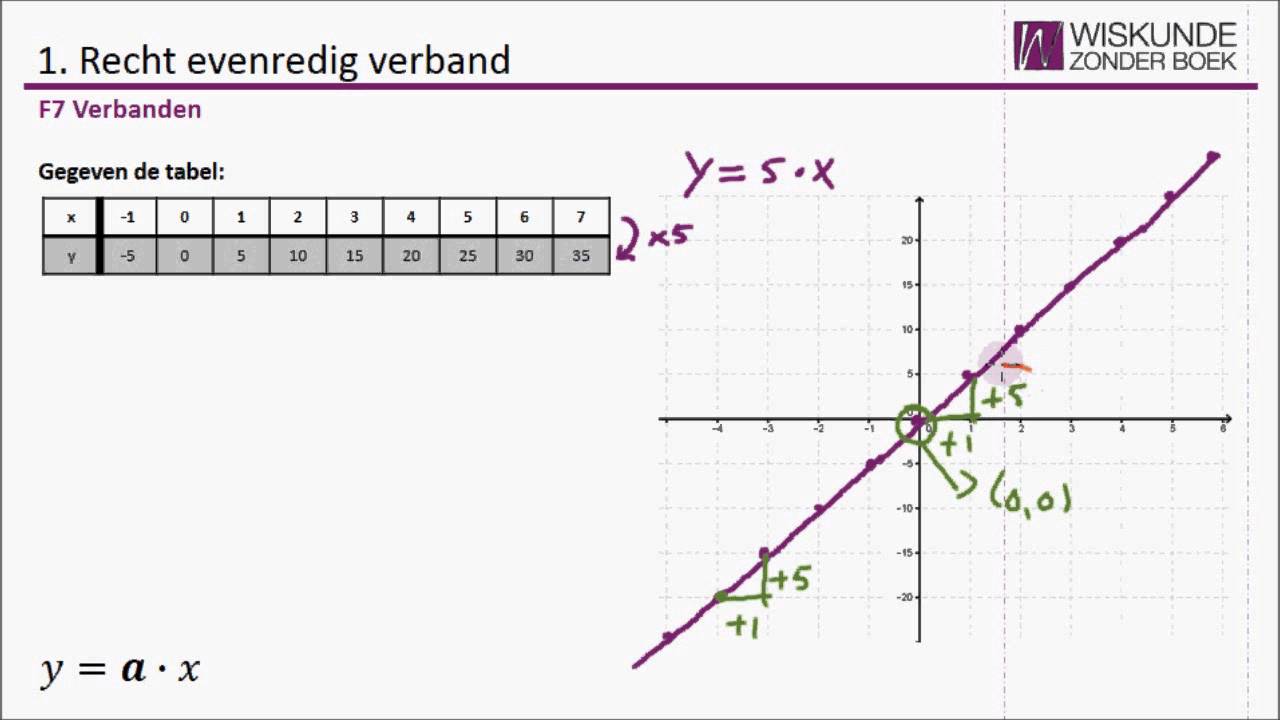
Een omgekeerd evenredig verband beschrijft een relatie tussen twee variabelen waarbij, als de ene variabele toeneemt, de andere variabele evenredig afneemt. Cruciaal is dat het product van de twee variabelen constant blijft. Dit staat in schril contrast met een recht evenredig verband, waarbij de variabelen in dezelfde richting veranderen (als de ene toeneemt, neemt de andere ook toe).
Wiskundig kunnen we dit als volgt uitdrukken:
y = k / x
Waar:
- y en x de variabelen zijn
- k de evenredigheidsconstante is. Deze constante bepaalt de exacte relatie tussen de variabelen.
Kenmerken van een Omgekeerd Evenredig Verband
Er zijn een paar belangrijke kenmerken waaraan je een omgekeerd evenredig verband kunt herkennen:
- Als x verdubbelt, halveert y (en vice versa). Dit is de kern van de omgekeerde relatie.
- Het product van x en y is altijd constant. Oftewel, x * y = k. Dit kan gebruikt worden om de evenredigheidsconstante te berekenen of om te controleren of er daadwerkelijk sprake is van een omgekeerd evenredig verband.
- De grafiek van een omgekeerd evenredig verband is een hyperbool. Dit is een vloeiende curve die asymptotisch nadert tot de x- en y-assen, maar ze nooit raakt.
Hoe Herken Je een Omgekeerd Evenredig Verband in Data?
Soms krijg je data gepresenteerd zonder expliciet te weten of er een omgekeerd evenredig verband is. Hier zijn een paar manieren om het te identificeren:
- Analyseer de verandering in waarden. Kijk of een verandering in de ene variabele resulteert in een omgekeerde proportionele verandering in de andere. Bijvoorbeeld, als je een tabel hebt met data, kijk dan of een verdubbeling van x resulteert in een halvering van y.
- Bereken het product van de variabelen. Vermenigvuldig de corresponderende waarden van x en y. Als het product ongeveer constant is (houd rekening met meetfouten of afrondingen), dan is er waarschijnlijk een omgekeerd evenredig verband.
- Maak een spreidingsdiagram. Visualiseer de data in een spreidingsdiagram. Als de punten een hyperbool-achtige vorm aannemen, dan is dat een sterke indicatie van een omgekeerd evenredig verband.
Voorbeelden van Omgekeerd Evenredige Verbanden in de Praktijk
Omgekeerd evenredige verbanden komen veel voor in verschillende disciplines:
Natuurkunde
Een klassiek voorbeeld is de relatie tussen de druk (P) en het volume (V) van een ideaal gas bij constante temperatuur (Wet van Boyle):
P * V = k
Dit betekent dat als je het volume van een gas verkleint (bijvoorbeeld door een zuiger in een cilinder te duwen), de druk toeneemt. De evenredigheidsconstante k is gerelateerd aan de hoeveelheid gas en de temperatuur.
Een ander voorbeeld is de relatie tussen de lichtsterkte (I) van een puntbron en de afstand (r) tot de bron:
I = k / r²
Dit betekent dat hoe verder je van een lamp afstaat, hoe zwakker het licht wordt. De lichtsterkte neemt af met het kwadraat van de afstand.
Economie
In de economie kan de prijs (P) van een product omgekeerd evenredig zijn met de gevraagde hoeveelheid (Q) (onder bepaalde voorwaarden):
P = k / Q
Dit betekent dat als de prijs van een product stijgt, de gevraagde hoeveelheid (meestal) afneemt, en vice versa. De evenredigheidsconstante k hangt af van factoren zoals de vraag naar het product en de beschikbaarheid van alternatieven.
Snelheid en Tijd
De relatie tussen snelheid (v) en tijd (t) voor een bepaalde afstand (d) is ook omgekeerd evenredig:
v = d / t of d = v * t
Als de afstand constant is, geldt: v * t = k (waarbij k = d). Dit betekent dat als je sneller reist, je minder tijd nodig hebt om dezelfde afstand af te leggen.
Voorbeeld met Data: Arbeiders en Tijd om een Klus te Klaren
Stel je voor dat je een klus hebt die geklaard moet worden. Het aantal arbeiders dat aan de klus werkt en de tijd die nodig is om de klus te klaren, zijn omgekeerd evenredig (onder de aanname dat alle arbeiders even efficiënt zijn). Laten we de volgende data bekijken:
| Aantal Arbeiders (x) | Tijd om de Klus te Klaren (uren) (y) |
|---|---|
| 1 | 24 |
| 2 | 12 |
| 3 | 8 |
| 4 | 6 |
Als je het product van het aantal arbeiders en de tijd berekent, zul je zien dat het constant is: 1 * 24 = 24, 2 * 12 = 24, 3 * 8 = 24, 4 * 6 = 24. De evenredigheidsconstante is dus 24. Dit betekent dat het 24 "arbeidersuren" kost om de klus te klaren.
We kunnen dit gebruiken om te voorspellen hoeveel tijd het zou kosten met een ander aantal arbeiders. Bijvoorbeeld, als je 6 arbeiders hebt, dan is de tijd 24 / 6 = 4 uur.
Wanneer is een Omgekeerd Evenredig Verband *Niet* van Toepassing?
Het is belangrijk te onthouden dat niet alle relaties tussen variabelen omgekeerd evenredig zijn. Er zijn situaties waarin een omgekeerd evenredig verband *niet* van toepassing is:
- Complexere relaties: Soms is de relatie tussen variabelen veel complexer en kan deze niet worden beschreven door een eenvoudige omgekeerd evenredige functie. Er kunnen andere variabelen in het spel zijn die de relatie beïnvloeden.
- Grenzen: In sommige gevallen zijn er grenzen aan de waarden van de variabelen. Bijvoorbeeld, in het voorbeeld van arbeiders en tijd, kun je niet oneindig veel arbeiders toevoegen en verwachten dat de tijd tot nul nadert. Er is een praktisch minimum aan de tijd die nodig is om de klus te klaren.
- Andere verbanden: Er kunnen ook andere soorten verbanden zijn, zoals een recht evenredig verband, een kwadratische relatie, of een exponentiële relatie.
Conclusie
Een omgekeerd evenredig verband is een krachtig concept dat helpt om relaties tussen variabelen te begrijpen waarbij de ene variabele afneemt als de andere toeneemt, en vice versa. Het herkennen van deze verbanden is essentieel in diverse vakgebieden, van natuurkunde tot economie. Door de kenmerken, de wiskundige formulering en de praktische voorbeelden te begrijpen, kun je deze relaties effectiever analyseren en toepassen.
Dus, de volgende keer dat je data analyseert of een probleem probeert op te lossen, overweeg dan of er mogelijk sprake is van een omgekeerd evenredig verband. Het kan je helpen om de onderliggende mechanismen te begrijpen en betere voorspellingen te doen. Blijf leren en ontdek de verborgen patronen in de wereld om je heen!
Bekijk ook deze gerelateerde berichten:
- Wat Is De Vertelde Tijd
- Welke Medicijnen Verhogen Gamma Gt
- Wanneer Legt De Koekoek Een Ei
- Wat Zet Je In Motivatiebrief
- Hoeveel Poten Heeft Een Kreeft
- Hoe Bereken Je De Soortelijke Warmte
- Ere Zij God In De Hoogste Hemelen
- Hoeveel Liter Is 100 Gram
- Berekening Bruto Naar Netto Ww Uitkering
- Geruite Wollen Stof Waarvan Schotse Kilt Gemaakt Worden
