Wat Is Een Vergelijking Wiskunde

In de wondere wereld van de wiskunde kom je vaak de term "vergelijking" tegen. Maar wat precies is een vergelijking, en waarom is het zo'n fundamenteel concept? Dit artikel duikt diep in de betekenis van een vergelijking, verkent de verschillende soorten, en laat zien hoe ze worden gebruikt om problemen op te lossen, zowel in de wiskunde zelf als in de echte wereld.

Wat is een Vergelijking?

In de eenvoudigste bewoordingen is een vergelijking een wiskundige uitspraak die beweert dat twee uitdrukkingen aan elkaar gelijk zijn. Deze bewering wordt aangegeven door het gebruik van het gelijkteken (=). Een vergelijking kan variabelen bevatten, dit zijn symbolen (meestal letters) die staan voor onbekende waarden. Het doel bij het oplossen van een vergelijking is om de waarde(n) van deze variabelen te vinden die de vergelijking waar maken.

Denk aan een balans. Een vergelijking is als een perfect uitgebalanceerde weegschaal. Wat aan de ene kant van het gelijkteken staat, moet precies hetzelfde "gewicht" hebben als wat aan de andere kant staat. Als je aan één kant iets toevoegt of weghaalt, moet je hetzelfde doen aan de andere kant om de balans te bewaren.

Bestanddelen van een Vergelijking

Een vergelijking bestaat doorgaans uit de volgende elementen:

Termen: Dit zijn de afzonderlijke onderdelen van een vergelijking, gescheiden door plus- (+) of min- (-) tekens. Een term kan een constante (een getal), een variabele, of een product van een constante en een variabele zijn.
Variabelen: Dit zijn symbolen (meestal letters zoals x, y, z) die onbekende waarden vertegenwoordigen.
Coëfficiënten: Dit zijn de getallen die voor de variabelen staan. In de term 3x is 3 de coëfficiënt.
Constanten: Dit zijn getallen die geen variabelen bevatten.
Gelijkteken (=): Dit symbool geeft aan dat de expressie links van het teken gelijk is aan de expressie rechts van het teken.

Bijvoorbeeld, in de vergelijking 3x + 5 = 14:

3x en 5 zijn termen aan de linkerkant.
14 is een term aan de rechterkant.
x is de variabele.
3 is de coëfficiënt van x.
5 en 14 zijn constanten.

Soorten Vergelijkingen

Vergelijkingen kunnen in verschillende categorieën worden ingedeeld, afhankelijk van hun vorm en de complexiteit van de betrokken bewerkingen.

Lineaire Vergelijkingen

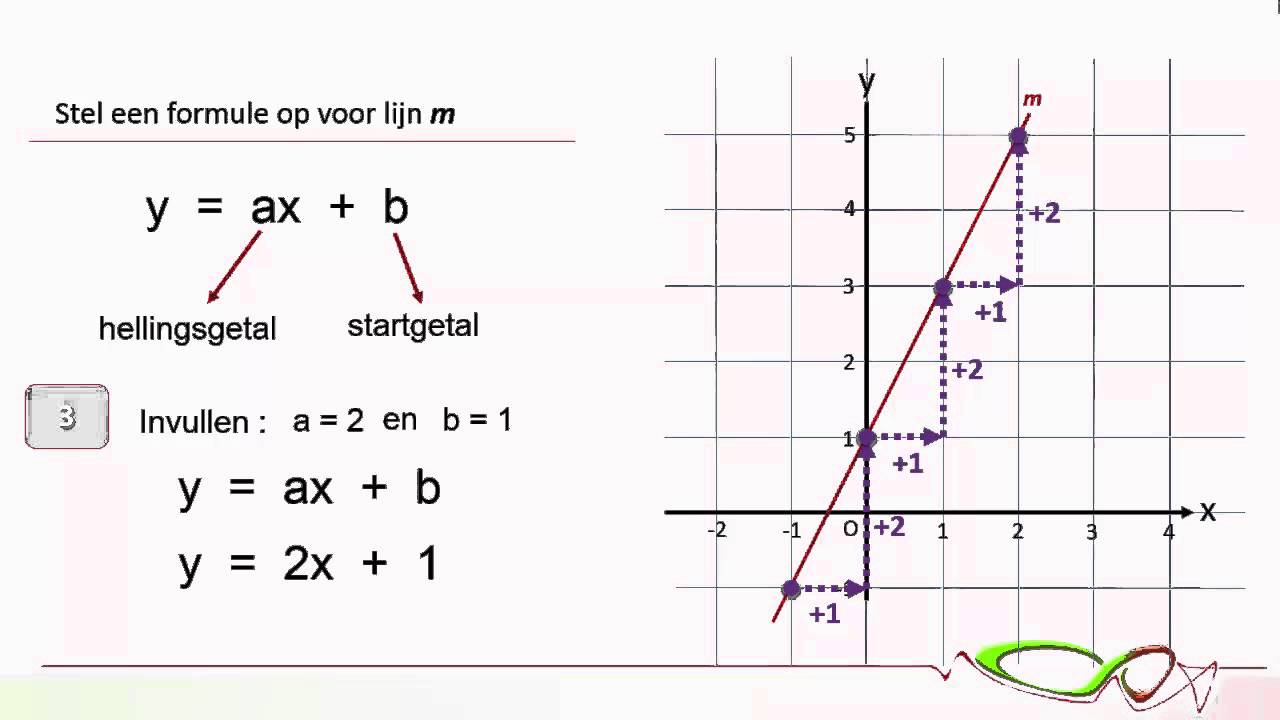
Een lineaire vergelijking is een vergelijking waarin de hoogste macht van de variabele 1 is. Deze vergelijkingen kunnen worden geschreven in de vorm ax + b = 0, waarbij a en b constanten zijn en x de variabele is. De grafiek van een lineaire vergelijking is een rechte lijn.

Voorbeelden:

2x + 3 = 7
y = 5x - 2

Kwadratische Vergelijkingen

Een kwadratische vergelijking is een vergelijking waarin de hoogste macht van de variabele 2 is. Deze vergelijkingen kunnen worden geschreven in de vorm ax² + bx + c = 0, waarbij a, b en c constanten zijn en x de variabele is. Kwadratische vergelijkingen kunnen nul, één of twee reële oplossingen hebben.

Voorbeelden:

x² - 4x + 3 = 0
2x² + 5x - 12 = 0

Stelsels van Vergelijkingen

Een stelsel van vergelijkingen bestaat uit twee of meer vergelijkingen met twee of meer variabelen. Het doel is om waarden voor de variabelen te vinden die alle vergelijkingen in het stelsel tegelijkertijd waar maken. Er zijn verschillende methoden om stelsels van vergelijkingen op te lossen, zoals substitutie, eliminatie en matrixmethoden.

Voorbeeld:

Het stelsel:

x + y = 5
x - y = 1

Heeft de oplossing x=3 en y=2.

Differentiaalvergelijkingen

Differentiaalvergelijkingen leggen een verband tussen een functie en haar afgeleiden. Ze worden veel gebruikt om processen te modelleren die in de tijd of ruimte veranderen, zoals de groei van een populatie, de beweging van een object of de verspreiding van warmte. Het oplossen van differentiaalvergelijkingen kan complex zijn en vereist vaak speciale technieken.

Voorbeeld:

dy/dx = ky (beschrijft exponentiële groei)

Andere Soorten

Er bestaan nog vele andere soorten vergelijkingen, zoals:

Polynomiale vergelijkingen: Vergelijkingen met een polynoom aan één kant van het gelijkteken.
Rationale vergelijkingen: Vergelijkingen met een rationale expressie (een breuk met polynomen) aan één kant van het gelijkteken.
Exponentiële vergelijkingen: Vergelijkingen waarin de variabele in de exponent staat.
Logaritmische vergelijkingen: Vergelijkingen waarin de variabele in een logaritme staat.
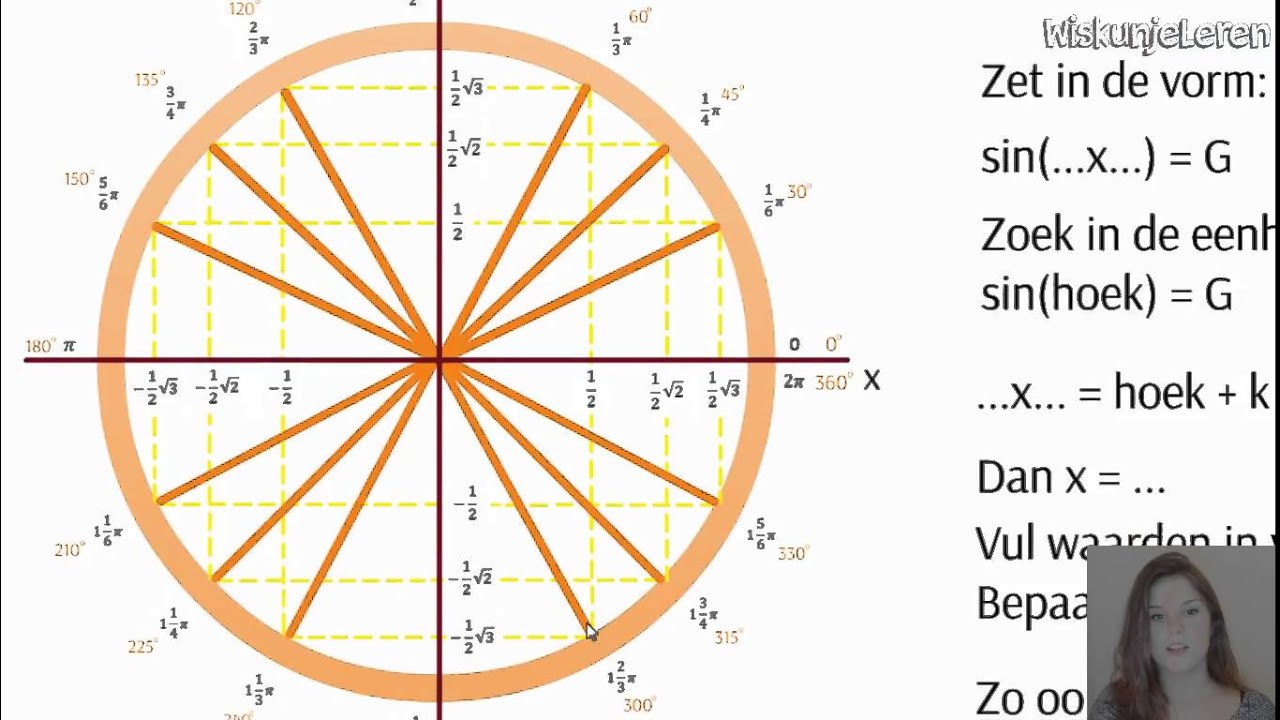
Trigonometrische vergelijkingen: Vergelijkingen met trigonometrische functies (sinus, cosinus, tangens, enz.).

Vergelijkingen in de Praktijk

Vergelijkingen zijn overal om ons heen. Ze zijn niet alleen een abstract concept in de wiskunde, maar een krachtig hulpmiddel voor het modelleren en begrijpen van de wereld om ons heen.

Natuurkunde

De natuurkunde is doordrenkt met vergelijkingen. De wetten van Newton, de vergelijkingen van Maxwell (elektromagnetisme), en Einsteins beroemde E=mc² zijn allemaal voorbeelden van vergelijkingen die de basis vormen van ons begrip van het universum.

Economie

Economische modellen maken veel gebruik van vergelijkingen om complexe systemen te beschrijven, zoals de relatie tussen vraag en aanbod, de inflatie, en de economische groei. Vergelijkingen worden gebruikt om voorspellingen te doen en beleidsbeslissingen te informeren.

Informatica

In de informatica worden vergelijkingen gebruikt om algoritmen te ontwerpen en te analyseren, datastructuren te modelleren, en computersystemen te simuleren. Bijvoorbeeld, de complexiteit van een algoritme kan worden uitgedrukt met behulp van vergelijkingen.

Engineering

Ingenieurs gebruiken vergelijkingen om bruggen te ontwerpen, vliegtuigen te bouwen, en elektronische circuits te ontwerpen. Vergelijkingen worden gebruikt om krachten, spanningen, stromen en andere relevante variabelen te berekenen.

Dagelijks Leven

Zelfs in het dagelijks leven gebruiken we impliciet vergelijkingen. Als je berekent hoeveel benzine je nodig hebt voor een reis, of hoeveel ingrediënten je nodig hebt voor een recept, ben je eigenlijk een vergelijking aan het oplossen. Budgettering is een andere vorm van het balanceren van een vergelijking: inkomsten moeten gelijk zijn aan uitgaven.

Data Analyse

In data analyse, lineaire regressie, een fundamentele techniek, maakt gebruik van lineaire vergelijkingen om de relatie tussen variabelen te modelleren. Stel je voor dat je de relatie tussen de advertentie-uitgaven en de verkoop wilt begrijpen. Een lineaire regressievergelijking kan worden gebruikt om te kwantificeren hoe een verandering in advertentie-uitgaven de verkoop beïnvloedt.

Voorbeeld: Een bedrijf analyseert de data en komt tot de volgende vergelijking: Verkoop = 10 + 5 * Advertentie_Uitgaven. Dit betekent dat voor elke euro die aan advertenties wordt uitgegeven, de verkoop met 5 euro toeneemt, met een basisverkoop van 10 euro, zelfs zonder advertenties.

Het Oplossen van Vergelijkingen

Het oplossen van een vergelijking betekent het vinden van de waarde(n) van de variabelen die de vergelijking waar maken. Er zijn verschillende technieken om vergelijkingen op te lossen, afhankelijk van het type vergelijking.

Enkele veelgebruikte technieken zijn:

Algebraïsche manipulatie: Het toepassen van algebraïsche bewerkingen (zoals optellen, aftrekken, vermenigvuldigen, delen) aan beide kanten van de vergelijking om de variabele te isoleren.
Substitutie: Het vervangen van een variabele door een uitdrukking die gelijk is aan die variabele.
Eliminatie: Het optellen of aftrekken van vergelijkingen om een variabele te elimineren.
Factoring: Het ontbinden van een polynoom in factoren.
Kwadratische formule: Een formule die gebruikt wordt om de oplossingen van een kwadratische vergelijking te vinden.
Numerieke methoden: Het gebruik van computerprogramma's om een benadering van de oplossing te vinden.

Conclusie

Een vergelijking is een fundamenteel concept in de wiskunde dat een bewering van gelijkheid tussen twee uitdrukkingen uitdrukt. Vergelijkingen komen in verschillende vormen en worden gebruikt om een breed scala aan problemen op te lossen, van eenvoudige algebraïsche problemen tot complexe wetenschappelijke en technische problemen. Het beheersen van de vaardigheid om vergelijkingen te begrijpen en op te lossen is essentieel voor succes in de wiskunde en vele andere disciplines.

Dus, duik erin, oefen en ontdek de kracht van vergelijkingen! Daag jezelf uit met verschillende soorten vergelijkingen en zie hoe wiskunde de wereld om je heen kan verklaren.