Zijde Van Een Driehoek Berekenen

Het berekenen van de zijde van een driehoek is een fundamenteel concept in de meetkunde, met toepassingen die verder reiken dan alleen wiskundeboeken. Van architectuur tot navigatie, de principes achter deze berekeningen zijn overal om ons heen. In dit artikel duiken we diep in de verschillende methoden om een zijde van een driehoek te berekenen, waarbij we de theorie uitleggen en illustratieve voorbeelden geven.

Methoden voor het Berekenen van een Zijde

Er zijn verschillende manieren om een zijde van een driehoek te berekenen, afhankelijk van de informatie die je al hebt. De meest voorkomende methoden zijn:

De Stelling van Pythagoras

De stelling van Pythagoras is wellicht de meest bekende stelling in de meetkunde. Ze is echter alleen van toepassing op rechthoekige driehoeken. De stelling stelt dat in een rechthoekige driehoek, het kwadraat van de lengte van de schuine zijde (de zijde tegenover de rechte hoek) gelijk is aan de som van de kwadraten van de lengtes van de andere twee zijden. Wiskundig gezien: a² + b² = c², waarbij 'a' en 'b' de lengtes van de rechthoekszijden zijn en 'c' de lengte van de schuine zijde.

Voorbeeld: Stel dat je een rechthoekige driehoek hebt met rechthoekszijden van 3 cm en 4 cm. Om de lengte van de schuine zijde te berekenen, gebruik je de stelling van Pythagoras: 3² + 4² = c², wat resulteert in 9 + 16 = c², dus c² = 25. De wortel van 25 is 5, dus de lengte van de schuine zijde is 5 cm.

Trigonometrische Functies

Trigonometrische functies zoals sinus (sin), cosinus (cos) en tangens (tan) zijn uiterst handig wanneer je een hoek en de lengte van minstens één zijde kent in een rechthoekige driehoek. Deze functies definiëren de verhoudingen tussen de zijden en hoeken in de driehoek.

De definities zijn als volgt:

Sinus (sin) = Overstaande zijde / Schuine zijde
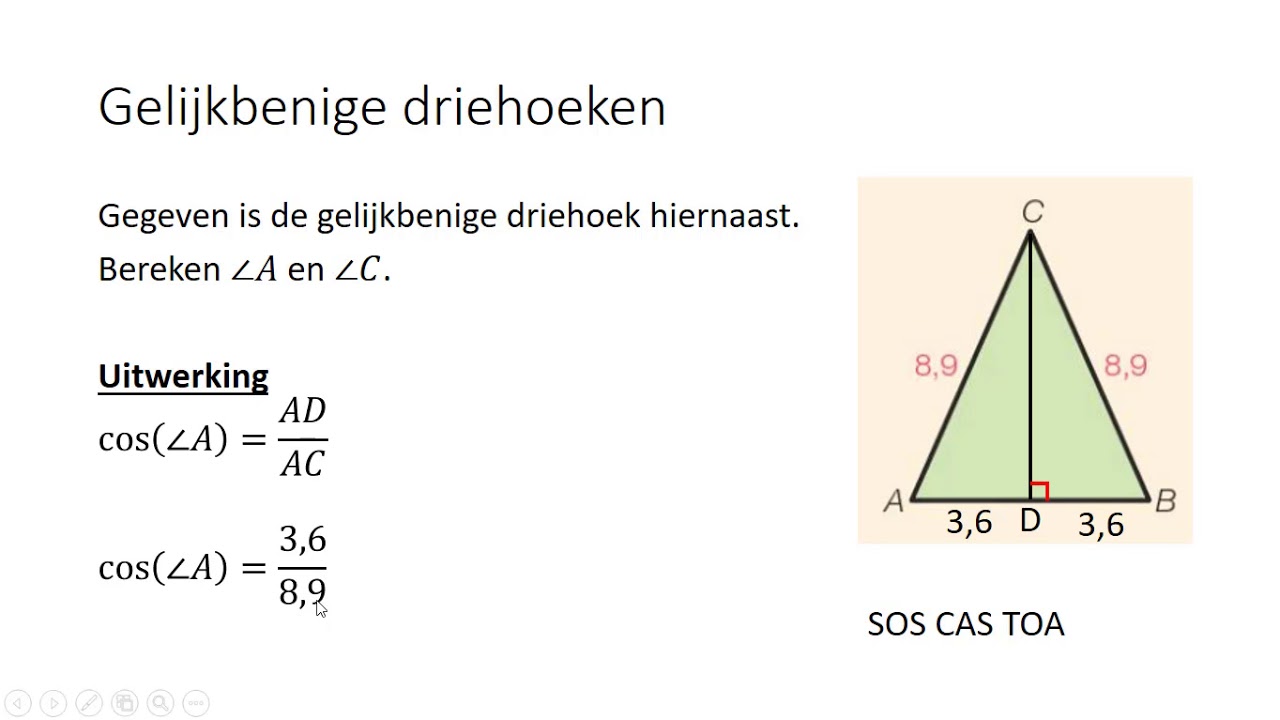
Cosinus (cos) = Aanliggende zijde / Schuine zijde
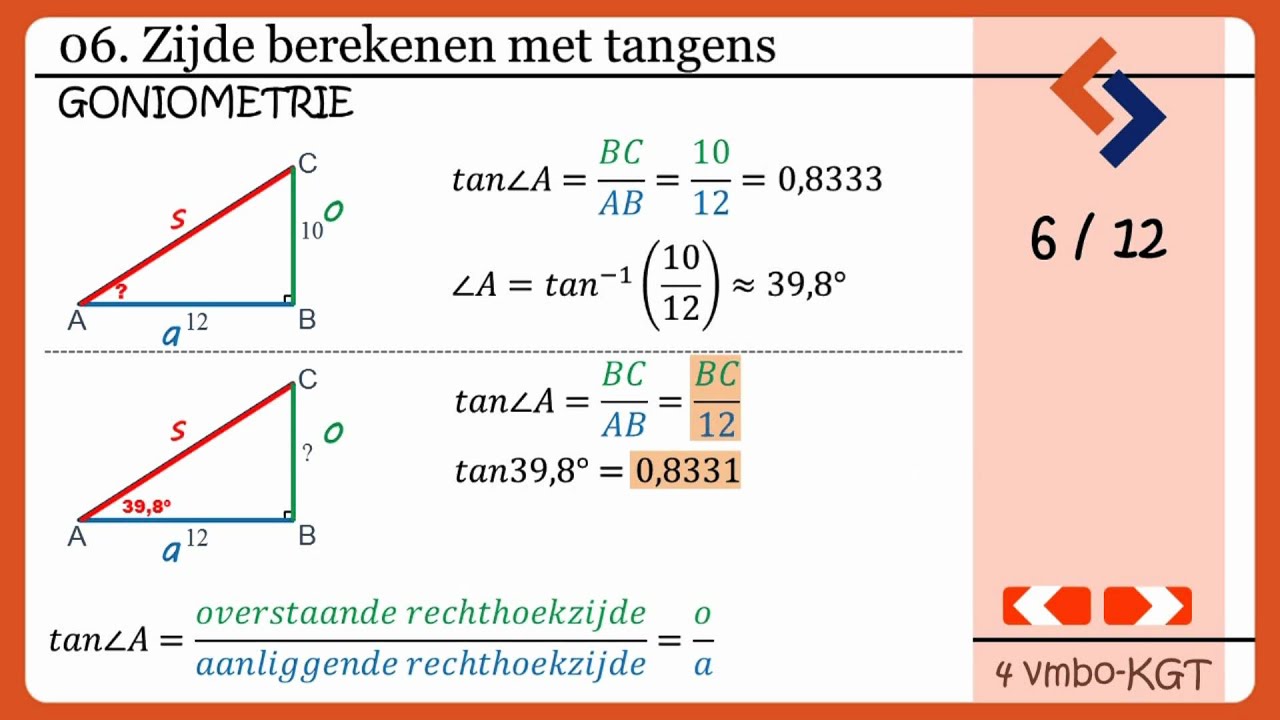
Tangens (tan) = Overstaande zijde / Aanliggende zijde

Voorbeeld: Stel dat je een rechthoekige driehoek hebt met een hoek van 30 graden en de schuine zijde is 10 cm lang. Je wilt de lengte van de overstaande zijde berekenen. Gebruik de sinusfunctie: sin(30°) = Overstaande zijde / 10. Omdat sin(30°) = 0.5, geldt: 0.5 = Overstaande zijde / 10. Dus, de overstaande zijde is 0.5 * 10 = 5 cm.

De Sinusregel

De sinusregel is bruikbaar bij niet-rechthoekige driehoeken, wanneer je twee hoeken en een zijde (HZH) kent, of twee zijden en een hoek tegenover een van die zijden (ZZH). De regel stelt dat de verhouding van de lengte van een zijde tot de sinus van de tegenoverliggende hoek constant is voor alle zijden en hoeken in de driehoek.

Wiskundig gezien: a / sin(A) = b / sin(B) = c / sin(C), waarbij a, b en c de zijden zijn en A, B en C de tegenoverliggende hoeken.

Voorbeeld: Stel dat je een driehoek hebt met zijde a = 8 cm, hoek A = 60 graden en hoek B = 45 graden. Je wilt zijde b berekenen. Gebruik de sinusregel: 8 / sin(60°) = b / sin(45°). Dus, b = (8 * sin(45°)) / sin(60°). Omdat sin(45°) ≈ 0.707 en sin(60°) ≈ 0.866, geldt: b ≈ (8 * 0.707) / 0.866 ≈ 6.53 cm.

De Cosinusregel

De cosinusregel is ook handig voor niet-rechthoekige driehoeken. Je gebruikt deze regel wanneer je drie zijden kent (ZZZ), of twee zijden en de ingesloten hoek (ZHZ). De cosinusregel verbindt de lengtes van de zijden van een driehoek met de cosinus van één van de hoeken.

Er zijn drie vormen van de cosinusregel:

a² = b² + c² - 2bc * cos(A)
b² = a² + c² - 2ac * cos(B)
c² = a² + b² - 2ab * cos(C)

Voorbeeld: Stel dat je een driehoek hebt met zijde a = 5 cm, zijde b = 7 cm en hoek C = 60 graden. Je wilt zijde c berekenen. Gebruik de cosinusregel: c² = 5² + 7² - 2 * 5 * 7 * cos(60°). Omdat cos(60°) = 0.5, geldt: c² = 25 + 49 - 35 = 39. Dus, c = √39 ≈ 6.25 cm.

Real-World Voorbeelden

De principes van driehoeksberekeningen zijn essentieel in diverse vakgebieden:

Architectuur: Architecten gebruiken trigonometrie om hoeken en afstanden in gebouwen te berekenen, bijvoorbeeld bij het ontwerpen van daken en bruggen.
Navigatie: Piloten en zeelieden gebruiken trigonometrie en de sinus- en cosinusregels voor positiebepaling en het uitzetten van routes. GPS-systemen vertrouwen sterk op deze wiskundige principes.
Landmeten: Landmeters gebruiken driehoeksmeting (triangulatie) om afstanden en hoogtes te bepalen, bijvoorbeeld bij het uitzetten van landkaarten en het bepalen van eigendomsgrenzen.
Engineering: Ingenieurs gebruiken deze berekeningen om structuren te ontwerpen die bestand zijn tegen krachten en spanningen, denk aan bruggen, torens en gebouwen.
Astronomie: Astronomen gebruiken trigonometrie om de afstanden tot sterren te berekenen, een techniek die bekend staat als parallax.

Voorbeeld data: Stel een architect ontwerpt een dak met een hellingshoek van 35 graden. De horizontale afstand van de muur tot het hoogste punt van het dak (de "aanliggende zijde") is 8 meter. Om de lengte van de daksparren (de "schuine zijde") te berekenen, kan hij de cosinus gebruiken: cos(35°) = 8 / Schuine zijde. De schuine zijde is dan 8 / cos(35°) ≈ 8 / 0.819 ≈ 9.77 meter. Dit geeft de architect de benodigde informatie om de lengte van de daksparren te bepalen en het dak correct te construeren.

Belang van Nauwkeurigheid

Bij het berekenen van zijden van een driehoek is nauwkeurigheid van cruciaal belang. Kleine meetfouten of afrondingen kunnen leiden tot aanzienlijke verschillen in het eindresultaat, vooral bij grotere constructies of complexe berekeningen. Het is daarom belangrijk om:

Nauwkeurige metingen te verrichten: Gebruik precisie-instrumenten en herhaal metingen om de kans op fouten te minimaliseren.
Rekening te houden met significantie: Houd een consistent aantal significante cijfers aan in je berekeningen om afrondingsfouten te voorkomen.
De juiste formules te gebruiken: Zorg ervoor dat je de juiste formule selecteert op basis van de beschikbare informatie en het type driehoek (rechthoekig of niet-rechthoekig).

Het gebruik van een wetenschappelijke rekenmachine of software voor geometrische berekeningen kan ook de nauwkeurigheid verbeteren en het risico op menselijke fouten verminderen.

Conclusie en Oproep tot Actie

Het berekenen van de zijde van een driehoek is een essentiële vaardigheid met talloze toepassingen in de praktijk. Of je nu een student bent die meetkunde studeert, een professional die werkt aan een bouwproject, of gewoon iemand die geïnteresseerd is in wiskunde, het beheersen van deze technieken is ongelooflijk waardevol.

Oefening baart kunst! Probeer de methoden die we in dit artikel hebben besproken zelf toe te passen op verschillende voorbeelden. Zoek online naar oefenopgaven of creëer je eigen scenario's. Hoe meer je oefent, hoe beter je de principes zult begrijpen en hoe zelfverzekerder je zult zijn in het toepassen ervan.

Daag jezelf uit om complexere problemen op te lossen en te onderzoeken hoe deze wiskundige principes in de echte wereld worden gebruikt. De mogelijkheden zijn eindeloos, en de kennis die je opdoet zal je horizon verbreden en je probleemoplossende vaardigheden verbeteren.