Zijden Berekenen In Een Driehoek

Heb je je ooit afgevraagd hoe je de lengte van een zijde van een driehoek kunt berekenen, zelfs als je niet alle informatie hebt? Of je nu een student bent die worstelt met geometrie, een hobbyist die aan een project werkt, of gewoon nieuwsgierig bent naar de wiskunde achter de wereld om je heen, dit artikel is voor jou. We duiken in de verschillende methoden en formules die je kunt gebruiken om zijden te berekenen in een driehoek, en we zorgen ervoor dat het allemaal begrijpelijk en toepasbaar is.

Waarom Zijden Berekenen in een Driehoek Belangrijk is

Het berekenen van zijden in een driehoek is een fundamenteel concept in de wiskunde met praktische toepassingen in diverse velden. Denk aan:

• Architectuur en Constructie: Het bepalen van de afmetingen van daken, bruggen, en andere structuren.
• Navigatie: Het berekenen van afstanden en richtingen.
• Engineering: Het ontwerpen van machines en structuren die aan bepaalde eisen voldoen.
• Grafisch Ontwerp en Gaming: Het creëren van realistische 3D-modellen en omgevingen.

Kortom, de vaardigheid om zijden in een driehoek te berekenen is een waardevolle tool in veel verschillende contexten.

De Basis: Soorten Driehoeken

Voordat we in de methoden duiken, is het belangrijk om de verschillende soorten driehoeken te kennen. Dit helpt ons bepalen welke technieken het meest geschikt zijn.

• Gelijkzijdige Driehoek: Alle drie zijden zijn even lang en alle drie hoeken zijn 60 graden.
• Gelijkbenige Driehoek: Twee zijden zijn even lang en de hoeken tegenover die zijden zijn gelijk.
• Ongelijkzijdige Driehoek: Alle drie zijden zijn verschillend en alle drie hoeken zijn verschillend.
• Rechthoekige Driehoek: Bevat één rechte hoek (90 graden). De zijde tegenover de rechte hoek wordt de hypotenusa genoemd.
• Scherphoekige Driehoek: Alle drie hoeken zijn kleiner dan 90 graden.
• Stomphoekige Driehoek: Bevat één hoek groter dan 90 graden.

Methoden voor het Berekenen van Zijden

Nu komen we bij de kern van de zaak: hoe berekenen we die zijden? Hier zijn de belangrijkste methoden:

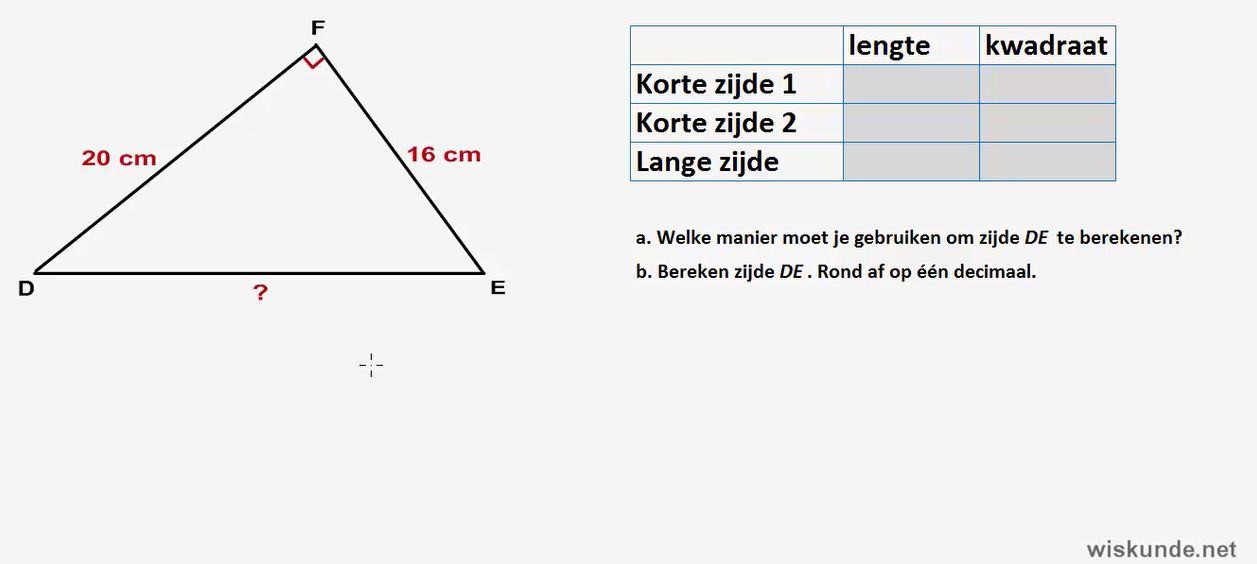
1. De Stelling van Pythagoras

De stelling van Pythagoras is een van de meest bekende stellingen in de wiskunde. Hij is alleen van toepassing op rechthoekige driehoeken.

De formule luidt: a² + b² = c²

• a en b zijn de lengtes van de rechthoekszijden (de zijden die de rechte hoek vormen).
• c is de lengte van de hypotenusa (de zijde tegenover de rechte hoek).

Voorbeeld: Stel dat je een rechthoekige driehoek hebt met een zijde van 3 cm en een zijde van 4 cm. Wat is de lengte van de hypotenusa?

Oplossing:

a² + b² = c²

3² + 4² = c²

9 + 16 = c²

25 = c²

c = √25 = 5 cm

De lengte van de hypotenusa is 5 cm.

2. Goniometrische Functies (Sinus, Cosinus, Tangens)

Goniometrische functies, ook wel trigonometrische functies genoemd, worden gebruikt om de verhouding tussen de hoeken en zijden van een rechthoekige driehoek te bepalen. De drie belangrijkste functies zijn:

• Sinus (sin): sin(hoek) = Overstaande zijde / Hypotenusa
• Cosinus (cos): cos(hoek) = Aanliggende zijde / Hypotenusa
• Tangens (tan): tan(hoek) = Overstaande zijde / Aanliggende zijde

Ezelsbruggetje: SOS CAS TOA (Sinus = Overstaand / Hypotenusa, Cosinus = Aanliggend / Hypotenusa, Tangens = Overstaand / Aanliggend)

Voorbeeld: Stel dat je een rechthoekige driehoek hebt met een hoek van 30 graden en een hypotenusa van 10 cm. Wat is de lengte van de overstaande zijde?

Oplossing:

sin(30°) = Overstaande zijde / 10 cm

Overstaande zijde = sin(30°) * 10 cm

Overstaande zijde = 0.5 * 10 cm = 5 cm

De lengte van de overstaande zijde is 5 cm.

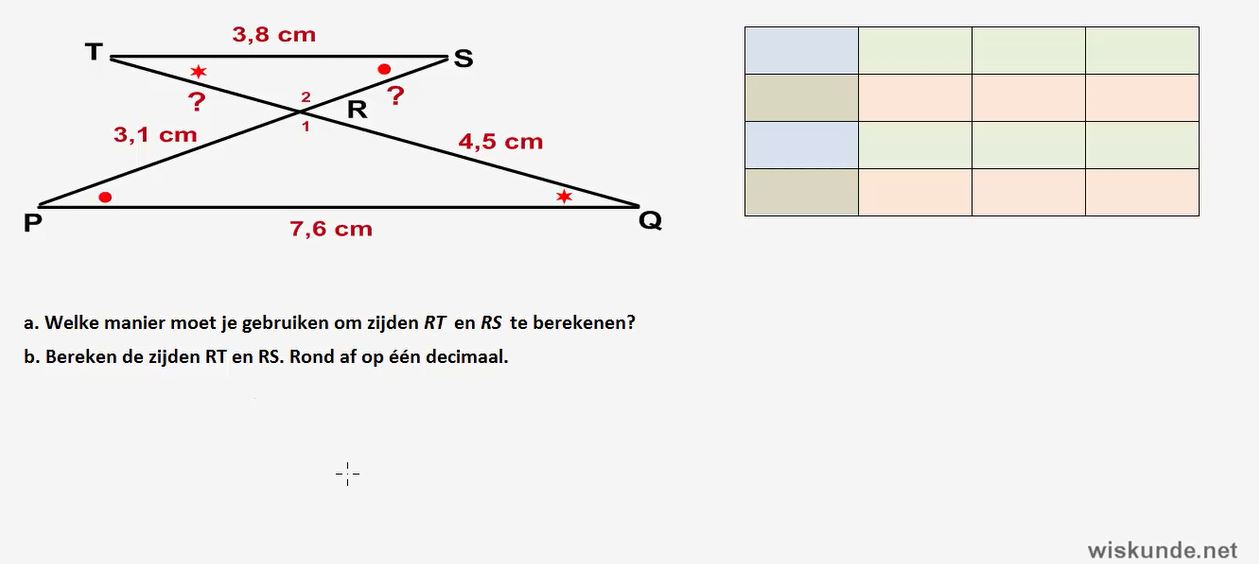
3. De Sinusregel

De sinusregel is handig als je geen rechthoekige driehoek hebt, maar wel de lengte van één zijde en de grootte van de tegenoverliggende hoek kent, en de grootte van een andere hoek.

De formule luidt: a / sin(A) = b / sin(B) = c / sin(C)

• a, b en c zijn de lengtes van de zijden.
• A, B en C zijn de hoeken tegenover de respectievelijke zijden.

Voorbeeld: Stel dat je een driehoek hebt met zijde a = 8 cm, hoek A = 60 graden en hoek B = 45 graden. Wat is de lengte van zijde b?

Oplossing:

a / sin(A) = b / sin(B)

8 cm / sin(60°) = b / sin(45°)

b = (8 cm * sin(45°)) / sin(60°)

b = (8 cm * 0.707) / 0.866

b ≈ 6.53 cm

De lengte van zijde b is ongeveer 6.53 cm.

4. De Cosinusregel

De cosinusregel is een andere krachtige tool die je kunt gebruiken wanneer je geen rechthoekige driehoek hebt. Je gebruikt het als je de lengtes van twee zijden kent en de grootte van de hoek die ze insluiten, of als je de lengtes van alle drie de zijden kent.

De formules luiden:

• a² = b² + c² - 2bc * cos(A)
• b² = a² + c² - 2ac * cos(B)
• c² = a² + b² - 2ab * cos(C)

• a, b en c zijn de lengtes van de zijden.
• A, B en C zijn de hoeken tegenover de respectievelijke zijden.

Voorbeeld: Stel dat je een driehoek hebt met zijde a = 5 cm, zijde b = 7 cm en hoek C = 60 graden. Wat is de lengte van zijde c?

Oplossing:

c² = a² + b² - 2ab * cos(C)

c² = 5² + 7² - 2 * 5 * 7 * cos(60°)

c² = 25 + 49 - 70 * 0.5

c² = 74 - 35

c² = 39

c = √39 ≈ 6.25 cm

De lengte van zijde c is ongeveer 6.25 cm.

Tips en Trucs

• Schets de Driehoek: Maak altijd een schets van de driehoek om de informatie te visualiseren en te bepalen welke methode het meest geschikt is.
• Controleer je Antwoord: Zorg ervoor dat je antwoord logisch is. De langste zijde moet tegenover de grootste hoek liggen, enzovoort.
• Gebruik een Rekenmachine: Gebruik een rekenmachine met trigonometrische functies voor nauwkeurige berekeningen.
• Oefening Baart Kunst: Hoe meer je oefent met het berekenen van zijden in driehoeken, hoe beter je erin wordt.

Conclusie

Het berekenen van zijden in een driehoek is een essentiële vaardigheid met toepassingen in verschillende vakgebieden. Door de verschillende soorten driehoeken te begrijpen en de juiste methoden (Pythagoras, sinus, cosinus, sinusregel, cosinusregel) te gebruiken, kun je elk zijdeprobleem oplossen. Onthoud dat oefening cruciaal is. Dus pak je rekenmachine, pak een paar voorbeelden en begin met het verkennen van de wondere wereld van driehoeksberekeningen! Met een beetje oefening zul je merken dat je zelfverzekerd en competent bent in het oplossen van deze problemen.