Zijden Van Een Driehoek Berekenen

Weet je dat moment, dat je naar een gebouw kijkt, een meubel in elkaar probeert te zetten, of zelfs een kunstwerk bewondert, en je je afvraagt hoe die vormen en hoeken eigenlijk berekend zijn? Veel van die berekeningen komen neer op het begrijpen van driehoeken en de relatie tussen hun zijden.

Het berekenen van de zijden van een driehoek kan in eerste instantie intimiderend lijken, zeker als wiskunde niet je favoriete vak was op school. Maar maak je geen zorgen, het is echt niet zo ingewikkeld als je misschien denkt. We gaan het stap voor stap uitleggen, zodat je straks zelfverzekerd aan de slag kunt met deze basisvaardigheid.

Waarom is dit belangrijk? Het gaat verder dan alleen schoolse wiskunde. Stel je voor: je bent een architect die een dakconstructie ontwerpt, een timmerman die een schap in elkaar zet, of zelfs een programmeur die games maakt met 3D-graphics. In al deze gevallen (en nog veel meer!) is het berekenen van de zijden van een driehoek essentieel. Zonder deze kennis kun je letterlijk en figuurlijk in de problemen komen.

Basiskennis: Wat is een driehoek?

Laten we beginnen met de basis. Een driehoek is een figuur met drie zijden en drie hoeken. De som van de hoeken in een driehoek is altijd 180 graden. Er zijn verschillende soorten driehoeken, elk met hun eigen eigenschappen:

• Gelijkzijdige driehoek: Alle drie de zijden zijn even lang en alle drie de hoeken zijn 60 graden.
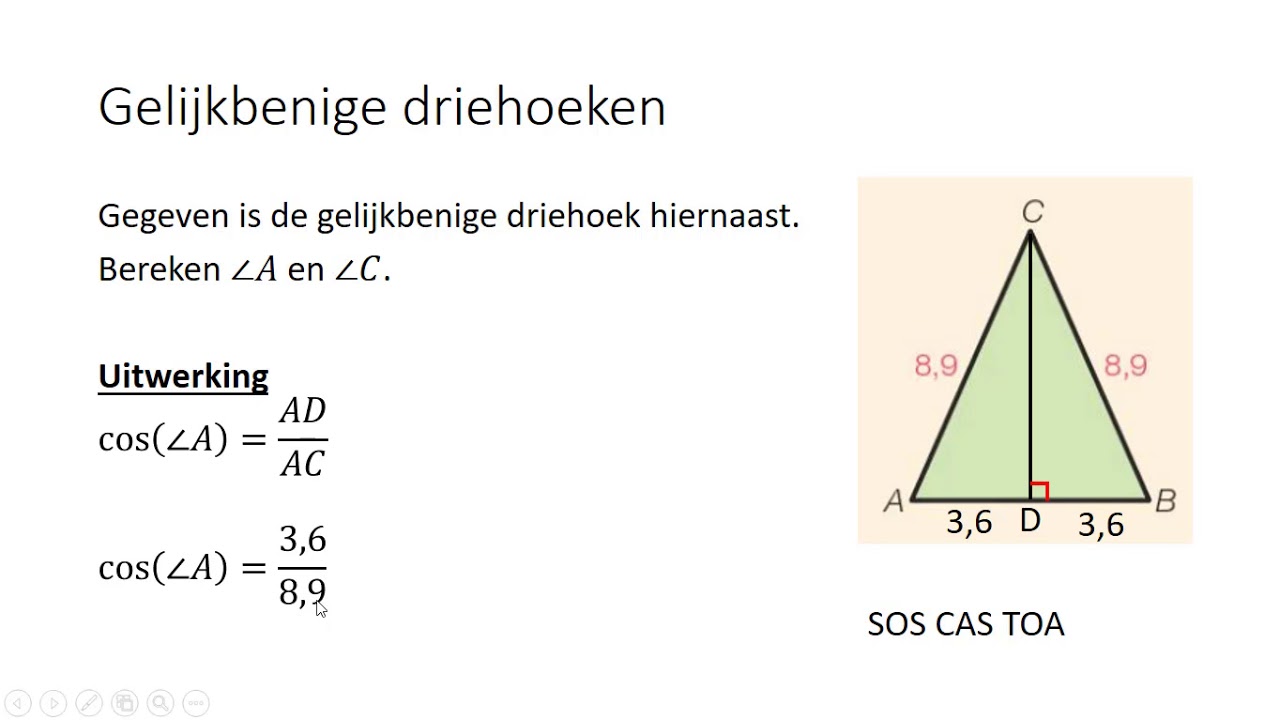
• Gelijkbenige driehoek: Twee zijden zijn even lang en de hoeken tegenover die zijden zijn gelijk.
• Ongelijkzijdige driehoek: Alle drie de zijden zijn verschillend en alle drie de hoeken zijn verschillend.
• Rechthoekige driehoek: Eén van de hoeken is 90 graden (een rechte hoek). De zijde tegenover de rechte hoek noemen we de hypotenusa. De andere twee zijden zijn de rechthoekszijden.

De rechthoekige driehoek is in het bijzonder belangrijk, omdat we hier de stelling van Pythagoras kunnen gebruiken.

De Stelling van Pythagoras

De stelling van Pythagoras is een fundamentele formule die de relatie beschrijft tussen de zijden van een rechthoekige driehoek. De stelling luidt:

a² + b² = c²

Waar:

• a en b de lengtes zijn van de rechthoekszijden.
• c de lengte is van de hypotenusa (de zijde tegenover de rechte hoek).

Voorbeeld: Stel dat je een rechthoekige driehoek hebt met rechthoekszijden van 3 cm en 4 cm. Hoe lang is de hypotenusa?

1. Gebruik de formule: a² + b² = c²
2. Vul de bekende waarden in: 3² + 4² = c²
3. Bereken: 9 + 16 = c²
4. Vereenvoudig: 25 = c²
5. Neem de wortel van beide zijden: c = √25 = 5

De hypotenusa is dus 5 cm lang.

Wanneer kun je Pythagoras *niet* gebruiken?

Het is cruciaal om te onthouden dat de stelling van Pythagoras alleen geldig is voor rechthoekige driehoeken. Als de driehoek geen rechte hoek heeft, moet je andere methoden gebruiken, zoals de sinus- en cosinusregel (die we later zullen bespreken).

Sinus, Cosinus en Tangens (Trigonometrie)

Voor driehoeken die niet rechthoekig zijn, hebben we trigonometrie nodig. De belangrijkste trigonometrische functies zijn sinus (sin), cosinus (cos) en tangens (tan). Deze functies beschrijven de verhouding tussen de zijden van een rechthoekige driehoek en de hoeken. Onthoud dat ook deze functies *alleen* direct bruikbaar zijn voor rechthoekige driehoeken. We gebruiken ze als bouwstenen voor de sinus- en cosinusregel bij niet-rechthoekige driehoeken.

Laten we eens kijken naar een rechthoekige driehoek met een hoek θ (theta):

• Sinus (sin): De verhouding van de overstaande zijde (de zijde tegenover de hoek θ) tot de hypotenusa. Dus: sin(θ) = Overstaand / Hypotenusa
• Cosinus (cos): De verhouding van de aanliggende zijde (de zijde die aan de hoek θ ligt, maar niet de hypotenusa) tot de hypotenusa. Dus: cos(θ) = Aanliggend / Hypotenusa
• Tangens (tan): De verhouding van de overstaande zijde tot de aanliggende zijde. Dus: tan(θ) = Overstaand / Aanliggend

Een handig ezelsbruggetje om deze te onthouden is: SOS CAS TOA (Sinus = Overstaand / Hypotenusa, Cosinus = Aanliggend / Hypotenusa, Tangens = Overstaand / Aanliggend).

Hoe gebruik je Sinus, Cosinus en Tangens?

Stel, je hebt een rechthoekige driehoek met een hoek van 30 graden en een hypotenusa van 10 cm. Je wilt de lengte van de overstaande zijde weten.

1. We weten de hoek (30 graden) en de hypotenusa (10 cm), en we willen de overstaande zijde weten. Dus we gebruiken de sinusfunctie: sin(θ) = Overstaand / Hypotenusa
2. Vul de bekende waarden in: sin(30°) = Overstaand / 10
3. Zoek de waarde van sin(30°) op (of gebruik een rekenmachine): sin(30°) = 0.5
4. Dus: 0.5 = Overstaand / 10
5. Vermenigvuldig beide zijden met 10: Overstaand = 0.5 * 10 = 5

De overstaande zijde is dus 5 cm lang.

De Sinusregel en Cosinusregel

Voor driehoeken die *niet* rechthoekig zijn, hebben we de sinusregel en de cosinusregel nodig. Deze regels zijn krachtige hulpmiddelen om de zijden en hoeken van elke driehoek te berekenen, zolang je maar voldoende informatie hebt (bijvoorbeeld twee zijden en een hoek, of twee hoeken en een zijde).

De Sinusregel

De sinusregel stelt dat de verhouding tussen de lengte van een zijde en de sinus van de tegenoverliggende hoek constant is voor alle zijden en hoeken in een driehoek. In formulevorm:

a / sin(A) = b / sin(B) = c / sin(C)

Waar:

• a, b en c de lengtes zijn van de zijden van de driehoek.
• A, B en C de hoeken zijn tegenover de zijden a, b en c respectievelijk.

De Cosinusregel

De cosinusregel is een algemene formule die een relatie legt tussen de lengte van één zijde van een driehoek en de lengtes van de andere twee zijden en de cosinus van de hoek tussen die twee zijden. Er zijn drie varianten van de cosinusregel, afhankelijk van welke zijde je wilt berekenen:

• a² = b² + c² - 2bc * cos(A)
• b² = a² + c² - 2ac * cos(B)
• c² = a² + b² - 2ab * cos(C)

Waar:

• a, b en c de lengtes zijn van de zijden van de driehoek.
• A, B en C de hoeken zijn tegenover de zijden a, b en c respectievelijk.

Wanneer gebruik je de Sinusregel en wanneer de Cosinusregel?

• Sinusregel: Gebruik de sinusregel als je twee hoeken en één zijde kent (AAS of ASA), of als je twee zijden en de hoek tegenover één van die zijden kent (SSA). Let op: de SSA-situatie kan soms tot twee mogelijke oplossingen leiden (de zogenaamde "ambigue case").
• Cosinusregel: Gebruik de cosinusregel als je drie zijden kent (SSS), of als je twee zijden en de hoek daartussen kent (SAS).

Praktische Voorbeelden

Laten we een paar praktische voorbeelden bekijken om te zien hoe we deze regels in de praktijk kunnen toepassen.

Voorbeeld 1: Je bent een landmeter en je wilt de afstand meten over een rivier. Je meet een hoek van 60 graden vanaf punt A naar een boom aan de overkant (punt C). Je loopt 50 meter langs de oever naar punt B en meet daar een hoek van 80 graden naar dezelfde boom (punt C). Hoe breed is de rivier (de afstand van punt A naar punt C)?

1. We hebben een driehoek ABC, waarbij we AB = 50 meter, hoek A = 60 graden en hoek B = 80 graden kennen.
2. We kunnen hoek C berekenen: hoek C = 180 - 60 - 80 = 40 graden.
3. We willen de zijde AC weten. We gebruiken de sinusregel: AC / sin(B) = AB / sin(C)
4. Vul de bekende waarden in: AC / sin(80°) = 50 / sin(40°)
5. Bereken: AC = (50 * sin(80°)) / sin(40°) ≈ 76.6 meter

De rivier is dus ongeveer 76.6 meter breed.

Voorbeeld 2: Je bent een architect en je ontwerpt een driehoekig raam. Je weet dat de zijden van het raam 2 meter, 3 meter en 4 meter lang moeten zijn. Onder welke hoeken moeten de hoeken van het raam gezaagd worden?

1. We hebben een driehoek met zijden a = 2, b = 3 en c = 4. We willen de hoeken A, B en C weten.
2. We gebruiken de cosinusregel om bijvoorbeeld hoek A te berekenen: a² = b² + c² - 2bc * cos(A)
3. Vul de bekende waarden in: 2² = 3² + 4² - 2 * 3 * 4 * cos(A)
4. Vereenvoudig: 4 = 9 + 16 - 24 * cos(A)
5. Vereenvoudig verder: -21 = -24 * cos(A)
6. Bereken cos(A): cos(A) = 21 / 24 = 0.875
7. Bereken hoek A: A = arccos(0.875) ≈ 28.96 graden
8. Herhaal dit proces voor de andere hoeken B en C, of gebruik de sinusregel nadat je één hoek hebt berekend.

Belangrijke Aandachtspunten en Counterpoints

Het is belangrijk om te beseffen dat deze berekeningen gebaseerd zijn op ideale driehoeken. In de praktijk kunnen er kleine afwijkingen zijn door meetfouten of imperfecties in de materialen. Het is dus belangrijk om altijd een marge aan te houden.

Soms hoor je mensen zeggen: "Ik heb dit toch nooit nodig in mijn leven!". En dat is misschien waar, als je een kantoorbaan hebt en nooit met constructies of ontwerpen te maken krijgt. Maar zelfs dan kan het nuttig zijn om logisch te leren denken en problemen op te lossen. En voor degenen die wél in de bouw, techniek of design werken, is deze kennis onmisbaar.

Conclusie

Het berekenen van de zijden van een driehoek is een fundamentele vaardigheid die in veel verschillende vakgebieden van pas komt. Of je nu een architect, een timmerman, een programmeur of gewoon een nieuwsgierige denker bent, het begrijpen van de stelling van Pythagoras, de trigonometrische functies en de sinus- en cosinusregel kan je helpen om problemen op te lossen en de wereld om je heen beter te begrijpen.

We hebben gezien dat er verschillende manieren zijn om de zijden van een driehoek te berekenen, afhankelijk van de informatie die je hebt. Onthoud dat de stelling van Pythagoras alleen geldt voor rechthoekige driehoeken, en dat je voor niet-rechthoekige driehoeken de sinus- en cosinusregel nodig hebt.

Ben je klaar om je nieuwe kennis in de praktijk te brengen en een eigen driehoekig project te starten? Wat ga jij nu berekenen?