Bereken Omtrek Van Een Cirkel

De omtrek van een cirkel is een fundamenteel concept in de meetkunde en heeft talloze praktische toepassingen in het dagelijks leven. Of je nu een pizza bakt, een wiel ontwerpt of de omtrek van een planetair stelsel berekent, het begrijpen van hoe je de omtrek van een cirkel kunt bepalen is cruciaal. Dit artikel duikt diep in de wereld van cirkels, leggen de basisprincipes uit en illustreren de relevantie ervan met praktische voorbeelden.

De Basis: Definities en Formules

Voordat we in de berekening duiken, is het belangrijk om de basisdefinities te kennen:

Cirkel: Een tweedimensionale geometrische figuur die bestaat uit alle punten die zich op dezelfde afstand bevinden van een centraal punt.
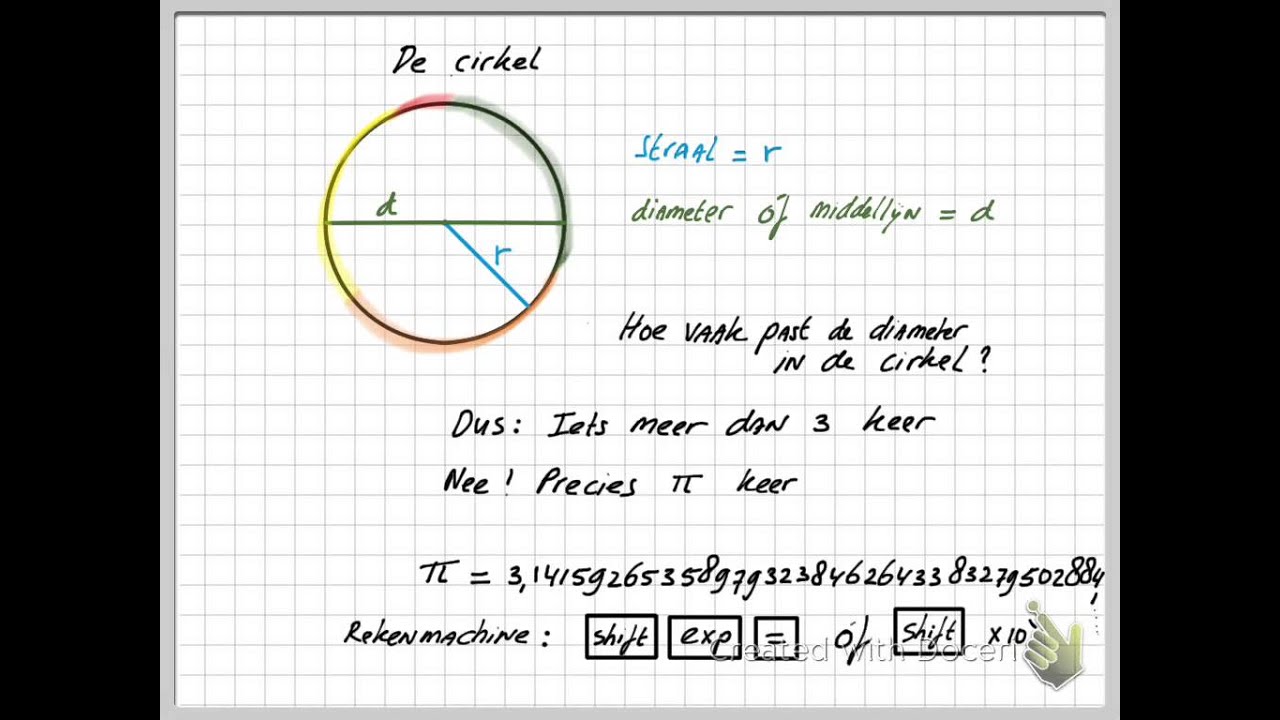
Straal (r): De afstand van het middelpunt van de cirkel tot elk punt op de omtrek.
Diameter (d): Een lijnstuk dat door het middelpunt van de cirkel loopt en de omtrek in twee punten raakt. De diameter is twee keer zo lang als de straal (d = 2r).
Omtrek (C): De totale afstand rondom de cirkel. Dit is wat we willen berekenen.

De formule voor de omtrek van een cirkel is relatief eenvoudig:

C = πd of C = 2πr

Waarbij:

C staat voor de omtrek
π (pi) is een wiskundige constante, ongeveer gelijk aan 3,14159
d staat voor de diameter
r staat voor de straal

Pi (π): Een Cruciaal Getal

Het getal π is een irrationeel getal, wat betekent dat het een oneindige, niet-repeterende decimale uitbreiding heeft. Ondanks dat we meestal een afgeronde waarde van 3,14 of 3,14159 gebruiken, is het belangrijk te onthouden dat dit slechts een benadering is. De werkelijke waarde van π is oneindig. De precisie die nodig is voor π hangt af van de specifieke toepassing; voor alledaagse berekeningen is 3,14 vaak voldoende, terwijl wetenschappelijke en technische toepassingen een hogere precisie vereisen.

De Berekening in de Praktijk

Laten we een paar voorbeelden bekijken om te illustreren hoe je de omtrek van een cirkel berekent:

Voorbeeld 1: Bekende Straal

Stel dat we een cirkel hebben met een straal van 5 cm. Om de omtrek te berekenen, gebruiken we de formule C = 2πr:

C = 2 * 3,14159 * 5 cm

C ≈ 31,4159 cm

Dus de omtrek van de cirkel is ongeveer 31,4159 cm.

Voorbeeld 2: Bekende Diameter

Stel dat we een cirkel hebben met een diameter van 12 meter. Om de omtrek te berekenen, gebruiken we de formule C = πd:

C = 3,14159 * 12 m

C ≈ 37,6991 m

Dus de omtrek van de cirkel is ongeveer 37,6991 meter.

Voorbeeld 3: Een Samengestelde Berekening

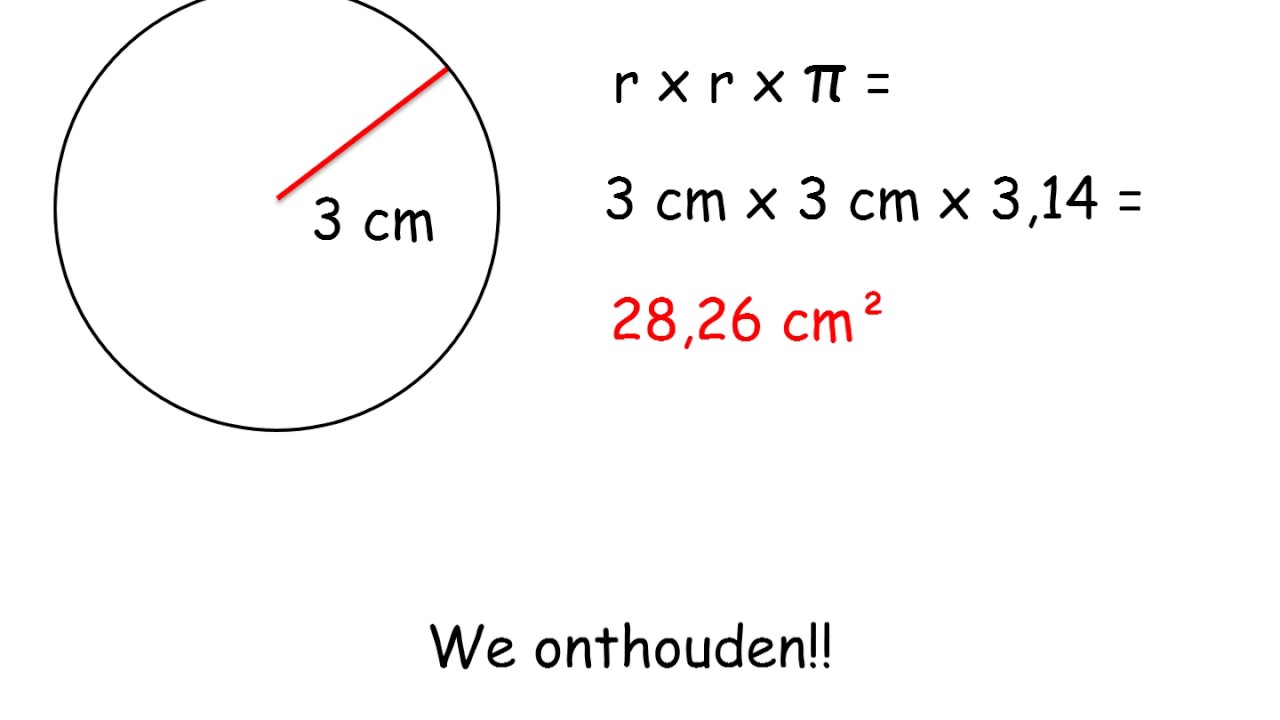
Wat als we een cirkel hebben waarvan we alleen de oppervlakte weten? Stel de oppervlakte is 50 cm². We moeten eerst de straal berekenen met de formule voor de oppervlakte van een cirkel: A = πr².

50 = πr²

r² = 50 / π

r² ≈ 50 / 3.14159

r² ≈ 15.9155

r ≈ √15.9155

r ≈ 3.99 cm

Nu we de straal hebben, kunnen we de omtrek berekenen:

C = 2πr

C = 2 * 3.14159 * 3.99 cm

C ≈ 25.07 cm

Dus de omtrek van de cirkel is ongeveer 25.07 cm.

Real-World Toepassingen

De berekening van de omtrek van een cirkel is niet alleen een theoretische oefening. Het heeft vele praktische toepassingen in verschillende industrieën en het dagelijks leven.

Engineering en Constructie

In de engineering wordt de omtrek van een cirkel gebruikt bij het ontwerpen van wielen, tandwielen, buizen en andere ronde objecten. Architecten gebruiken het om de lengte van een rond gebouw of een sierlijke koepel te bepalen. Bij de constructie van bruggen en tunnels is nauwkeurige meting van cirkelvormige componenten essentieel voor veiligheid en stabiliteit.

Productie

Bij de productie wordt de omtrek berekend voor het bepalen van de benodigde hoeveelheid materiaal om een cirkelvormig product te maken, zoals een pizza, een taart of een metalen plaat. Het is ook cruciaal bij het afsnijden van stoffen voor ronde objecten, zoals tenten of koepels.

Transport

In de transportsector is de omtrek van een wiel direct gerelateerd aan de afstand die een voertuig aflegt per omwenteling van het wiel. Dit is belangrijk voor het kalibreren van snelheidsmeters en het berekenen van afstanden. Denk aan fietsen: de wielomtrek bepaalt hoeveel meter je aflegt per pedaalslag.

Astronomie

Zelfs in de astronomie wordt de omtrek gebruikt om de omtrek van hemellichamen, zoals planeten en sterren, te schatten. Hoewel we ze niet direct kunnen meten, kunnen we hun straal (of diameter) bepalen via telescopen en vervolgens de omtrek berekenen.

Dagelijks Leven

In het dagelijks leven gebruiken we de omtrek onbewust vaak. Bijvoorbeeld, als je een touw rond een ronde tafel wilt knopen, moet je de omtrek van de tafel schatten. Of wanneer je een pizza bakt en je wilt weten hoeveel korst je nodig hebt.

Veelgemaakte Fouten en Hoe Ze Te Vermijden

Bij het berekenen van de omtrek van een cirkel zijn er een paar veelgemaakte fouten die je kunt vermijden:

Verwarring tussen straal en diameter: Zorg ervoor dat je de juiste waarde gebruikt in de formule. De diameter is twee keer zo lang als de straal.
Verkeerde waarde van π: Gebruik altijd een nauwkeurige waarde van π, afhankelijk van de precisie die je nodig hebt. 3,14 is een goede benadering, maar 3,14159 is nauwkeuriger.
Vergeten de eenheden te vermelden: Vergeet niet om de juiste eenheden te vermelden (bijvoorbeeld cm, meter, km) in je antwoord.
Rondingsfouten: Vermijd afrondingsfouten door pas aan het einde van de berekening af te ronden.

Tools en Hulpbronnen

Er zijn verschillende tools en hulpmiddelen beschikbaar om je te helpen bij het berekenen van de omtrek van een cirkel:

Rekenmachines: Online rekenmachines en wetenschappelijke rekenmachines kunnen de omtrek snel en nauwkeurig berekenen.
Spreadsheets: Programma's zoals Excel of Google Sheets kunnen worden gebruikt om de formule in te voeren en de omtrek automatisch te berekenen.
Apps: Er zijn talloze mobiele apps beschikbaar die speciaal zijn ontworpen voor geometrische berekeningen.

Conclusie

De omtrek van een cirkel is een fundamenteel concept met brede toepassingen. Door de basisdefinities, de formules en de praktische voorbeelden te begrijpen, kun je de omtrek van een cirkel met vertrouwen berekenen. Of je nu een student bent, een ingenieur, een architect of gewoon iemand die geïnteresseerd is in wiskunde, het beheersen van dit concept is essentieel. Gebruik de tools en hulpmiddelen die beschikbaar zijn om je te helpen en vermijd de veelgemaakte fouten. Ga aan de slag en ontdek de cirkelvormige wereld om je heen!