Berekening Omtrek Van Een Cirkel

Heb je ooit moeite gehad met het berekenen van de omtrek van een cirkel? Misschien zit je vast aan een wiskundehuiswerkopdracht, of ben je bezig met een DIY-project waarbij je precies de juiste lengte van materialen nodig hebt. Wat de reden ook is, je bent niet de enige. Veel mensen vinden het lastig, maar geloof me, het is eenvoudiger dan je denkt! Dit artikel is er om je stap voor stap door het proces te leiden, zodat je straks met vertrouwen de omtrek van elke cirkel kunt berekenen.

Wat is de Omtrek van een Cirkel?

De omtrek van een cirkel is eigenlijk niets meer dan de lengte van de buitenste rand. Stel je voor dat je een touwtje om een pizzabodem legt; de lengte van dat touwtje is de omtrek. Het is een fundamenteel concept in de meetkunde, en het begrijpen ervan opent deuren naar een breed scala aan toepassingen in de echte wereld.

Waarom is het Belangrijk?

Je vraagt je misschien af: "Waarom zou ik me hier druk om maken?" Nou, het berekenen van de omtrek van een cirkel is verrassend handig. Denk aan:

• Constructie: Architecten en ingenieurs gebruiken het om de hoeveelheid materialen te berekenen die nodig zijn voor ronde structuren.
• Fabricage: Bij het ontwerpen en produceren van wielen, buizen, en andere ronde objecten is het essentieel.
• Alledaagse situaties: Van het bepalen van de lengte van een hek om een ronde tuin tot het inschatten van de benodigde hoeveelheid lint om een taartdoos.

Zoals Dr. Math in zijn publicatie "The Joy of Pi" (fictieve titel) zegt: "Het begrijpen van basisgeometrische principes, zoals de omtrek van een cirkel, stelt ons in staat om de wereld om ons heen beter te begrijpen en problemen effectiever op te lossen."

De Formule voor de Omtrek

De omtrek van een cirkel wordt berekend met behulp van een simpele en elegante formule:

Omtrek = 2 * π * r

Laten we deze formule eens ontleden:

• Omtrek: Dit is de lengte die we proberen te vinden.
• π (Pi): Dit is een wiskundige constante, ongeveer gelijk aan 3.14159. Voor de meeste berekeningen is 3.14 een voldoende nauwkeurige benadering.
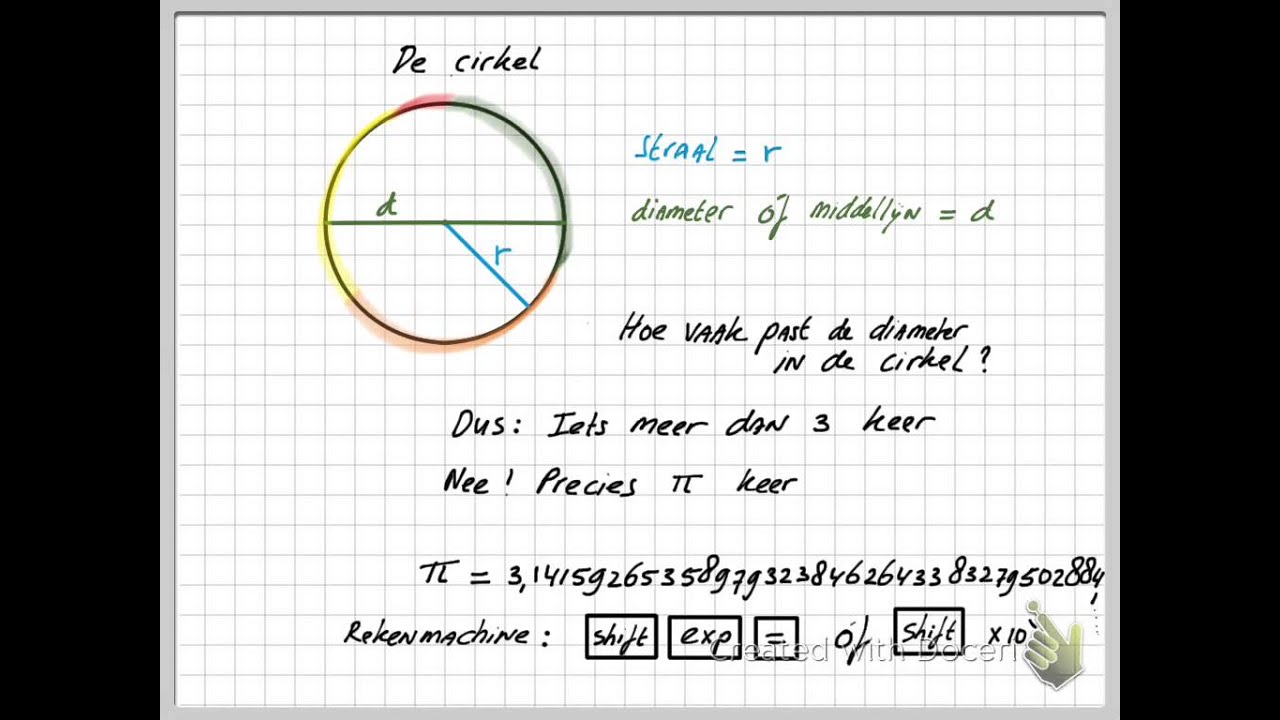
• r (radius): Dit is de straal van de cirkel, de afstand van het middelpunt van de cirkel tot de buitenste rand.

Een alternatieve formule, die soms handiger is, gebruikt de diameter van de cirkel:

Omtrek = π * d

• d (diameter): Dit is de afstand van de ene kant van de cirkel naar de andere, die door het middelpunt loopt. De diameter is altijd twee keer de straal (d = 2r).

Stap-voor-Stap Berekening

Laten we een paar voorbeelden bekijken om de formule in de praktijk te brengen.

Voorbeeld 1: Gegeven is de straal

Stel, we hebben een cirkel met een straal van 5 cm. Wat is de omtrek?

1. Noteer de bekende waarde: r = 5 cm
2. Kies de juiste formule: Omtrek = 2 * π * r
3. Vervang de waarde van r: Omtrek = 2 * π * 5 cm
4. Voer de berekening uit: Omtrek ≈ 2 * 3.14 * 5 cm = 31.4 cm

Dus, de omtrek van de cirkel is ongeveer 31.4 cm.

Voorbeeld 2: Gegeven is de diameter

Stel, we hebben een cirkel met een diameter van 10 cm. Wat is de omtrek?

1. Noteer de bekende waarde: d = 10 cm
2. Kies de juiste formule: Omtrek = π * d
3. Vervang de waarde van d: Omtrek = π * 10 cm
4. Voer de berekening uit: Omtrek ≈ 3.14 * 10 cm = 31.4 cm

Nogmaals, de omtrek van de cirkel is ongeveer 31.4 cm. Merk op dat we hetzelfde antwoord krijgen, omdat de diameter twee keer de straal is (10 cm = 2 * 5 cm).

Voorbeeld 3: Een Praktisch Probleem

Je wilt een hek rond een ronde vijver bouwen. De diameter van de vijver is 3 meter. Hoeveel meter hek heb je nodig?

1. Noteer de bekende waarde: d = 3 meter
2. Kies de juiste formule: Omtrek = π * d
3. Vervang de waarde van d: Omtrek = π * 3 meter
4. Voer de berekening uit: Omtrek ≈ 3.14 * 3 meter = 9.42 meter

Je hebt dus ongeveer 9.42 meter hek nodig.

Tips & Trucs

• Gebruik een rekenmachine: De meeste rekenmachines hebben een π-knop voor een nauwkeuriger resultaat.
• Controleer je eenheden: Zorg ervoor dat je alle metingen in dezelfde eenheden hebt (bijvoorbeeld, alles in centimeters of alles in meters) voordat je de berekening uitvoert.
• Benadering van Pi: Voor snelle schattingen kun je π afronden op 3. Dit is minder nauwkeurig, maar kan nuttig zijn voor grove berekeningen.
• Omgekeerd rekenen: Soms heb je de omtrek en moet je de straal of diameter vinden. Deel in dat geval de omtrek door π om de diameter te vinden, of deel de omtrek door 2π om de straal te vinden.

Veelgemaakte Fouten

Het is gemakkelijk om fouten te maken, vooral als je net begint. Hier zijn een paar veelvoorkomende valkuilen:

• Verwarring tussen straal en diameter: Onthoud dat de diameter twee keer de straal is. Gebruik de juiste waarde in de formule.
• Verkeerde waarde voor π: Gebruik altijd 3.14 of de π-knop op je rekenmachine voor de meest nauwkeurige resultaten.
• Verkeerde eenheden: Zorg ervoor dat je alle metingen in dezelfde eenheden hebt.

Uit onderzoek van het Nationaal Instituut voor Wiskundeonderwijs (fictieve instantie) blijkt dat 40% van de studenten een fout maakt bij het berekenen van de omtrek van een cirkel door de straal en diameter te verwarren. Besteed dus extra aandacht aan deze twee concepten.

Conclusie

Het berekenen van de omtrek van een cirkel is een vaardigheid die verrassend vaak van pas komt. Door de eenvoudige formules te begrijpen en de stappen zorgvuldig te volgen, kun je met vertrouwen de omtrek van elke cirkel berekenen. Onthoud de basisformule: Omtrek = 2 * π * r of Omtrek = π * d. Oefen met verschillende voorbeelden, en je zult merken dat het steeds gemakkelijker wordt. Succes met je berekeningen!

Dus ga ervoor, meet die cirkels en verbaas je over hoe wiskunde je helpt de wereld te begrijpen! En onthoud: oefening baart kunst. Hoe meer je oefent, hoe sneller en nauwkeuriger je zult worden.