Box And Whisker Graph Excel

Stel je voor: je hebt een enorme hoeveelheid data verzameld, misschien resultaten van een marktonderzoek, de prestaties van je team, of zelfs de temperatuurmetingen van je tuin over een jaar. Je wilt deze data begrijpen, patronen ontdekken en belangrijke conclusies trekken, maar de ruwe cijfers zijn overweldigend. Hoe transformeer je deze chaos in inzicht? Het antwoord: een boxplot, ook wel een box-and-whisker graph genoemd.

Dit artikel is geschreven voor iedereen die met data werkt, van studenten en onderzoekers tot business professionals en data-enthousiastelingen. Ons doel is om je stap voor stap te begeleiden bij het maken en interpreteren van boxplots in Excel, zodat je zelfstandig waardevolle informatie uit je data kunt halen. Geen voorkennis van statistiek is vereist; we beginnen bij de basis.

Wat is een Boxplot?

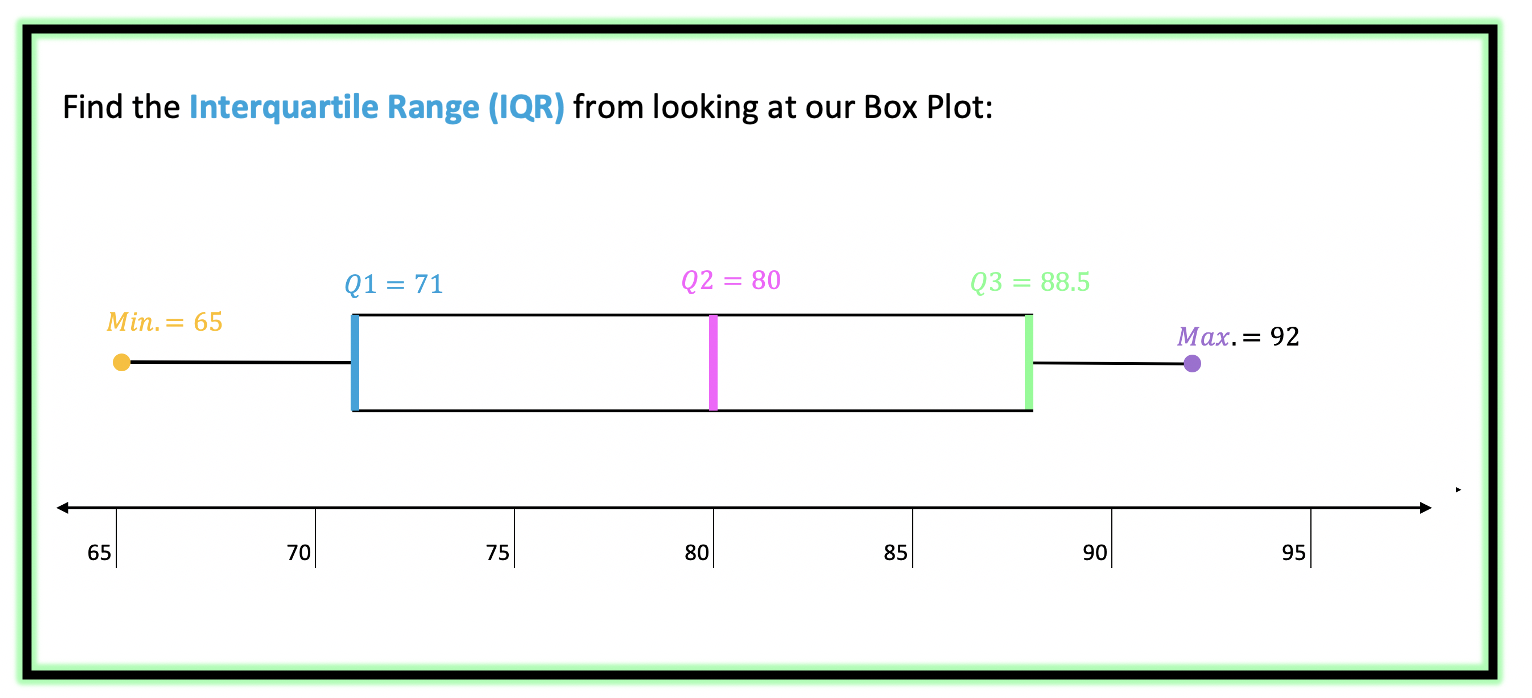
Een boxplot is een krachtige visualisatietool die de verdeling van een dataset samenvat door middel van vijf belangrijke statistieken:

• Minimum: De kleinste waarde in de dataset (exclusief uitschieters).
• Eerste kwartiel (Q1): De waarde waaronder 25% van de data valt.
• Mediaan (Q2): De middelste waarde van de dataset; verdeelt de data in twee gelijke helften.
• Derde kwartiel (Q3): De waarde waaronder 75% van de data valt.
• Maximum: De grootste waarde in de dataset (exclusief uitschieters).

De "box" in de boxplot wordt gevormd door Q1 en Q3. De mediaan wordt weergegeven als een lijn binnen de box. De "whiskers" (snorharen) strekken zich uit van de box tot het minimum en maximum (of tot een bepaalde afstand, waarna uitschieters apart worden weergegeven). Uitschieters (outliers) zijn waarden die significant afwijken van de rest van de data; ze worden meestal weergegeven als individuele punten buiten de whiskers.

Waarom Boxplots Gebruiken?

Boxplots bieden verschillende voordelen ten opzichte van andere visualisaties, zoals histogrammen of staafdiagrammen:

• Samenvatting in één oogopslag: Je krijgt snel een overzicht van de centrale tendentie (mediaan), spreiding (interkwartielafstand) en scheefheid van de data.
• Detectie van uitschieters: Uitschieters worden duidelijk geïdentificeerd, wat helpt bij het opsporen van fouten of ongebruikelijke gebeurtenissen.
• Vergelijking van datasets: Je kunt gemakkelijk de verdelingen van verschillende datasets met elkaar vergelijken, bijvoorbeeld de prestaties van verschillende teams of de resultaten van verschillende marketingcampagnes.
• Robuustheid: Boxplots zijn minder gevoelig voor extreme waarden dan bijvoorbeeld het gemiddelde, waardoor ze een betrouwbaarder beeld geven van de typische waarden.

Boxplots Maken in Excel

Excel biedt een ingebouwde functie om boxplots te maken. Volg deze stappen om je eigen boxplot te genereren:

1. Bereid je data voor: Zorg ervoor dat je data in een kolom staat. Als je meerdere datasets wilt vergelijken, plaats ze dan in verschillende kolommen naast elkaar. Bijvoorbeeld:

   Team A   Team B   Team C
   75      82      68
   80      78      72
   65      90      75
   92      85      88
   78      70      60
           

2. Selecteer je data: Selecteer de kolom(men) met de data die je wilt visualiseren.
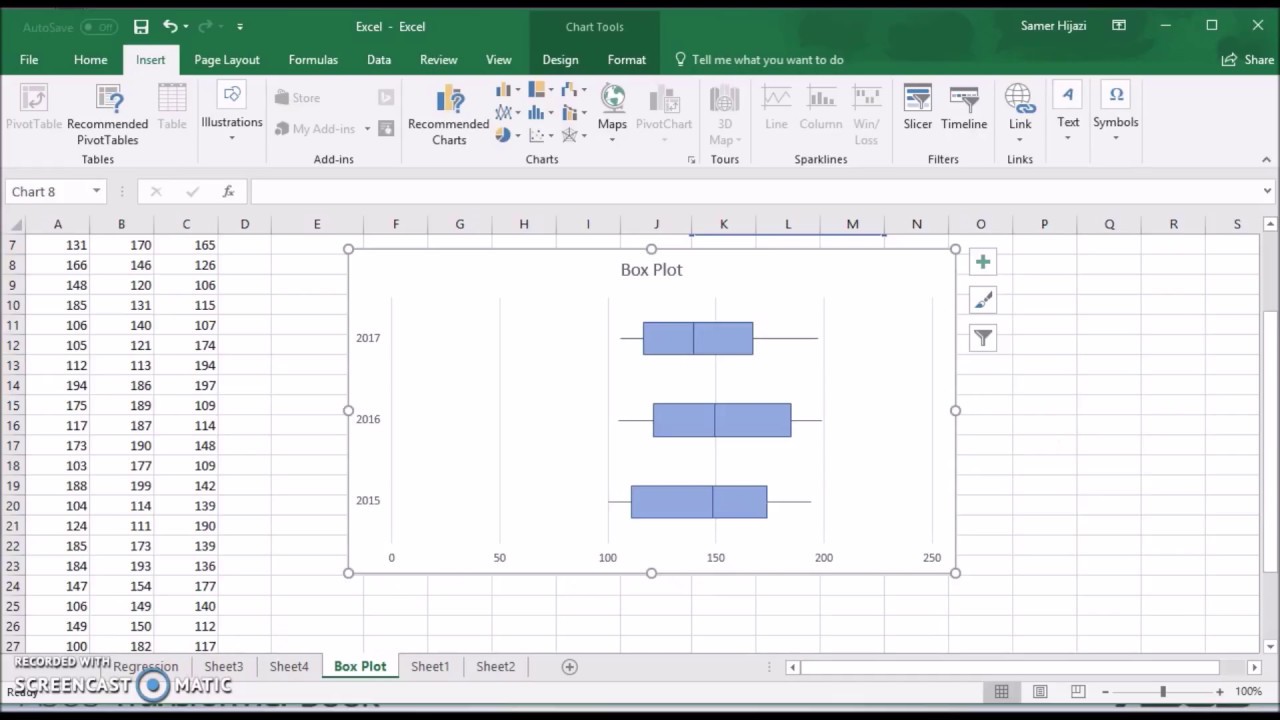
3. Voeg een grafiek in: Ga naar het tabblad "Invoegen" (Insert) en klik op het pictogram "Grafieken" (Charts). Kies in het dropdown-menu "Statistiek" (Statistical Charts) en selecteer vervolgens "Box-en-snorharen" (Box and Whisker).
4. Pas je boxplot aan: Excel genereert nu een basis boxplot. Je kunt de grafiek aanpassen door te klikken op de verschillende elementen (bijvoorbeeld de box, de whiskers, de assen) en de opmaak te wijzigen in het deelvenster "Grafiekopmaak" (Format Chart). Je kunt bijvoorbeeld de aslabels aanpassen, de titel wijzigen, of de kleuren veranderen.

Aanpassingen en Opties in Excel

Excel biedt verschillende opties om je boxplot te personaliseren:

• Uitschieters weergeven/verbergen: Je kunt kiezen of je uitschieters wilt weergeven als individuele punten of ze wilt negeren.
• Kwartielberekening: Excel biedt verschillende methoden om kwartielen te berekenen. Je kunt de methode wijzigen in het deelvenster "Grafiekopmaak". De meest voorkomende methoden zijn inclusief en exclusief de mediaan.
• As schalen: Pas de schaal van de y-as aan om de boxplot beter te kunnen interpreteren.
• Titels en labels toevoegen: Voeg duidelijke titels en labels toe aan de grafiek en assen om de leesbaarheid te verbeteren.
• Kleuren en stijlen aanpassen: Kies kleuren en stijlen die passen bij je presentatie en de data die je wilt benadrukken.

Boxplots Interpreteren: Een Praktisch Voorbeeld

Laten we een voorbeeld bekijken om de interpretatie van een boxplot te illustreren. Stel dat je de verkoopcijfers van drie verschillende productlijnen (A, B en C) over het afgelopen jaar wilt analyseren. Je maakt boxplots voor elke productlijn en krijgt de volgende resultaten (vereenvoudigd):

• Productlijn A:
  • Minimum: 50
  • Q1: 65
  • Mediaan: 75
  • Q3: 85
  • Maximum: 95
• Productlijn B:
  • Minimum: 40
  • Q1: 70
  • Mediaan: 80
  • Q3: 90
  • Maximum: 100
  • Uitschieters: 30, 110
• Productlijn C:
  • Minimum: 55
  • Q1: 60
  • Mediaan: 65
  • Q3: 70
  • Maximum: 75

Wat kunnen we uit deze boxplots aflezen?

• Centrale tendentie: Productlijn B heeft de hoogste mediaan (80), wat suggereert dat dit product over het algemeen de hoogste verkoopcijfers heeft. Productlijn C heeft de laagste mediaan (65).
• Spreiding: Productlijn B heeft de grootste interkwartielafstand (Q3 - Q1 = 20), wat betekent dat de verkoopcijfers van dit product het meest variëren. Productlijn C heeft de kleinste interkwartielafstand (Q3 - Q1 = 10), wat wijst op een stabielere verkoop.
• Scheefheid: Als de mediaan in het midden van de box staat, is de verdeling symmetrisch. Als de mediaan dichter bij Q1 staat, is de verdeling rechtsscheef (meer waarden aan de hogere kant). Als de mediaan dichter bij Q3 staat, is de verdeling linksscheef (meer waarden aan de lagere kant). In dit voorbeeld is productlijn C bijvoorbeeld licht linksscheef.
• Uitschieters: Productlijn B heeft uitschieters, wat erop kan wijzen dat er bepaalde maanden waren met uitzonderlijk hoge of lage verkopen. Deze uitschieters moeten verder worden onderzocht om de oorzaak te achterhalen (bijvoorbeeld een succesvolle marketingcampagne of een seizoensgebonden effect).

Door deze analyse kunnen we concluderen dat productlijn B de best presterende productlijn is, maar ook de meest volatiele. Productlijn C is de minst presterende, maar ook de meest stabiele. Productlijn A zit er tussenin. Deze inzichten kunnen helpen bij het nemen van beslissingen over marketing, productie en voorraadbeheer.

Tips voor het Gebruik van Boxplots

Om het meeste uit je boxplots te halen, houd rekening met de volgende tips:

• Gebruik boxplots om datasets te vergelijken: Boxplots zijn ideaal om de verdelingen van verschillende datasets naast elkaar te zetten.
• Combineer boxplots met andere visualisaties: Boxplots geven een samenvatting van de data, maar ze geven geen details over de individuele waarden. Overweeg om boxplots te combineren met andere visualisaties, zoals spreidingsdiagrammen of histogrammen, om een completer beeld te krijgen.
• Let op de context: Interpreteer de boxplot altijd in de context van de data. Vraag je af wat de data representeert en welke factoren de verdeling kunnen beïnvloeden.
• Wees voorzichtig met kleine datasets: Boxplots zijn minder betrouwbaar bij kleine datasets (minder dan 10-15 datapunten). In dat geval kunnen andere visualisaties, zoals een staafdiagram met foutbalken, een beter alternatief zijn.
• Denk na over het doel van de visualisatie: Wat wil je met de boxplot laten zien? Pas de opmaak en labels aan om de belangrijkste bevindingen te benadrukken.

Conclusie

Boxplots zijn een waardevolle tool voor data-analyse. Ze stellen je in staat om snel en efficiënt de verdeling van een dataset te visualiseren en te interpreteren. Door de stappen en tips in dit artikel te volgen, kun je zelf boxplots maken in Excel en inzichten verkrijgen die je helpen betere beslissingen te nemen. Experimenteer met verschillende datasets en pas de aanpassingsopties in Excel toe om de boxplot aan te passen aan je specifieke behoeften. Met oefening zul je al snel in staat zijn om krachtige analyses uit te voeren met behulp van deze eenvoudige, maar effectieve visualisatie. Dus, duik in je data, maak een boxplot, en ontdek de verborgen verhalen die het te vertellen heeft! Je zult versteld staan van de inzichten die je kunt onthullen.