Breuken Procenten Kommagetallen En Verhoudingen Samenvatting
Heb je ooit het gevoel gehad dat je verdwaalt in een doolhof van cijfers en symbolen? Breuken, procenten, kommagetallen en verhoudingen: ze lijken op het eerste gezicht misschien ingewikkeld, maar ze zijn essentieel in ons dagelijks leven. Van het berekenen van kortingen in de winkel tot het begrijpen van recepten en het analyseren van statistieken, deze wiskundige concepten komen overal terug. Deze samenvatting is bedoeld voor iedereen die zijn basiskennis wil opfrissen, wiskunde studenten die een beknopt overzicht zoeken of simpelweg nieuwsgierig zijn naar de wondere wereld van de getallen. Samen gaan we deze concepten ontrafelen en laten zien hoe ze met elkaar verbonden zijn.
De Basis: Breuken
Een breuk vertegenwoordigt een deel van een geheel. Het bestaat uit twee delen:
- De teller: Het aantal delen dat we hebben.
- De noemer: Het totale aantal gelijke delen waaruit het geheel bestaat.
Bijvoorbeeld, de breuk 3/4 betekent dat we 3 delen hebben van een geheel dat in 4 gelijke delen is verdeeld. Denk aan een pizza die in 4 stukken is gesneden, en jij eet er 3 van. Dan heb je 3/4 van de pizza opgegeten.
Verschillende soorten breuken
- Echte breuk: De teller is kleiner dan de noemer (bijv. 1/2, 2/3, 7/8). Deze breuken zijn kleiner dan 1.
- Onechte breuk: De teller is groter dan of gelijk aan de noemer (bijv. 5/4, 8/8, 11/3). Deze breuken zijn groter dan of gelijk aan 1.
- Gemengde breuk: Bestaat uit een geheel getal en een echte breuk (bijv. 1 1/2, 2 3/4). Dit is een andere manier om een onechte breuk weer te geven.
Rekenen met breuken
Breuken optellen en aftrekken vereist dat ze dezelfde noemer hebben. Als de noemers verschillend zijn, moeten we ze eerst gelijk maken. Dit doen we door de breuken te vermenigvuldigen met een factor die ervoor zorgt dat ze dezelfde noemer krijgen. Bijvoorbeeld:
1/2 + 1/4 = ?
We vermenigvuldigen 1/2 met 2/2 (wat gelijk is aan 1, dus de waarde van de breuk verandert niet):
(1/2) * (2/2) = 2/4
Nu kunnen we optellen:
2/4 + 1/4 = 3/4
Breuken vermenigvuldigen is eenvoudiger: we vermenigvuldigen de tellers met elkaar en de noemers met elkaar.
1/2 * 1/3 = (1 * 1) / (2 * 3) = 1/6
Breuken delen is hetzelfde als vermenigvuldigen met het omgekeerde van de tweede breuk. Het omgekeerde van een breuk is de breuk waar teller en noemer zijn omgedraaid.
1/2 : 1/3 = 1/2 * 3/1 = 3/2
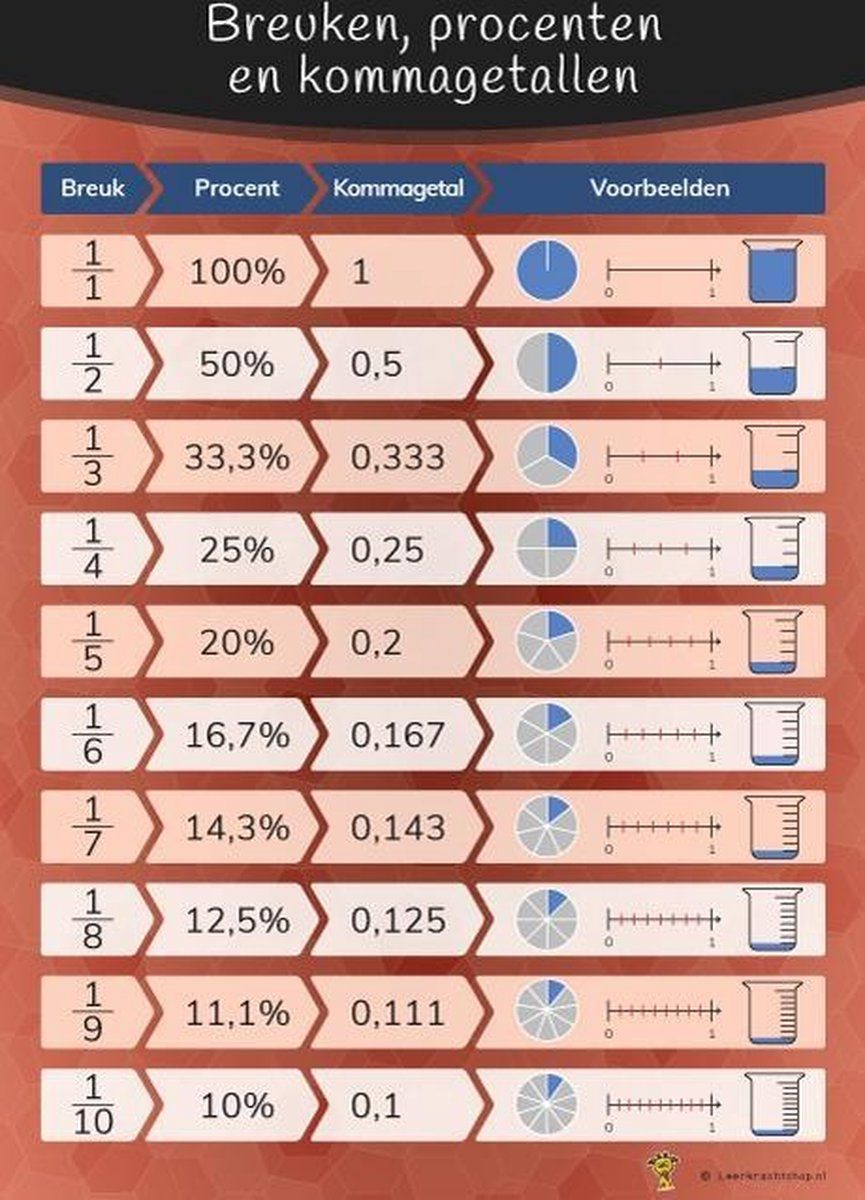
Van Breuken naar Procenten
Een procent is eigenlijk gewoon een breuk met 100 als noemer. Het woord "procent" betekent letterlijk "per honderd". Een percentage geeft dus aan hoeveel delen er zijn van de 100. Het symbool voor procent is %.
Om een breuk om te zetten naar een percentage, vermenigvuldigen we de breuk met 100%. Bijvoorbeeld:
1/2 = (1/2) * 100% = 50%
3/4 = (3/4) * 100% = 75%
Omgekeerd, om een percentage om te zetten naar een breuk, delen we het percentage door 100 en vereenvoudigen we de breuk indien mogelijk. Bijvoorbeeld:
25% = 25/100 = 1/4
80% = 80/100 = 4/5
Procenten worden gebruikt om veranderingen, kortingen en winstmarges aan te geven. Stel je voor: je favoriete winkel biedt 20% korting op een trui van €50. Om de korting te berekenen, vermenigvuldig je 20% (of 0.20) met €50: 0.20 * €50 = €10 korting. De trui kost nu €50 - €10 = €40.
Kommagetallen: Een Andere Weergave
Een kommagetal is een andere manier om een breuk weer te geven. Het gebruikt een punt (of komma, afhankelijk van de conventie) om het gehele getal te scheiden van het fractionele deel. Elke positie rechts van de komma vertegenwoordigt een macht van 10 in de noemer: tienden, honderdsten, duizendsten, enzovoort.
Om een breuk om te zetten naar een kommagetal, delen we de teller door de noemer. Bijvoorbeeld:
1/4 = 1 : 4 = 0.25
3/8 = 3 : 8 = 0.375
Omgekeerd, om een kommagetal om te zetten naar een breuk, schrijven we het kommagetal als een breuk met een macht van 10 in de noemer en vereenvoudigen we de breuk. Bijvoorbeeld:
0.75 = 75/100 = 3/4
0.125 = 125/1000 = 1/8
Rekenen met kommagetallen is vergelijkbaar met rekenen met gehele getallen, maar we moeten rekening houden met de positie van de komma. Bij het optellen en aftrekken zorgen we ervoor dat de komma's onder elkaar staan, zodat we de juiste posities optellen of aftrekken.
Verhoudingen: Relaties tussen Hoeveelheden
Een verhouding vergelijkt twee of meer hoeveelheden. Het geeft aan hoe de hoeveelheden zich tot elkaar verhouden. We kunnen een verhouding schrijven als a:b, waarbij a en b de hoeveelheden zijn die we vergelijken.
Bijvoorbeeld, als er 12 jongens en 18 meisjes in een klas zitten, dan is de verhouding van jongens tot meisjes 12:18. We kunnen deze verhouding vereenvoudigen door beide getallen te delen door hun grootste gemene deler (in dit geval 6):
12:18 = (12/6):(18/6) = 2:3
Dit betekent dat er voor elke 2 jongens, 3 meisjes zijn in de klas.
Verhoudingen worden gebruikt in recepten, schaalmodellen, en het verdelen van taken. Stel je voor dat een recept voor een cake de verhouding bloem tot suiker aangeeft als 3:2. Als je een grotere cake wilt maken en 6 koppen bloem gebruikt, hoeveel koppen suiker heb je dan nodig?
We kunnen een proportie gebruiken om dit op te lossen:
3/2 = 6/x
Om x te vinden, kruiselings vermenigvuldigen we:
3x = 12
x = 4
Dus je hebt 4 koppen suiker nodig.
De Onderlinge Verbanden
Het is cruciaal te beseffen dat breuken, procenten, kommagetallen en verhoudingen niet los van elkaar staan. Ze zijn verschillende manieren om dezelfde hoeveelheid of relatie weer te geven. Het beheersen van de vaardigheid om tussen deze vormen te schakelen, geeft je een krachtig hulpmiddel om problemen op te lossen en de wereld om je heen beter te begrijpen.
Hier is een tabel die de onderlinge relaties samenvat:
| Breuk | Procent | Kommagetal |
|---|---|---|
| 1/2 | 50% | 0.5 |
| 1/4 | 25% | 0.25 |
| 3/4 | 75% | 0.75 |
| 1/5 | 20% | 0.2 |
Oefening baart kunst! Hoe meer je oefent met het omzetten tussen deze vormen en het toepassen ervan in praktische situaties, hoe comfortabeler je ermee zult worden. Denk aan het berekenen van fooien in een restaurant, het vergelijken van prijzen in de supermarkt, of het begrijpen van de statistieken in het nieuws. Elke keer dat je deze concepten gebruikt, versterk je je begrip en bouw je aan een stevige wiskundige basis.
We hopen dat deze samenvatting je geholpen heeft om breuken, procenten, kommagetallen en verhoudingen beter te begrijpen. Blijf oefenen en blijf nieuwsgierig! Wiskunde is geen obstakel, maar een krachtige tool die je helpt om de wereld om je heen te begrijpen en te navigeren. Nu je deze basisprincipes beheerst, ben je klaar om complexere wiskundige uitdagingen aan te gaan. Succes!
Bekijk ook deze gerelateerde berichten:
- Welk Stripfiguur Begroet Iedereen Met Hoi Pipeloi
- Duitse Uitvinder Van Een Motor Zonder Cilinders En Zuigers
- Hoelang Duurt Een Bevalling Gemiddeld
- Van Fahrenheit Naar Celsius Omrekenen
- De Rank Waddinxveen Kerkdiensten
- Hoeveel Woorden Heeft De Engelse Taal
- Is Engeland Lid Van De Eu
- Chinese Cultuur Normen En Waarden
- Romeinse Godin Van Het Huwelijk
- Lord Of The Rings Acteur Overleden
