Chi Square And P Value
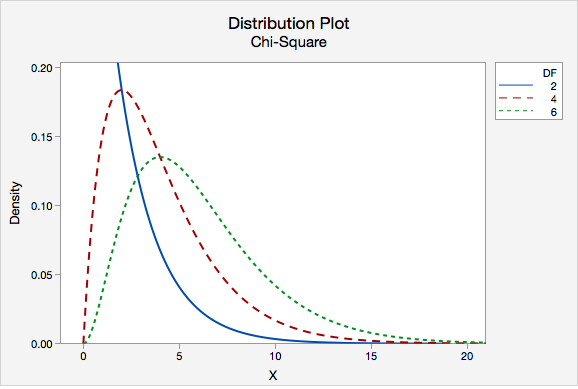
Het begrijpen van statistiek kan soms voelen alsof je een doolhof betreedt zonder kaart. Veel mensen, zelfs professionals, vinden termen als Chi-kwadraat en p-waarde intimiderend. Dit is begrijpelijk! Statistiek is niet altijd intuïtief. Maar het goede nieuws is dat je deze concepten kunt begrijpen zonder een wiskundig genie te zijn. In dit artikel zullen we deze concepten ontrafelen, de toepassing ervan in de echte wereld laten zien, en je helpen de relevantie ervan in te zien.
Wat is Chi-kwadraat?
Stel je voor: je bent een onderzoeker en je wilt weten of er een verband is tussen twee categorische variabelen. Categorische variabelen zijn variabelen die in groepen of categorieën kunnen worden ingedeeld, zoals geslacht (man/vrouw), opleidingsniveau (basisschool, middelbare school, hoger onderwijs) of politieke voorkeur (links, rechts, midden). De Chi-kwadraat toets is een statistische tool die je helpt om precies dat te doen. Het helpt je te bepalen of er een significant verschil is tussen de verwachte frequentie en de waargenomen frequentie in een of meer categorieën.
Laten we dit verduidelijken met een voorbeeld. Stel dat je wilt onderzoeken of er een verband is tussen het roken van sigaretten en het krijgen van longkanker. Je verzamelt gegevens van een groep mensen en deelt ze in twee categorieën in: rokers en niet-rokers, en mensen met longkanker en mensen zonder longkanker. De Chi-kwadraat toets zal je helpen te bepalen of de verdeling van longkanker over deze twee groepen (rokers en niet-rokers) statistisch significant verschilt van wat je zou verwachten als er geen verband zou zijn tussen roken en longkanker.
Hoe werkt de Chi-kwadraat toets?
De Chi-kwadraat toets berekent een Chi-kwadraat statistiek. Deze statistiek meet de afwijking tussen de verwachte en waargenomen frequenties. Een hogere Chi-kwadraat waarde duidt op een grotere afwijking, wat suggereert dat er mogelijk een verband is tussen de variabelen.
De formule voor de Chi-kwadraat statistiek is:
χ² = Σ [(O - E)² / E]
Waar:
- χ² = Chi-kwadraat statistiek
- Σ = Sommatie (optelling)
- O = Waargenomen frequentie
- E = Verwachte frequentie
De formule ziet er misschien eng uit, maar het idee is eenvoudig: voor elke cel in je tabel bereken je het verschil tussen wat je observeert en wat je verwacht, kwadrateer je dat verschil, deel je dat door de verwachte waarde, en tel je al die resultaten op. Hoe groter de verschillen, hoe groter de Chi-kwadraat waarde.
Voorbeeld:
Stel dat we een onderzoek doen naar de relatie tussen automerk (A, B, C) en kleur (rood, blauw, groen). We verzamelen data en krijgen de volgende waarnemingen:
| Rood | Blauw | Groen | Totaal | |
|---|---|---|---|---|
| Merk A | 20 | 15 | 10 | 45 |
| Merk B | 10 | 25 | 15 | 50 |
| Merk C | 5 | 10 | 20 | 35 |
| Totaal | 35 | 50 | 45 | 130 |
De Chi-kwadraat toets zal ons helpen te bepalen of de verdeling van kleuren verschilt afhankelijk van het automerk.
De P-waarde: De sleutel tot significantie
De p-waarde is een cruciale component in de interpretatie van de Chi-kwadraat toets (en vele andere statistische toetsen). Het is de kans dat je de waargenomen resultaten (of resultaten die nog extremer zijn) zou krijgen, *als er in werkelijkheid geen verband is* tussen de variabelen die je onderzoekt. Met andere woorden, het is de kans dat je resultaten puur toeval zijn.
Voorbeeld:
Stel, na het uitvoeren van de Chi-kwadraat toets op de data over roken en longkanker, vinden we een p-waarde van 0.03. Dit betekent dat er een kans van 3% is dat we de waargenomen associatie tussen roken en longkanker zouden zien, *als er in werkelijkheid geen verband is*. Met andere woorden, als roken geen invloed zou hebben op het krijgen van longkanker, dan is er 3% kans dat we toch deze resultaten zouden zien.
Significantieniveau (α)
Om te bepalen of een p-waarde significant is, vergelijken we deze met een vooraf bepaald significantieniveau, aangeduid met de Griekse letter alfa (α). Het meest gebruikelijke significantieniveau is 0.05 (5%).
Beslissingsregels:
- Als de p-waarde kleiner is dan of gelijk aan het significantieniveau (p ≤ α), dan verwerpen we de nulhypothese. Dit betekent dat we concluderen dat er een statistisch significant verband is tussen de variabelen.
- Als de p-waarde groter is dan het significantieniveau (p > α), dan verwerpen we de nulhypothese niet. Dit betekent dat we geen bewijs hebben om te concluderen dat er een statistisch significant verband is tussen de variabelen.
In het voorbeeld van roken en longkanker, met een p-waarde van 0.03 en een significantieniveau van 0.05, zouden we de nulhypothese verwerpen. We zouden concluderen dat er een statistisch significant verband is tussen roken en longkanker.
Wat is de nulhypothese?
De nulhypothese is een statement dat er geen verband is tussen de variabelen die je onderzoekt. In het voorbeeld van roken en longkanker zou de nulhypothese zijn: "Er is geen verband tussen roken en het krijgen van longkanker." We proberen deze nulhypothese te verwerpen met onze statistische toetsen.
Het belang in de echte wereld
De Chi-kwadraat toets en de p-waarde zijn krachtige tools die in verschillende disciplines worden gebruikt:
- Medisch onderzoek: Beoordelen of een nieuwe behandeling effectief is, de relatie tussen levensstijlfactoren en ziekten onderzoeken.
- Marketing: Onderzoeken of er een verband is tussen reclamecampagnes en verkoopcijfers, klantvoorkeuren analyseren.
- Politieke wetenschappen: Analyse van de relatie tussen demografische gegevens en stemgedrag, meningen peilen.
- Sociologie: Onderzoek naar de relatie tussen sociaaleconomische status en toegang tot onderwijs, de impact van sociale programma's evalueren.
Denk bijvoorbeeld aan een farmaceutisch bedrijf dat een nieuw medicijn test. De Chi-kwadraat toets kan worden gebruikt om te analyseren of er een significant verschil is in het genezingspercentage tussen de groep die het medicijn krijgt en de placebogroep. De p-waarde helpt dan te bepalen of dit verschil te wijten is aan het medicijn of aan toeval.
Kritiek en kanttekeningen
Hoewel de Chi-kwadraat toets een nuttig instrument is, is het belangrijk om de beperkingen ervan te begrijpen:
- Gevoelig voor steekproefomvang: Met een voldoende grote steekproef kan bijna elk verband statistisch significant worden, zelfs als het in de praktijk weinig relevant is.
- Alleen geschikt voor categorische data: De Chi-kwadraat toets kan niet worden gebruikt voor continue variabelen (bijv. leeftijd, gewicht).
- Geeft geen informatie over de sterkte van het verband: De Chi-kwadraat toets vertelt je alleen *of* er een verband is, niet *hoe sterk* dat verband is. Voor de sterkte van het verband zijn andere statistische maatstaven nodig.
- Aanname van onafhankelijkheid: De waarnemingen moeten onafhankelijk van elkaar zijn. Als de waarnemingen afhankelijk zijn, kan de Chi-kwadraat toets onjuiste resultaten opleveren.
Sommige statistici betogen dat de focus op p-waarden kan leiden tot overhaaste conclusies en het negeren van andere belangrijke factoren, zoals de grootte van het effect en de relevantie in de praktijk. Het is belangrijk om statistische significantie niet te verwarren met praktische significantie. Een statistisch significant resultaat is niet per definitie belangrijk of nuttig in de echte wereld.
Conclusie: Een fundament voor kritisch denken
De Chi-kwadraat toets en de p-waarde zijn waardevolle tools voor het analyseren van categorische data en het trekken van conclusies over mogelijke verbanden tussen variabelen. Echter, het is cruciaal om deze tools met voorzichtigheid en kritisch denken te gebruiken. Begrijp de beperkingen, interpreteer de resultaten in de context van de onderzoeksvraag en de steekproef, en overweeg andere factoren die de resultaten kunnen beïnvloeden.
Door een beter begrip van deze statistische concepten kun je kritischer kijken naar informatie en onderzoeksresultaten die je tegenkomt, of het nu in de media, in wetenschappelijke publicaties of in je eigen werk is. Je bent beter in staat om beweringen te evalueren, te beoordelen of conclusies gerechtvaardigd zijn, en je eigen beslissingen te nemen op basis van evidence.
Nu je de basisprincipes van de Chi-kwadraat toets en de p-waarde begrijpt, waar zou je deze kennis in jouw vakgebied of interessegebied kunnen toepassen? Wat zou je willen onderzoeken of analyseren?


Bekijk ook deze gerelateerde berichten:
- En Ook Niet 4 Letters
- Wat Is Links En Rechts In De Politiek
- Is 12 Midday Am Or Pm
- Voordeel Zittende Minister President Verkiezingen
- Het Is Bedoeld Of Bedoelt
- Van Welke Staat Is Salt Lake City De Hoofdstad
- Present Perfect And Present Perfect Continuous Exercises
- Van Buik Naar Rug Draaien
- Leuke Proefjes Voor In De Klas
- Is Een Fietshelm Verplicht In Frankrijk
