Chi Square Goodness Of Fit

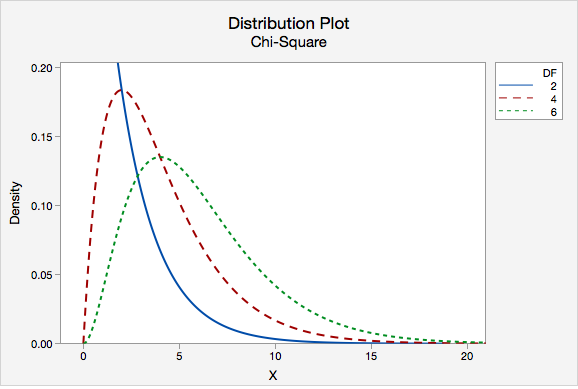
Laten we eerlijk zijn, statistiek kan soms aanvoelen als een doolhof. Zeker als je probeert te bepalen of de data die je verzameld hebt, eigenlijk wel overeenkomt met wat je verwacht te zien. Je bent niet de enige. Veel onderzoekers, marketeers en zelfs studenten worstelen hiermee. De Chi-kwadraat goodness-of-fit test is een krachtig hulpmiddel dat je kan helpen om deze worsteling te verminderen. In dit artikel duiken we in deze test, ontrafelen we de complexiteit en laten we zien hoe je hem in de praktijk kunt toepassen.

Wat is de Chi-kwadraat Goodness-of-Fit Test?

De Chi-kwadraat goodness-of-fit test (ook wel bekend als de Chi-kwadraat aanpassingstoets) is een statistische test die gebruikt wordt om te bepalen of een waargenomen frequentieverdeling significant verschilt van een verwachte frequentieverdeling. Met andere woorden, het helpt je te bepalen of je data "goed past" bij een bepaalde theoretische verdeling of hypothese. Denk hierbij aan situaties waarin je wilt nagaan of de verdeling van kleuren M&M's overeenkomt met wat Mars beweert, of dat de politieke voorkeur van een steekproef overeenkomt met de nationale verdeling.

Waarom is dit belangrijk? Stel je voor dat je een nieuwe marketingcampagne lanceert en je vermoedt dat deze een bepaalde impact zal hebben op de merkbekendheid. De Chi-kwadraat goodness-of-fit test kan je helpen te bepalen of de resultaten van je campagne daadwerkelijk significant afwijken van wat je zou verwachten zonder de campagne. Dit is cruciaal voor het nemen van geïnformeerde beslissingen.

De Formule ontrafeld

De formule voor de Chi-kwadraat goodness-of-fit test ziet er als volgt uit:

χ² = Σ [(O_i - E_i)² / E_i]

Waar:

• χ² de Chi-kwadraat test statistiek is.
• Σ staat voor de sommatie (optelling).
• O_i staat voor de waargenomen frequentie voor categorie i.
• E_i staat voor de verwachte frequentie voor categorie i.

Simpel gezegd: Voor elke categorie bereken je het verschil tussen de waargenomen en de verwachte waarde, kwadrateer je dat verschil, deel je het door de verwachte waarde, en tel je al die resultaten bij elkaar op. Dat geeft je de Chi-kwadraat waarde.

Wanneer Gebruik je de Chi-kwadraat Goodness-of-Fit Test?

De Chi-kwadraat goodness-of-fit test is geschikt voor situaties waarin:

• Je categorische data hebt. (Data die in categorieën verdeeld kan worden, zoals kleuren, politieke voorkeuren, etc.)
• Je wilt nagaan of de waargenomen frequenties overeenkomen met een verwachte frequentieverdeling.
• Je een onafhankelijke variabele hebt met verschillende categorieën.
• Je voldoende grote steekproef hebt (dit is belangrijk voor de betrouwbaarheid van de test). Vuistregel is dat alle verwachte frequenties groter dan 5 moeten zijn.

Voorbeelden:

• Genetica: Nagaan of de verdeling van genotypen in een populatie overeenkomt met de verwachte verdeling volgens de wetten van Mendel.
• Marketing: Controleren of de voorkeur voor verschillende merken in een steekproef overeenkomt met de marktaandelen.
• Kwaliteitscontrole: Nagaan of het aantal defecte producten in een partij overeenkomt met een acceptabel foutpercentage.
• Sociale wetenschappen: Onderzoeken of de verdeling van opleidingsniveaus in een bepaalde regio overeenkomt met de nationale verdeling.

Stappen voor het uitvoeren van een Chi-kwadraat Goodness-of-Fit Test

1. Formuleer je hypothesen:
• Nulhypothese (H0): Er is geen significant verschil tussen de waargenomen en de verwachte frequentieverdeling.
• Alternatieve hypothese (H1): Er is wel een significant verschil tussen de waargenomen en de verwachte frequentieverdeling.
2. Verzamel je data: Tel het aantal waarnemingen in elke categorie.
3. Bereken de verwachte frequenties: Dit is afhankelijk van de hypothese die je test. Bijvoorbeeld, als je test of de verdeling uniform is, dan is de verwachte frequentie voor elke categorie gelijk aan het totale aantal waarnemingen gedeeld door het aantal categorieën.
4. Bereken de Chi-kwadraat test statistiek (χ²): Gebruik de formule zoals eerder besproken.
5. Bepaal de vrijheidsgraden (df): De vrijheidsgraden zijn gelijk aan het aantal categorieën minus 1 (df = aantal categorieën - 1).
6. Bepaal de kritieke waarde of de p-waarde: Gebruik een Chi-kwadraat tabel of een statistisch softwarepakket om de kritieke waarde of de p-waarde te bepalen, gebaseerd op de vrijheidsgraden en het significantieniveau (α). Het significantieniveau is meestal 0.05.
7. Neem een beslissing:
• Als de Chi-kwadraat test statistiek groter is dan de kritieke waarde, of als de p-waarde kleiner is dan het significantieniveau (α), verwerp dan de nulhypothese. Dit betekent dat er een significant verschil is tussen de waargenomen en de verwachte frequentieverdeling.
• Als de Chi-kwadraat test statistiek kleiner is dan de kritieke waarde, of als de p-waarde groter is dan het significantieniveau (α), verwerp dan de nulhypothese niet. Dit betekent dat er geen significant verschil is tussen de waargenomen en de verwachte frequentieverdeling.
8. Conclusie: Interpreteer je resultaten in de context van je onderzoeksvraag.

Een Praktisch Voorbeeld: Kleuren M&M's

Stel, je wilt controleren of de verdeling van kleuren M&M's in een zak overeenkomt met de door Mars geclaimde verdeling. Mars beweert de volgende percentages:

• Bruin: 13%
• Geel: 14%
• Rood: 13%
• Blauw: 24%
• Oranje: 20%
• Groen: 16%

Je koopt een zak M&M's en telt de kleuren. Je vindt de volgende waargenomen frequenties:

• Bruin: 10
• Geel: 15
• Rood: 11
• Blauw: 28
• Oranje: 18
• Groen: 18
• Totaal: 100

Nu bereken je de verwachte frequenties, gebaseerd op de percentages van Mars. Bijvoorbeeld, de verwachte frequentie voor bruine M&M's is 13% van 100, dus 13.

• Bruin: 13
• Geel: 14
• Rood: 13
• Blauw: 24
• Oranje: 20
• Groen: 16

Vervolgens bereken je de Chi-kwadraat test statistiek:

χ² = [(10-13)²/13] + [(15-14)²/14] + [(11-13)²/13] + [(28-24)²/24] + [(18-20)²/20] + [(18-16)²/16] ≈ 2.56

De vrijheidsgraden zijn 6 (aantal kleuren) - 1 = 5.

Met een significantieniveau van 0.05 en 5 vrijheidsgraden, is de kritieke waarde van de Chi-kwadraat verdeling ongeveer 11.07.

Omdat de Chi-kwadraat test statistiek (2.56) kleiner is dan de kritieke waarde (11.07), verwerpen we de nulhypothese niet. Dit betekent dat er geen significant bewijs is om te concluderen dat de verdeling van kleuren M&M's in jouw zak significant verschilt van de door Mars geclaimde verdeling.

Aandachtspunten en Mogelijke Kritiek

Hoewel de Chi-kwadraat goodness-of-fit test een waardevol hulpmiddel is, is het belangrijk om te onthouden dat het niet perfect is. Enkele aandachtspunten en mogelijke kritiekpunten zijn:

• Steekproefgrootte: De test is gevoelig voor kleine steekproeven. Als de steekproefgrootte te klein is, kan de test onbetrouwbare resultaten opleveren. Zoals eerder vermeld, is het belangrijk dat alle verwachte frequenties groter zijn dan 5.
• Verwachte frequenties: De test werkt het beste als de verwachte frequenties redelijk gelijk verdeeld zijn. Als sommige verwachte frequenties erg laag zijn, kan dit de resultaten vertekenen.
• Alleen associatie, geen causaliteit: De test kan alleen aantonen of er een associatie is tussen de waargenomen en de verwachte verdeling, maar het kan geen causaliteit aantonen.
• Alternatieve methoden: Er zijn andere statistische testen die gebruikt kunnen worden om de goodness-of-fit te beoordelen, zoals de Kolmogorov-Smirnov test, die geschikter kan zijn voor continue data.

Sommige critici beweren dat de Chi-kwadraat test te vaak gebruikt wordt zonder voldoende aandacht te besteden aan de aannames. Het is belangrijk om de aannames van de test zorgvuldig te controleren voordat je de test uitvoert, en om de resultaten voorzichtig te interpreteren.

Oplossingen en Verbeteringen

Gelukkig zijn er manieren om de nadelen van de Chi-kwadraat goodness-of-fit test te verminderen:

• Verhoog de steekproefgrootte: Een grotere steekproefgrootte zal de betrouwbaarheid van de test verhogen.
• Combineer categorieën: Als sommige verwachte frequenties erg laag zijn, overweeg dan om categorieën samen te voegen. Dit kan echter leiden tot verlies van informatie.
• Gebruik een Yates' correctie: Voor 2x2 tabellen (twee categorieën voor beide variabelen) kan een Yates' correctie gebruikt worden om de Chi-kwadraat test statistiek aan te passen en de kans op een type I fout (een valse positieve) te verminderen.
• Overweeg alternatieve testen: Als de aannames van de Chi-kwadraat test niet voldaan zijn, overweeg dan om een alternatieve test te gebruiken, zoals de Kolmogorov-Smirnov test.

De Chi-kwadraat Goodness-of-Fit Test in de Toekomst

Met de toenemende beschikbaarheid van data en de groeiende behoefte aan data-gedreven beslissingen, zal de Chi-kwadraat goodness-of-fit test een belangrijke rol blijven spelen in verschillende vakgebieden. De test kan worden gebruikt om de effectiviteit van interventies te evalueren, trends te identificeren en voorspellingen te doen.

Denk bijvoorbeeld aan:

• Het voorspellen van verkiezingsuitslagen op basis van opiniepeilingen.
• Het monitoren van de verspreiding van ziekten.
• Het evalueren van de impact van overheidsbeleid.

De sleutel tot succes ligt in het correct toepassen en interpreteren van de test, rekening houdend met de aannames en de beperkingen.

Hopelijk heeft dit artikel de Chi-kwadraat goodness-of-fit test een stuk duidelijker gemaakt. Het is een krachtig instrument, maar zoals elk instrument, vereist het begrip en zorgvuldigheid. Nu, denk eens na: hoe zou jij de Chi-kwadraat goodness-of-fit test kunnen inzetten in jouw eigen werk of studie?