Diameter Cirkel Berekenen Met Oppervlakte

Heb je ooit een cirkel gezien en gedacht: "Hoe groot is die eigenlijk?" Of misschien heb je de oppervlakte van een cirkel berekend voor een project, maar moet je nu de diameter weten? Het kan lastig zijn, vooral als je geen direct meetlint bij de hand hebt. Gelukkig is er een eenvoudige manier om de diameter te berekenen alleen met de oppervlakte! Dit artikel helpt je stap voor stap, zonder ingewikkelde wiskunde.

Waarom de Diameter Belangrijk is

De diameter van een cirkel is een essentiële maat. Denk aan de volgende scenario's:

* Bouwprojecten: Je wilt een ronde tafel maken die perfect in een hoek past. * Engineering: Je ontwerpt een pijpleiding en moet de diameter van de buizen specificeren. * Dagelijks leven: Je koopt een pizza en wilt weten of hij in je oven past. * Wiskunde en wetenschap: De diameter is een belangrijke variabele in veel formules en berekeningen.

Kortom, de diameter helpt je om de grootte van een cirkel te begrijpen en te gebruiken in diverse toepassingen. Maar wat als je alleen de oppervlakte weet? Geen probleem, we gaan het oplossen!

De Formule: Oppervlakte naar Diameter

Hier is de basisformule die we gaan gebruiken. Begrijp deze goed, want het is de sleutel tot alles:

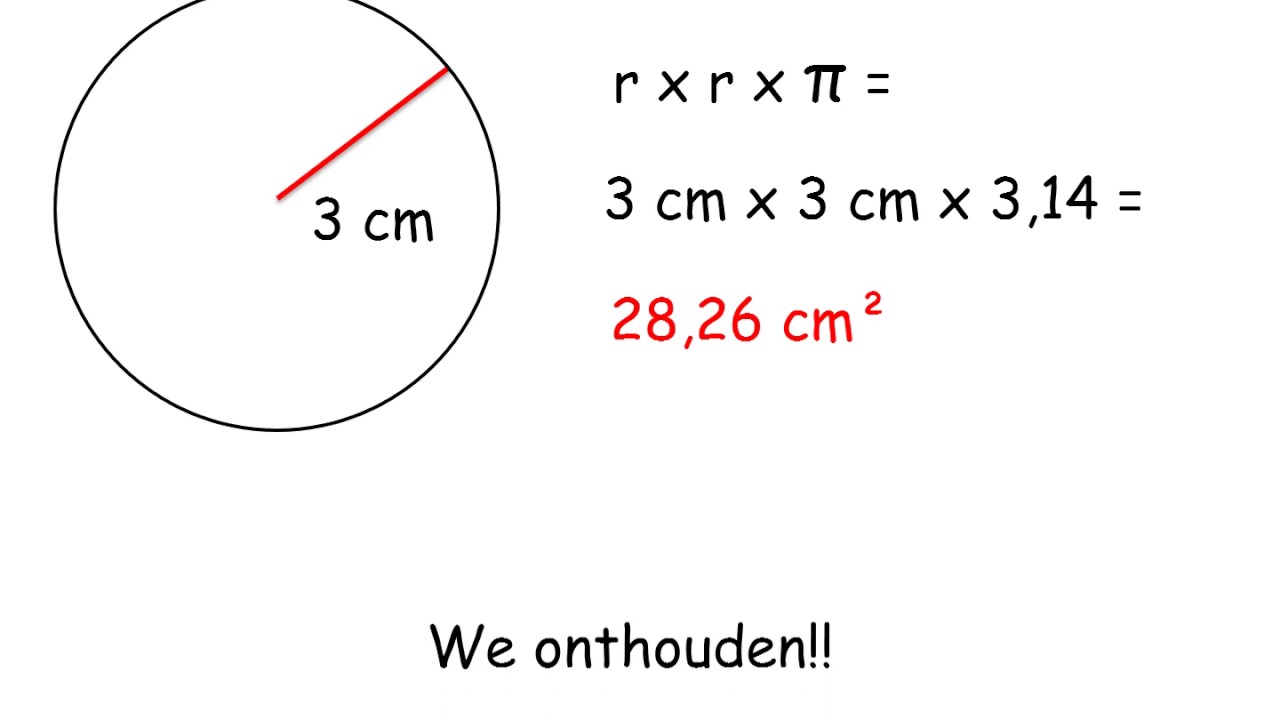
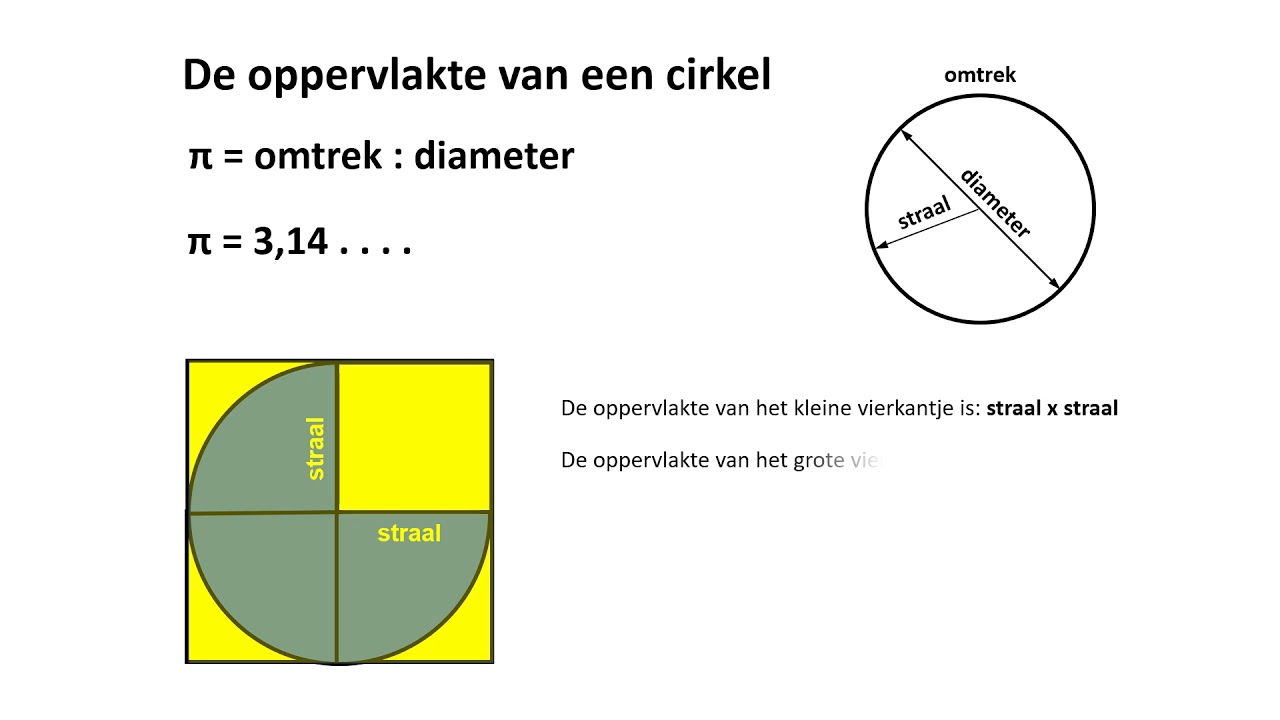
Oppervlakte (A) = π * r²

Waarbij:

* A = Oppervlakte van de cirkel * π (Pi) = ongeveer 3,14159 * r = Straal van de cirkel

Maar we willen de diameter (d) weten, niet de straal (r). We weten dat de diameter twee keer de straal is:

d = 2 * r

Dus, om de diameter te berekenen met de oppervlakte, moeten we deze formule omwerken. Hier is de stap-voor-stap uitleg:

Stap 1: Straal Berekenen

Om de straal (r) te vinden, moeten we de oppervlakteformule omschrijven:

r² = A / π

Nu nemen we de vierkantswortel van beide zijden:

r = √(A / π)

Stap 2: Diameter Berekenen

Nu we de straal (r) hebben, kunnen we de diameter (d) berekenen:

d = 2 * r

Dus:

d = 2 * √(A / π)

Dit is de formule die je nodig hebt!

Praktische Voorbeelden

Laten we een paar voorbeelden bekijken om het duidelijker te maken:

Voorbeeld 1: Een Pizzadoos

Stel, je hebt een pizzadoos met een oppervlakte van 600 vierkante centimeter. Wat is de diameter van de pizza?

Bereken de straal: r = √(600 / 3,14159) ≈ √(190,98) ≈ 13,82 cm
Bereken de diameter: d = 2 * 13,82 cm ≈ 27,64 cm

De diameter van de pizza is ongeveer 27,64 cm.

Voorbeeld 2: Een Ronde Tafel

Je wilt een ronde tafel maken met een oppervlakte van 2 vierkante meter. Wat moet de diameter van de tafel zijn?

Bereken de straal: r = √(2 / 3,14159) ≈ √(0,6366) ≈ 0,798 m
Bereken de diameter: d = 2 * 0,798 m ≈ 1,596 m

De diameter van de tafel moet ongeveer 1,596 meter zijn.

Tips en Trucs

Hier zijn een paar tips om het berekenen van de diameter makkelijker te maken:

* Gebruik een rekenmachine: Een rekenmachine met een vierkantswortelfunctie is essentieel. * Online calculators: Er zijn veel online cirkel diameter calculators beschikbaar. Zoek naar "cirkel diameter berekenen oppervlakte" op Google. * Rond af: Rond je antwoorden af op een redelijk aantal decimalen, afhankelijk van de precisie die je nodig hebt. Twee decimalen is meestal voldoende. * Wees consistent met eenheden: Zorg ervoor dat je dezelfde eenheden gebruikt voor de oppervlakte en de diameter (bijvoorbeeld, vierkante centimeters en centimeters, of vierkante meters en meters). * Controleer je antwoord: Als je eenmaal de diameter hebt berekend, kun je terugrekenen om te controleren of je antwoord klopt. Bereken de oppervlakte met de berekende diameter en kijk of je de oorspronkelijke oppervlakte terugkrijgt.

Veelgemaakte Fouten

Hier zijn een paar veelgemaakte fouten die je moet vermijden:

* Vergeten de vierkantswortel te nemen: Vergeet niet de vierkantswortel te nemen van (A / π) om de straal te vinden. * De straal vergeten te verdubbelen: Vergeet niet de straal te verdubbelen om de diameter te krijgen. * Verkeerde waarde voor π gebruiken: Gebruik een nauwkeurige waarde voor π (bijvoorbeeld 3,14159) in plaats van een afgeronde waarde (bijvoorbeeld 3,14). * Eenheden vergeten: Vergeet niet de juiste eenheden te gebruiken voor de oppervlakte en de diameter.

De Wetenschap Achter de Cirkel

De cirkel is een fascinerende vorm die al duizenden jaren wordt bestudeerd. De Griekse wiskundige Archimedes was een van de eersten die de waarde van π nauwkeurig benaderde. Zijn werk legde de basis voor veel van de formules die we vandaag de dag gebruiken. Interessant is dat π een irrationeel getal is, wat betekent dat het oneindig veel decimalen heeft zonder een zich herhalend patroon. Dit maakt de berekening van de oppervlakte en diameter van een cirkel een oneindig nauwkeurig proces.

Volgens een studie van de Universiteit van Cambridge is een goed begrip van geometrie, inclusief cirkels, cruciaal voor succes in STEM-velden (Science, Technology, Engineering, and Mathematics). De basisprincipes van geometrie worden in de dagelijkse praktijk gebruikt, van het ontwerpen van bruggen tot het ontwikkelen van nieuwe technologieën. Het beheersen van de basisformules zoals die voor de oppervlakte en diameter van een cirkel is dus essentieel voor wie een carrière in deze gebieden ambieert.

Conclusie

Het berekenen van de diameter van een cirkel met de oppervlakte is een eenvoudig proces als je de juiste formule kent en de stappen volgt. Door de formule d = 2 * √(A / π) te gebruiken, kun je de diameter van elke cirkel berekenen, zelfs als je alleen de oppervlakte weet. Dus, de volgende keer dat je een cirkel ziet en je de diameter wilt weten, hoef je niet te gokken. Je hebt nu de tools en de kennis om het zelf te berekenen!

Blijf oefenen met verschillende voorbeelden om je vaardigheden te verbeteren. Hoe meer je oefent, hoe sneller en nauwkeuriger je zult worden. Veel succes!