Groter Dan Kleiner Dan Tekens

De groter dan (>) en kleiner dan (<) tekens, ook wel bekend als ongelijkheidsymbolen, zijn fundamentele symbolen in de wiskunde en de informatica. Ze worden gebruikt om de relatieve grootte van twee waarden aan te geven. Hoewel ze eenvoudig lijken, spelen ze een cruciale rol in diverse contexten, van basale vergelijkingen tot complexe algoritmen en data-analyse.

Het Begrijpen van de Basisprincipes

Het is essentieel om te begrijpen hoe deze tekens werken. Het groter dan teken (>) geeft aan dat de waarde aan de linkerkant groter is dan de waarde aan de rechterkant. Bijvoorbeeld, 5 > 3 betekent dat 5 groter is dan 3. Het kleiner dan teken (<) geeft daarentegen aan dat de waarde aan de linkerkant kleiner is dan de waarde aan de rechterkant. Bijvoorbeeld, 2 < 7 betekent dat 2 kleiner is dan 7.

Verschillende Varianten: Groter Dan of Gelijk Aan en Kleiner Dan of Gelijk Aan

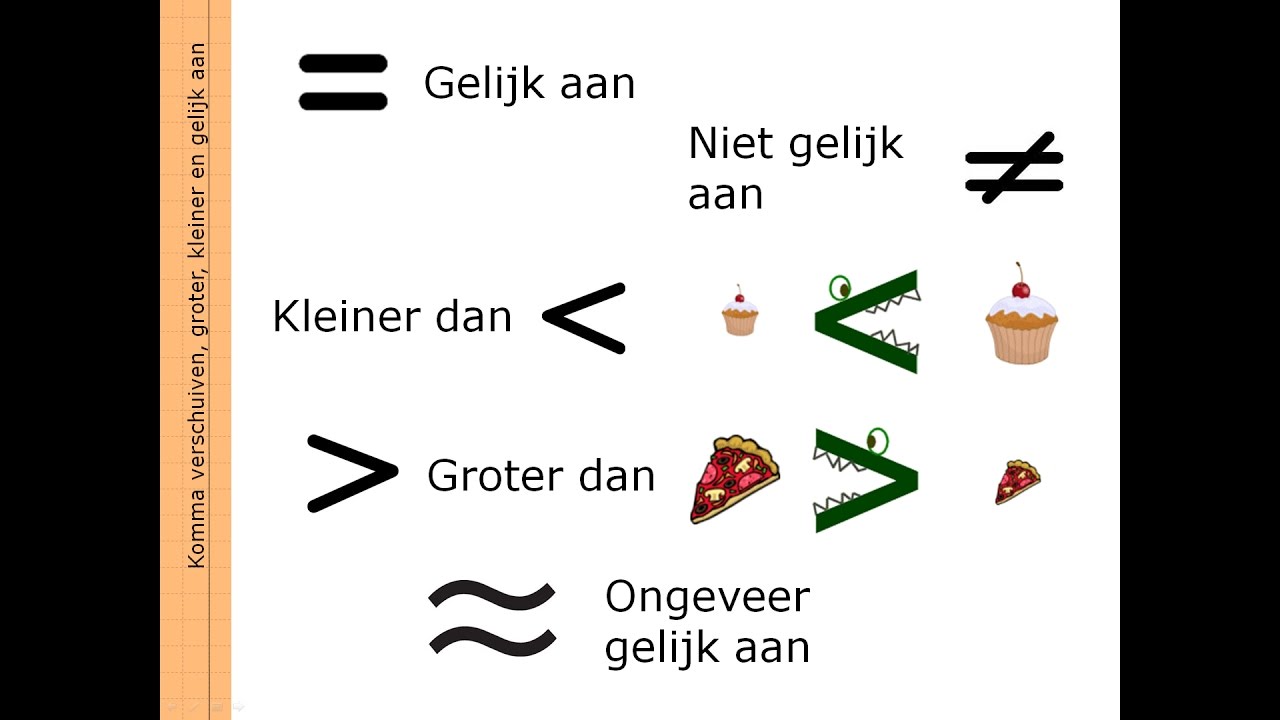
Naast de basisvormen bestaan er ook varianten die rekening houden met de mogelijkheid van gelijkheid. Het groter dan of gelijk aan teken (≥) geeft aan dat de waarde aan de linkerkant groter is dan of gelijk is aan de waarde aan de rechterkant. Het kleiner dan of gelijk aan teken (≤) geeft aan dat de waarde aan de linkerkant kleiner is dan of gelijk is aan de waarde aan de rechterkant. Deze varianten zijn belangrijk wanneer je niet zeker bent of de waarden exact gelijk zijn, maar je wel een relatie wilt specificeren.

Toepassingen in de Wiskunde

De groter dan en kleiner dan tekens zijn onmisbaar in de wiskunde. Ze worden gebruikt in:

Vergelijkingen en Ongelijkheden

In de algebra worden ongelijkheden gebruikt om een bereik van mogelijke waarden te definiëren voor een variabele. Bijvoorbeeld, de ongelijkheid x > 5 betekent dat x elke waarde kan aannemen die groter is dan 5. Deze ongelijkheden kunnen worden gecombineerd om meer complexe bereiken te definiëren, zoals 2 < x < 8, wat betekent dat x elke waarde kan aannemen tussen 2 en 8, maar niet 2 en 8 zelf.

Grafieken en Functies

Bij het grafisch weergeven van functies worden de groter dan en kleiner dan tekens gebruikt om domeinen en bereiken te definiëren. Bijvoorbeeld, als een functie alleen gedefinieerd is voor x > 0, dan betekent dit dat de grafiek van de functie alleen wordt weergegeven voor positieve waarden van x.

Calculus

In de calculus worden ongelijkheden gebruikt om de convergentie en divergentie van reeksen te bepalen. Ze spelen ook een rol bij het vinden van maxima en minima van functies en bij het bepalen van de intervallen waar een functie stijgend of dalend is.

Toepassingen in de Informatica

In de informatica zijn de groter dan en kleiner dan tekens eveneens essentieel. Ze worden gebruikt in:

Programmeren

In programmeertalen worden deze tekens gebruikt in voorwaardelijke statements (if-statements) en loops (while-loops, for-loops). Bijvoorbeeld, een if-statement kan controleren of een variabele groter is dan een bepaalde waarde voordat een bepaald codeblok wordt uitgevoerd. Een while-loop kan blijven lopen zolang een bepaalde voorwaarde (bijvoorbeeld, x < 10) waar is.

Databases

Bij het queryen van databases worden de groter dan en kleiner dan tekens gebruikt om records te filteren op basis van bepaalde criteria. Bijvoorbeeld, een SQL-query kan alle records selecteren waar de leeftijd groter is dan 25 of waar de prijs kleiner is dan 100.

Algoritmen

Veel algoritmen, zoals sorteeralgoritmen en zoekalgoritmen, maken gebruik van de groter dan en kleiner dan tekens om elementen te vergelijken en hun positie te bepalen. Bijvoorbeeld, een bubble sort algoritme vergelijkt steeds twee aangrenzende elementen en wisselt ze van plaats als ze in de verkeerde volgorde staan (bijvoorbeeld, als het eerste element groter is dan het tweede element).

Real-World Voorbeelden en Data

Om de relevantie van deze symbolen te illustreren, enkele concrete voorbeelden:

Financiën

In de financiële wereld worden de groter dan en kleiner dan tekens gebruikt om beleggingsrendementen te vergelijken. Bijvoorbeeld, als belegging A een rendement heeft van 8% en belegging B een rendement heeft van 6%, dan kunnen we zeggen dat het rendement van belegging A > het rendement van belegging B.

Gezondheidszorg

In de gezondheidszorg worden deze tekens gebruikt om bloeddrukwaarden te interpreteren. Een normale bloeddruk wordt vaak gedefinieerd als minder dan 120/80 mmHg. Dus, als iemands bloeddruk 130/90 mmHg is, dan is zowel de systolische als de diastolische druk > de normale waarden.

Klimaatwetenschap

In de klimaatwetenschap worden deze tekens gebruikt om temperatuurveranderingen te analyseren. Als de gemiddelde temperatuur in een bepaald jaar hoger is dan het gemiddelde over een langere periode, dan geeft dit een indicatie van opwarming van de aarde. Bijvoorbeeld, als de gemiddelde temperatuur in 2023 > het gemiddelde over de periode 1950-2000, dan is er sprake van een temperatuurstijging.

Data Analyse: Een Concreet Voorbeeld

Stel, je hebt een dataset met de verkoopcijfers van verschillende producten. Je wilt alle producten selecteren waarvan de omzet hoger is dan €1000. Met behulp van een programmeertaal zoals Python en de bibliotheek Pandas kan dit als volgt:

```python import pandas as pd # Voorbeeld dataframe data = {'Product': ['A', 'B', 'C', 'D'], 'Omzet': [500, 1200, 800, 1500]} df = pd.DataFrame(data) # Selecteer producten met een omzet > 1000 hoge_omzet_producten = df[df['Omzet'] > 1000] print(hoge_omzet_producten) ```

In dit voorbeeld wordt het groter dan teken (>) gebruikt om de rijen in het dataframe te filteren. Het resultaat is een nieuw dataframe met alleen de producten waarvan de omzet groter is dan €1000. Dit is een eenvoudige maar krachtige toepassing van de groter dan tekens in de data-analyse.

Belang van Correct Gebruik

Het is cruciaal om de groter dan en kleiner dan tekens correct te gebruiken. Een verkeerd gebruik kan leiden tot foutieve conclusies, verkeerde berekeningen, en in de informatica tot bugs in de code. Bijvoorbeeld, als je per ongeluk < gebruikt in plaats van >, dan kan je code een heel ander resultaat geven dan verwacht.

Daarnaast is het belangrijk om de context te begrijpen. In sommige situaties kan het nodig zijn om absolute waarden te gebruiken of om rekening te houden met foutmarges. Het simpelweg vergelijken van twee waarden met een groter dan of kleiner dan teken is niet altijd voldoende om een betrouwbare conclusie te trekken.

Conclusie

De groter dan en kleiner dan tekens zijn eenvoudige maar krachtige instrumenten die een cruciale rol spelen in de wiskunde, de informatica, en talloze andere disciplines. Een goed begrip van deze symbolen is essentieel voor iedereen die met cijfers, data, of algoritmen werkt. Of je nu een student bent, een programmeur, een data-analist, of een wetenschapper, het correct interpreteren en toepassen van deze tekens is van onschatbare waarde.

Oefen regelmatig met verschillende voorbeelden om je vaardigheid in het gebruik van de groter dan en kleiner dan tekens te verbeteren. Probeer verschillende soorten problemen op te lossen en test je kennis. Door consistent te oefenen, zul je een dieper begrip ontwikkelen en fouten voorkomen. Blijf leren en ontdek de vele toepassingen van deze fundamentele symbolen!