Hoe Bereken Je De Inhoud

Ben je ooit benieuwd geweest hoeveel ruimte er in een doos past, of hoeveel water er in een zwembad kan? Het antwoord ligt in het concept van inhoud, ook wel bekend als volume. Of je nu een student bent die worstelt met wiskunde, een huiseigenaar die een tuin wil aanleggen, of simpelweg iemand die graag wil begrijpen hoe de wereld om hen heen werkt, het berekenen van de inhoud is een essentiële vaardigheid. Deze gids is speciaal samengesteld voor jou, om je stap voor stap te helpen begrijpen hoe je de inhoud van verschillende vormen kunt berekenen, en de kennis toe te passen in je dagelijkse leven.

Wat is Inhoud (Volume)?

Inhoud, of volume, is de hoeveelheid ruimte die een driedimensionaal object inneemt. Het wordt gemeten in kubieke eenheden, zoals kubieke centimeters (cm³), kubieke meters (m³) of kubieke inches (in³). Stel je voor dat je een blokje hebt van 1 cm lang, 1 cm breed en 1 cm hoog. Dat is een kubieke centimeter. In wezen berekenen we hoeveel van die kleine blokjes er in een bepaald object passen.

Waarom is het Berekenen van Inhoud Belangrijk?

Het berekenen van inhoud is veel meer dan alleen een wiskundige oefening. Het is een praktische vaardigheid die je op veel verschillende manieren kan helpen:

• Huishouden: Bepalen hoeveel verf je nodig hebt om een kamer te schilderen, hoeveel water je in een aquarium moet gieten, of de juiste maat koelkast kiezen.
• Koken: Recepten vereisen vaak het meten van ingrediënten in volume-eenheden.
• Bouw en Constructie: Berekenen van de hoeveelheid beton nodig voor een fundering, of de capaciteit van een opslagtank.
• Logistiek: Bepalen hoeveel goederen in een container passen voor transport.
• Wetenschap: Het volume is cruciaal bij veel wetenschappelijke experimenten, bijvoorbeeld het meten van vloeistoffen en gassen.

Basisinzichten: Lengte, Breedte en Hoogte

De basis voor het berekenen van de inhoud ligt in het begrijpen van de drie dimensies: lengte, breedte en hoogte. Elke driedimensionale vorm heeft deze drie dimensies, en het is de interactie tussen deze dimensies die de inhoud bepaalt.

• Lengte: De langste afmeting van een object.
• Breedte: De afmeting die loodrecht staat op de lengte.
• Hoogte: De afmeting die verticaal omhoog gaat vanaf de basis.

Het Berekenen van de Inhoud van Verschillende Vormen

De formule die je gebruikt om de inhoud te berekenen, hangt af van de vorm van het object. Laten we eens kijken naar een paar veelvoorkomende vormen:

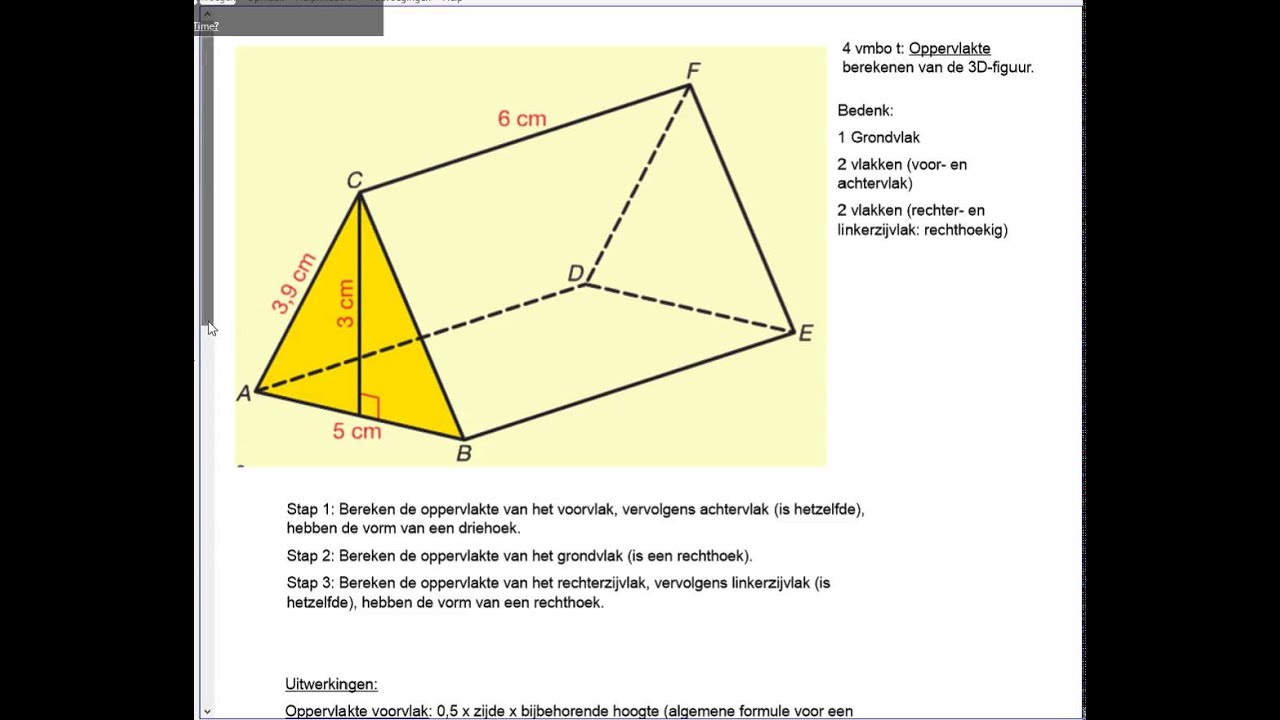
1. Kubus en Rechthoekig Prisma (Balk)

Een kubus heeft zes gelijke vierkante vlakken. Een rechthoekig prisma (of balk) heeft zes rechthoekige vlakken. De formule voor de inhoud van beide vormen is vergelijkbaar:

Inhoud = Lengte x Breedte x Hoogte

Voorbeeld: Een doos is 20 cm lang, 15 cm breed en 10 cm hoog. De inhoud is 20 cm x 15 cm x 10 cm = 3000 cm³.

2. Cilinder

Een cilinder is een driedimensionale vorm met twee parallelle cirkelvormige vlakken verbonden door een gebogen oppervlak. De formule voor de inhoud van een cilinder is:

Inhoud = π x r² x Hoogte

Waar:

• π (pi) ≈ 3.14159
• r is de straal van de cirkel (de helft van de diameter).

Voorbeeld: Een cilinder heeft een straal van 5 cm en een hoogte van 12 cm. De inhoud is 3.14159 x 5² cm² x 12 cm ≈ 942.48 cm³.

3. Bol

Een bol is een perfect ronde driedimensionale vorm, zoals een bal. De formule voor de inhoud van een bol is:

Inhoud = (4/3) x π x r³

Waar:

• π (pi) ≈ 3.14159
• r is de straal van de bol.

Voorbeeld: Een bol heeft een straal van 6 cm. De inhoud is (4/3) x 3.14159 x 6³ cm³ ≈ 904.78 cm³.

4. Kegel

Een kegel is een driedimensionale vorm die taps toeloopt van een cirkelvormige basis naar een punt. De formule voor de inhoud van een kegel is:

Inhoud = (1/3) x π x r² x Hoogte

Waar:

• π (pi) ≈ 3.14159
• r is de straal van de cirkel (de basis).
• Hoogte is de verticale afstand van de basis tot de punt.

Voorbeeld: Een kegel heeft een straal van 4 cm en een hoogte van 9 cm. De inhoud is (1/3) x 3.14159 x 4² cm² x 9 cm ≈ 150.80 cm³.

5. Piramide

Een piramide is een driedimensionale vorm met een veelhoekige basis en driehoekige zijvlakken die samenkomen in een punt (apex). De formule voor de inhoud van een piramide hangt af van de vorm van de basis. Voor een piramide met een vierkante basis:

Inhoud = (1/3) x Lengte Basis x Breedte Basis x Hoogte

Voorbeeld: Een piramide heeft een vierkante basis van 5 cm bij 5 cm en een hoogte van 8 cm. De inhoud is (1/3) x 5 cm x 5 cm x 8 cm ≈ 66.67 cm³.

Tips en Trucs voor het Berekenen van Inhoud

Hier zijn een paar handige tips om het berekenen van inhoud gemakkelijker te maken:

• Zorg voor consistente eenheden: Voordat je begint met rekenen, zorg ervoor dat alle afmetingen in dezelfde eenheden staan (bijvoorbeeld allemaal in centimeters of allemaal in meters). Zo niet, converteer ze eerst.
• Splits complexe vormen op: Als je een object hebt met een onregelmatige vorm, probeer het dan op te splitsen in eenvoudigere vormen waarvan je de inhoud wel kunt berekenen. Tel vervolgens de volumes van de individuele vormen bij elkaar op.
• Gebruik een rekenmachine: Vooral bij ingewikkelde formules is een rekenmachine een onmisbaar hulpmiddel.
• Controleer je antwoord: Neem even de tijd om je antwoord te controleren. Klinkt het logisch? Maak een ruwe schatting om te zien of je antwoord in de buurt komt.
• Oefening baart kunst: Hoe meer je oefent met het berekenen van de inhoud van verschillende vormen, hoe beter je er in wordt.

Praktische Toepassingen in het Dagelijks Leven

Laten we eens kijken naar een paar praktische voorbeelden van hoe je de inhoud kunt gebruiken in je dagelijkse leven:

• Je wilt een nieuw aquarium kopen: Je moet de inhoud van het aquarium kennen om te bepalen hoeveel water erin past en welke filters en pompen je nodig hebt.
• Je wilt een zwembad vullen: Je moet de inhoud van het zwembad kennen om te bepalen hoeveel water je nodig hebt en wat de kosten zullen zijn.
• Je wilt een taart bakken: Recepten geven vaak de grootte van de bakvorm aan. Je kunt de inhoud berekenen om te bepalen of je voldoende beslag hebt en of je de baktijd moet aanpassen.
• Je wilt verhuizen: Je kunt de inhoud van je dozen schatten om een idee te krijgen van hoeveel ruimte je nodig hebt in een verhuiswagen.

Van Theorie naar Praktijk: Oefeningen

Om je begrip te verdiepen, volgen hier een paar oefeningen:

1. Bereken de inhoud van een rechthoekige bloempot met een lengte van 30 cm, een breedte van 20 cm en een hoogte van 15 cm.
2. Bereken de inhoud van een cilindervormige beker met een straal van 4 cm en een hoogte van 10 cm.
3. Bereken de inhoud van een bolvormige kerstbal met een straal van 5 cm.

Conclusie: Inhoud Berekenen is een Krachtige Vaardigheid

Het berekenen van de inhoud is een waardevolle vaardigheid die je in staat stelt om de wereld om je heen beter te begrijpen en problemen op te lossen. Door de basisprincipes te begrijpen en te oefenen met verschillende vormen, kun je zelfverzekerd de inhoud van objecten berekenen en deze kennis toepassen in je dagelijkse leven. Dus, ga erop uit, meet, bereken en ontdek de ruimte!

We hopen dat deze gids je heeft geholpen om de basisprincipes van het berekenen van inhoud te begrijpen. Blijf oefenen en je zult versteld staan van wat je kunt berekenen!